
鍵盤楽器音楽の歴史(41)音律について
16世紀あたりまでは「鍵盤楽器の調律は1/4コンマ・ミーントーン」ぐらいの認識で十分だったのですが、17世紀も後半になると、そうも言ってられなくなります。ここはひとつ西洋音楽の音律理論を一からおさらいしてみましょう。
テトラコルド
中世ヨーロッパの大学では音楽は幾何学や天文学などと並ぶ自由七課の1つに数えられていました。そこで教えられていたのはもちろん古代ギリシャの音楽理論です。
まず基本的な音程について。
楽器の弦を、張力を同じまま長さを半分にすると、音の周波数は2倍になります。これは音高がオクターヴ Diapason の音程だけ高くなることを意味します。
しかし古代ギリシャの音階はオクターヴではなく、完全4度 Diatessaron の音程を基礎としていました(例:ドから下のソまでの音程)。これは周波数比 4:3 の音程であり、つまり楽器の弦の長さを張力を同じままに、その1/3に相当する長さだけ追加すれば完全4度低い音になります。
逆に1/3短くした場合、周波数比 3:2 となり、完全5度 Diapente 高い音になります(例:ドから上のソまでの音程)。
オクターヴはもちろん、完全4度や完全5度離れた音も、同時に鳴らすと非常に良く協和します。これは周波数比が単純な整数比であるため、双方の倍音列が良く重なるためです。
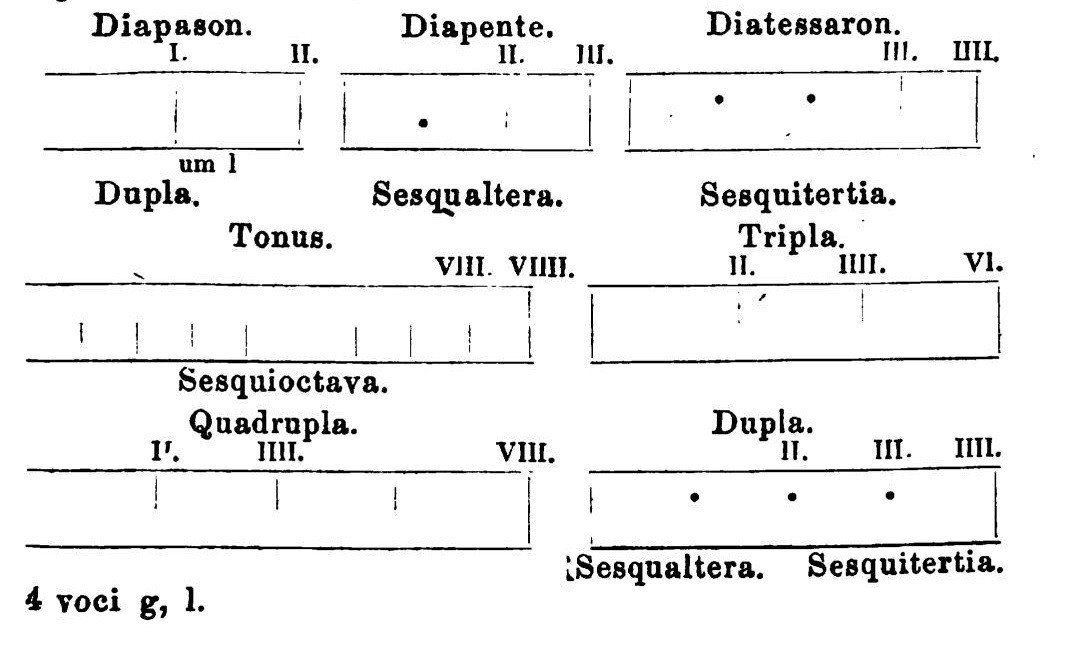
Boethius, De institutione musica, ed. Gottfried Friedlein, 1867.
では古代ギリシャの竪琴を想像してみてください。
こんなのです。

Terracotta amphora, ca. 490 B.C.
https://www.metmuseum.org/art/collection/search/254896
このような楽器に、まず2本の弦を完全4度の音程になるように張ります。そしてその間にさらに2本の弦を張って4つの音による音階を作ります。これをテトラコルドと呼び古代ギリシャの音楽理論の基礎となるものです。
テトラコルドは3つの種類(ゲノス) に分けられます。ディアトノン、クロマティコン、エンハルモニオンです(ラテン語なら Diatonum, Chromaticum, Enarmonium)。
ディアトノンのテトラコルドの場合上から全音・全音・半音となるように分割します。クロマティコンは三半音(短3度)・半音・半音、エンハルモニオンは二全音(長3度)・ディエシス・ディエシス、となります(ディエシスは半音以下の微小音程)。
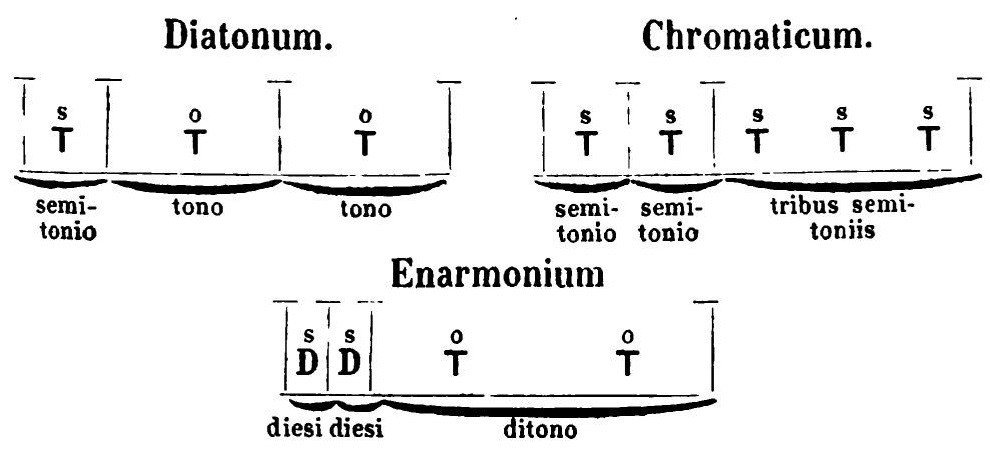
Boethius, De institutione musica, ed. Gottfried Friedlein, 1867.
ここで全音だの半音だのが具体的にどんな大きさの音程なのか?という疑問が当然出てくると思いますが、古代ギリシャにおける実践ではどうも数比などにはよらず適当に雰囲気でやっていたようです。両端の完全4度の枠組みは絶対のものですが、間の2音については厳密に定めることはせず、むしろそれによって微妙な「陰影」が生じることが重要だったようです。
ピタゴラス学派は数学的に音楽を研究し、アルキタス (428-347 BC) は数比によるテトラコルドの分割を示しましたが、実用されたものとは思われません。その分割比は以下のようなもので、やはり音程の大きさは不均一です。誤解されがちですが、いわゆる「ピタゴラス音律」は古代ギリシャの音律ではありません。
Diatonic: 28/27, 8/7, 9/8
Chromatic: 28/27, 243/224, 32/27
Enharmonic: 28/27, 36/35, 5/4
全音階
テトラコルドから完全音組織(システマ・テレイオン)が作られます。
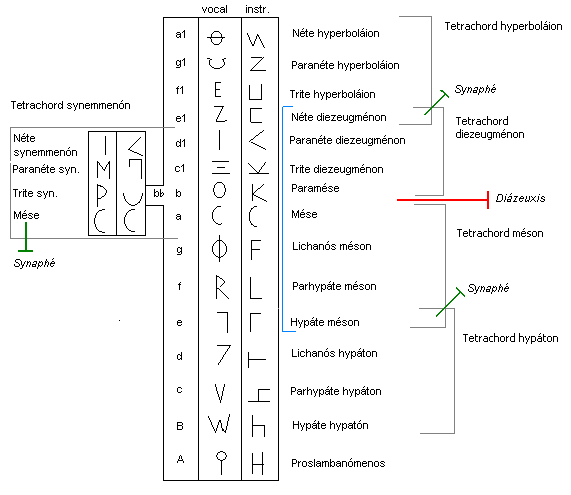
https://commons.wikimedia.org/wiki/File:Systema_teleion.png
まず基本となるテトラコルドの下に、1音重なる形でもう一つのテトラコルドを連結して七音の音階が作られます。
そして基本のテトラコルドの最高音である「メセー」の上に、全音の間隔をあけて同じ様に連結したテトラコルドを配置します。この時メセーと上の連結テトラコルドの最高音「ネーテー・ヒュペルボライオーン」はオクターヴの音程になります。
さらに下の連結テトラコルドの下に、全音の間隔をあけてテトラコルドに属さない「プロスランバノメノス」という音を配置します。この全部で2オクターヴの音階が大完全音組織です。これをディアトノンのテトラコルドで作ったものは現在のピアノの鍵盤の白鍵と同じ音程配列となります。すなわちこれが全音階の起源です。階名で「ラ」の音が「A」であるというのは、このメセーに由来しています。
またメセーの上に隙間を開けずにテトラコルドを重ねて連結したものは小完全音組織です。ディアトノンのテトラコルドの場合、音階にB♭が現れます。

http://tonalsoft.com/enc/p/pis.aspx
大完全音組織は2オクターヴに渡る音階で、各音が固有の名称を持ちます。古代ギリシャの音名はオクターヴではなくテトラコルドに基づくものであるため、オクターヴ違いの音の名前に関連性はありません。なおクロマティコンやエンハルモニオンのテトラコルドを用いた完全音組織では、ディアトノンとは全く異なる音階が得られますが、それでも音名は変わりません。まことに理不尽ですが、クロマティコンやエンハルモニオンはローマ帝国時代に廃れてしまい、以後の説明には出てこないのでご安心ください。
全音階の音名を7つのアルファベットで表し、オクターヴ違いの音にも同じアルファベットを割り当てるようになったのは、11世紀の偽オドやグイード・ダレッツォの頃からのようです。またモノコードを使って音階を説明するにあたり、かつてのプロスランバノメノスであるAの全音下に開放弦の音である Γ(ガンマ)が加えられました。

Codex Lat. 51, f. 35v.
ヘクサコルドによるソルミゼーションもグイードの発案といわれ、これに後に「シ」が加わって現在の階名となります。

ピタゴラス音律
グイードが著書《ミクロログス》(1026) で説明しているのは、いわゆるピタゴラス音律で、ご存知のようにオクターヴと完全4度と完全5度で全音階を定義するものです。
下図の左側は完全4度、中央はオクターヴ、右側は完全5度の関係を示しています。これを例えば以下のように巡れば全音階のピッチクラスを揃えられます。
f -4 → C +oct → c -4 → g -4 → D +5 → a +5 → e -4 → b
これと同様の方法が中国や日本では三分損益法と呼ばれ、古くから用いられてきました。ヨーロッパでもこれで向こう300年ほどは問題ありませんでした。

Cod. Bodmer 77, f. 3r.
時代は下って14世紀、現存最古の鍵盤音楽曲集であるロバーツブリッジ写本の音楽は、すでに現代と同じ1オクターヴに12音を備える半音階の鍵盤を要求します。こうなると問題が出てきます。
オクターヴ違いの音にも同じ音名を当てることにしましたが、完全4度(4/3)や完全5度(3/2)はオクターヴ(2/1)とは素であるため、完全4度や完全5度の冪乗からオクターヴの音程を導出することは原理的に不可能です。
したがって C から12回完全5度上昇した B♯ は、元の C から7オクターヴ上の C とは一致せず、531441/524288 ≒ 23.5 cents のズレが生じます。これをピタゴラス・コンマと呼びます。半音の1/4程度の音程です。このピタゴラス・コンマを発見したのはフィロラオス (c. 470-c. 385 BC) であるとされています。
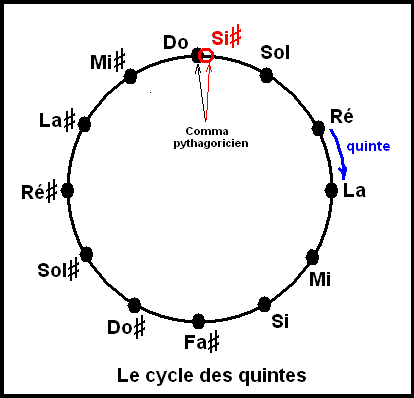
https://commons.wikimedia.org/wiki/File:Comma_ditonique.PNG
オクターヴにこだわらずどんどん新しい音名を作っていけば問題はありませんが、鍵盤のキーの数は限られているので妥協が必要になります。前述の例で B♯を C で代用した場合、E♯から C への音程は正しい完全5度よりもピタゴラスコンマだけ狭い音程になります。この音程は協和せず酷い響きになるため狼の声に擬えてウルフの5度と呼ばれます。
1オクターヴに12音の鍵盤楽器をピタゴラス音律で調律した場合、ウルフの5度が生じるのは避けられませんが、場所は五度圏上で好きに選べるので、なるべく使わない音程に押し付けます。
1479年頃のウルビーノのドゥカーレ宮殿の寄木細工で作られたクラヴィコードの絵は、フレッティングの解析の結果 B–F# 間にウルフを持つピタゴラス音律で調律されているようです。

ミーントーン
ピタゴラス音律には他にも問題があります。15世紀にはイングランドのフォーブルドンなどの3度、6度の和音を多用する楽曲が大陸の音楽に影響を与えます。ルネサンス音楽の始まりです。
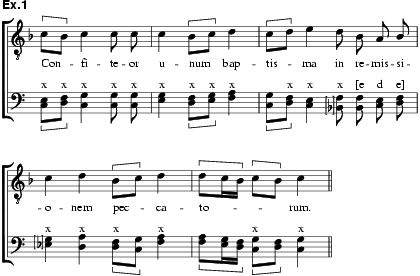
ピタゴラス音律の長3度(ド-ミ)は 81/64 (≒ 408 cents)というやや複雑な比率で、和音はきつい響きになります。なので長3度は「不完全協和音程」に分類されていましたが、長3度の和音を合唱で歌う際には、近似のより単純で協和する 5/4 (≒ 386 cents) の音程が自然に選択されます。この良く協和する「ピュア(純正)」な長3度 5/4 と、ピタゴラス音律の長3度 81/64 の差、 81/80 ≒ 21.5 cents をシントニック・コンマと呼びます。
歌唱であれば臨時に純正な長3度を使うのに何の問題もありませんが、音高の固定した鍵盤楽器ではそうもいきません。12音の半音階で全ての3度と5度を同時に純正にすることは原理的に不可能です。ウルビーノの例を見る限り15世紀後半になっても鍵盤楽器にピタゴラス音律が使われていたようですが、教会のオルガンで合唱と共に演奏する場合など、どうしても問題がでてきます。これに対する解決策がミーントーン・テンペラメント(中全音律)です。テンペラメントとは音程をあえて少しずらす調律法のことです。
長3度はピタゴラス音律では4つの完全5度の連鎖から導出されます(直接的に導出されるのは17度=2オクターヴ+長3度)。例えば C に対する E は、C-G-D-A-E という5度の連鎖によって求められます。
つまり完全5度を狭くすればその4倍も長3度が狭まります。ピタゴラス音律の長3度が純正な長3度よりもシントニックコンマ分広いことが問題になっているのですから、完全5度をそれぞれ1/4シントニックコンマ狭くすれば長3度が純正になります。これが1/4コンマ・ミーントーンの原理です。
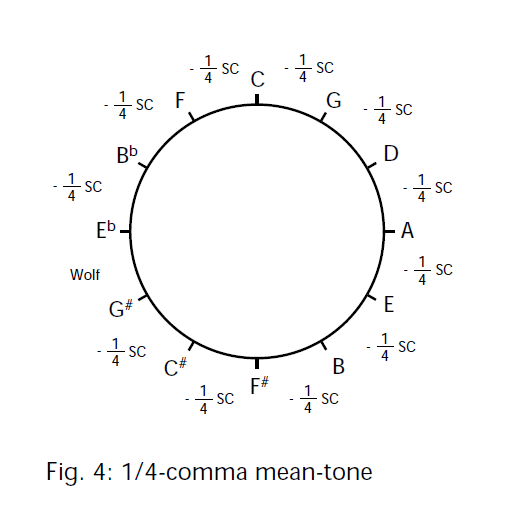
Reprinted from "A Passable and Good Temperament," Johan Norrback (2002).
1/4シントニックコンマ狭い5度は少々透明感に欠けますが、我慢できる範囲内です。それよりも合唱において合わせづらい3度音程をオルガンでリードできるメリットは大きかったでしょう。
しかし代償は他にもあり、ピタゴラス音律とは逆に約737セントと非常に広いウルフの5度が生じるため、使用できる調が著しく制限されます。
ピタゴラス音律のウルフの5度は純正音程よりも狭かったので、これによって導出される長3度も狭くなって、むしろ純正に近づくので好都合だったのですが、ミーントーンではそのような恩恵はありません。ウルフの5度から作られる3度音程も酷い響きになります。1/4コンマ・ミーントーンで演奏可能な調は、一般に調号3つが限界とされ、それすらも普通は使われません。
またミーントーンではピタゴラス音律とは全音階的半音(リンマ)と半音階的半音(アポトメ)の大小関係が逆転します。つまりピタゴラス音律では B-C 間の半音よりも C-C♯ 間の半音が広かったのですが、ミーントーンでは B-C の方が広くなります。これはミーントーンでは一般に導音が広めになることを意味し、旋律的にはいささか不利になります。
この1/4コンマ・ミーントーンはピエトロ・アーロンが《Thoscanello de la musica》(1523) で言及したのが初出とされ、「アーロンのミーントーン」などと称されたりもしますが、実際の所アーロンは「長3度を純正にする」という程度のことを示唆しているに過ぎません。

1/4コンマ・ミーントーンに関する数学的な説明は ジョゼッフォ・ツァルリーノの《Le Dimostrationi Harmoniche》(1571) を待つことになります。しかしその頃にはミーントーンはとっくにデファクトスタンダードになっていました。
ミーントーンの実践自体は早くも15世紀に始まると見られ、コンラート・パウマン (c.1410-1473) のオルガン曲にみられる3度音程の多用はミーントーンの調律を前提にしたものだと考えられています。

ところで1/4コンマだけがミーントーンではありません。ツァルリーノは1/4コンマ・ミーントーンよりも先に《Le istitutioni harmoniche》(1558) で2/7コンマ・ミーントーンについて解説しています。5度を狭める量が2/7コンマの場合は純正長3度は得られませんが、長3度と短3度が同じだけ純正に近づきます。フランシスコ・デ・サリーナスが《De musica libri septem》(1577) で論じた1/3コンマ・ミーントーンは短3度が純正になります。さすがに1/3コンマも5度をいじると悪影響は避けられず、提唱者本人ですら音が暗いと言っているので実用性に難ありですが。
完全5度を狭くする量を減らし、1/5、1/6コンマなどとした場合は、3度が純正にならない代わりにウルフが小さくなって使える調が増えます。 J.S.バッハと同時代のオルガン製作者、ゴットフリート・ジルバーマン (1683-1753) は1/6ピタゴラスコンマ・ミーントーンを使用していました。

Norrback (2002)
平均律
完全5度を狭くする量をさらに減らした1/12ピタゴラスコンマ・ミーントーンがすなわち平均律 Equal temperament です。

Norrback (2002)
平均律ではピタゴラスコンマが均等に全ての5度に分散されることになるため、ウルフが消滅し、全ての調が同様に使用できるようになります。つまり平均律は1オクターヴを均一な半音(100セント)で等分割した音律であるともいえます。
しかし平均律の長3度の大きさは400セントで、純正長3度の約386セントには程遠いため、長3度の響きはよくありません。一方、完全5度は700セントで純正な完全5度の約702セントと遜色なく、ほぼ純正と言っていい完全5度が使えます。つまるところ平均律の音響的な性質はピタゴラス音律に割と近いと言えます。
正確に平均律を割り出すには2の12乗根の計算が必要になり、それは明の朱載堉の《律学新説》(1584) やマラン・メルセンヌの《Harmonie universelle》(1636) などで算出されるわけですが、実践においてはそのような厳密な数値は重要ではありませんでした。どうせ無理数ですしね。

最初に平均律が普及したのは鍵盤楽器ではなく、リュートやギターといったフレット楽器においてです。平均律には調律の手がかりとなる純正な音程がオクターヴを除けば皆無なので調律は大変ですが、フレット楽器の場合は、ヴィンチェンツォ・ガリレイが 《新旧音楽の対話》 (1581) で述べているように、半音を 18/17 (≒ 99 cents) とすることで実用的には十分すぎる精度で平均律を近似できます。
そもそも直線のフレットを用いるならば半音の大きさが一定である平均律が最も自然な音組織だといえます。平均律の実践は、数学者の理論とは別に、楽器奏者たちが良い塩梅のフレット位置を手探りで探究する中で見出されたものかと思われます(当時のフレットは単にネックにガットを巻いたものなので簡単に調節できました)。ホアン・カルロス・アマートの《Guitarra española》(1586) にある24の調によるパセラの例もあり、16世紀後半にはフレット楽器に平均律が一般化していていたと考えられます。ただし補助フレットなどによって純正音程に近づける工夫をする奏者もいたようです。
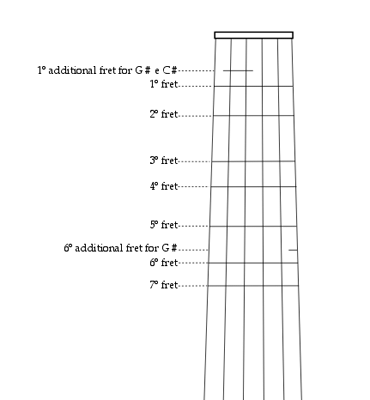
https://www.modoantiquo.com/temperatur/temperatur_desc_en.html
フレスコバルディがオルガンを平均律で調律しようと言い出して騒ぎになった話を紹介しましたが、鍵盤楽器では平均律はなかなか普及しませんでした。
実際17世紀にもなれば平均律は広く知られており、鍵盤楽器に適用するのにもさほど技術的な障害はありませんでした。例えば幾何学的に作図したテンプレートをモノコードに貼って、それで1音づつ対照しながら調律していくという方法なら音律の原理が何であれ関係はありません。今の私達がデジタルチューナーで調律するようなやり方です。
当時の鍵盤奏者やオルガン建造家に平均律が受け入れられなかったのは、その3度の響きの悪さに加え、調性格が失われるということが理由の一つです。平均律での移調や転調というのは基準ピッチを半音単位で上下することでしかありません。しかしミーントーンなどの不等分な音律では、ピッチとは別に調ごとに固有の性格があり、当時の音楽家はそれを重要視していたのです。
17世紀のオルガニストにして音楽理論家であるアンドレアス・ヴェルクマイスター (1645-1706) は1697年の著書《Hypomnemata Musica》でこう述べています。
もし、あらゆる半音、全音、3度、5度などが同じ数のうなりをもっているなら、移調によって得られる喜びはわずかでしか無いだろう。例えばDから始まるドリア旋法がCかEに2度移高されたとすると、そうした移調は著しい変化と興奮を呼び起こす。音高を変えるだけでは全音と半音を並べ換えたり協和音程のうなりを変えたりした場合ほどの効果は生じない。
一方で平均律の移調・転調が自由である利点は大きいことも事実です。しかしそのためには別に平均律でなくとも要はウルフを無くせばいいのです。そのために様々な鍵盤楽器の調律法が考案されました。
ヴェルクマイスター
そうした不等分ながら全ての調で演奏可能な「サーキュレイティング・テンペラメント」の代表例がヴェルクマイスター第3法です。これはアンドレアス・ヴェルクマイスターの《Musicalische Temperatur》(1691) で解説されている鍵盤楽器の調律法で、ブクステフーデやJ.S.バッハなどの17~18世紀のドイツの鍵盤音楽によく適合します。

この書で扱われている調律法は6つあるのですが、第1法は純正律、第2法は1/4コンマ・ミーントーンで、ただの前説に過ぎず、第4、5、6法は現在はほとんど使われることがありません。なお第6法はモノコードを196分割する特殊な方法で記述されています。

ヴェルクマイスター第3法はピタゴラスコンマを4分割し、C-G、G-D、D-A、B-F♯ の4つの5度をそれぞれ1/4ピタゴラスコンマ狭め、他の5度を純正にするものです。これによってウルフが無くなり、あらゆる調で演奏可能になります。
さらによく使う白鍵が主体の調では5度が狭められているため、3度が純正に近づきます。黒鍵の多い調では3度が純正から外れていきますが、最悪でもピタゴラス音律と同じになるだけなので十分演奏に耐えます。


Norrback (2002)
ヴァロッティ
ヴェルクマイスター第3法と並んで、現在オルガンやチェンバロの調律によく使われているのがヴァロッティ・テンペラメントです。これは18世紀イタリアのフランチェスコ・アントニオ・ヴァロッティ (1697-1780) による《近代音楽の理論的及び実践的な科学》の第2巻に記述されている調律法ですが、彼の生前には第1巻までしか出版されておらず、草稿のまま保存されていたものが全て出版されたのは、漸く1950年のことです。
この方法ではコンマを6分割して五度圏の半分 F-C、 C-G、 G-D、 D-A、 A-E、 E-B の6つの5度を1/6コンマ狭くし、残りの半分の5度を純正にするものです。これにより白鍵側では1/6コンマ・ミーントーン風、黒鍵側ではピタゴラス音律風になります。
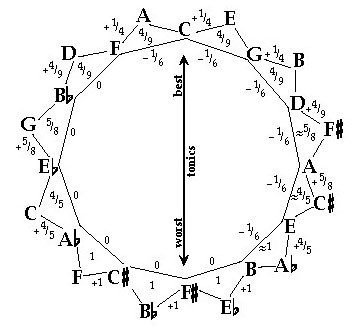
ここで6分割するコンマはヴァロッティの原著ではシントニックコンマを用いているのですが、これではウルフの原因であるピタゴラスコンマをきっちり相殺できず具合が悪いので、現代ではピタゴラスコンマを用いるヴァリアントが一般的です。
このピタゴラスコンマ版のヴァロッティは、トマス・ヤング (1773-1829) が提案した調律法、ヤング第2法と割り振りが少し違うだけで、ほぼ同じものになります(狭い5度の範囲が五度圏で1つずれる)。
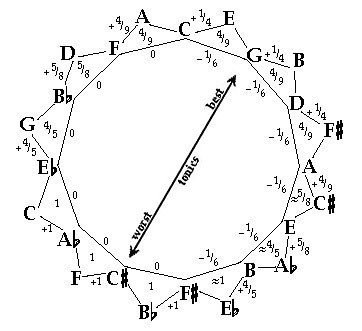
ヴァロッティ・テンペラメントは五度圏の半分づつというシンプルな分け方でわかりやすく、音質も優れていることから、現在では非常に人気のある調律法ですが、20世紀後半に再発見されるまでは使用された形跡に乏しいため、歴史考証を重視したバロック音楽の演奏などで使用するのは些か躊躇われます。

フランス式調律法
一方、フランスではテンペラメントを厳密な数値ではなく感覚的な言葉で説明していました。ジャン・フィリップ・ラモーの《音楽理論の新体系 Nouveau système de musique théorique》(1726) で説明されている調律法はこのようなものです。
クラヴサンのオクターヴ内の割り振りに関しては、初めのいくつかの5度をいくらか狭くするのが慣習的である。4つ目の5度を調律したら確認としてその音と長3度をなす出発音と比較する。もしその長3度が耳の要求する純正さを得ていなければ初めに戻り各5度をもう少しづつ狭くする(中略)割り振りの中央まで来たら5度は少し純正に戻し、最後の5度まで段階的にそのようにしてゆく。
非常にふわふわした説明で解釈の余地が大いに残されていますが、要するに1/4コンマ・ミーントーンをベースにして、ウルフを1つの5度に集中させずにグラデーションをもって拡散させたものと考えられるでしょう。

桒形亜樹子 (2009)「不等分か等分か?ーフランス18世紀音律の色彩、その曖昧さの魅力」より転載
他にもダランベールやルソーなどが似たような方法を記述しており、現在ではこれらのフランス流の鍵盤楽器調律法を総称してテンペラメント・オルディネール Tempérament ordinaire と呼びます。これは平均律に対して「通常の」調律法として説明されたことに由来します。これらの調律法では全ての調が使えるとまではいきませんが、実用的に十分な範囲の調に対応できます。
ラモーはこのように説明を続けています。
最後の3つの5度および最後の4つ、あるいは5つの長3度が純正音程よりも広くなるのは許容できる。なぜなら、そのような差は、ほとんど感知できないのみならず、より激しい表現のために使われる場合を除けば、まれにしか使われない転調でのみ生じるからである。だから諸音程の異なる変化に応じて、諸音程から様々に異なる印象を受ける、ということに注目すべきである。例えば経験から知っているように、自然なままの純正長3度には喜びを感じ、広げられた場合は激しい怒りの印象さえ受けるのである、そして自然なままの純正短3度に甘美と優しさを感取し、狭められた場合は憂鬱になる。聡明な音楽家ならば諸音程の持つこうした様々な効果をどのように利用するのか知っているし、そうして引き出した表現によって非難されかねない音程の変化に価値を置くのである。
しかしラモーは1737年の著書《和声の生成 Génération harmonique》では手のひらを返して平均律を支持します。

音律によって旋法が移高された場合に生じる差異がそれぞれ異なる印象をもたらし、その印象が各旋法の性格を際立たせより一層の多様性を引き出すと考えている人がいる。しかしそれは誤りである。多様性の感覚は様々な調の絡み合いから生じ、決して音程の変化から生じるのではない。音程の変化は単に聴覚に不快感を与え、聴覚は散漫になり正しく働かなくなるのである。
ラモーは具体的な平均律の調律手順についても説明しています。
5度を純正に合わせ、それからごくわずか狭める、これを次々と行う。
音が高すぎたり低すぎたりすると耳は正確に判断できないため、鍵盤の中央から始めるべきである。
どのくらい5度を狭くするかと言うと、まだそれらがほとんど純正であるかのように、つまり限りなく少なく、普通使われているものよりずっと少なくする。
以後フランスでは平均律はラモーの名とともに語られることになります。
キルンベルガー

18世紀のドイツでは、フリードリヒ・ヴィルヘルム・マールプルク (1718 -1795) が平均律を擁護していましたが、J.S.バッハの門人であるヨハン・フィリップ・キルンベルガー (1721-1783) は過激な平均律反対派で、著書《純正作曲の技法 Die Kunst des reinen Satzes in der Musik》(1771) で独自のテンペラメントを説いています。
https://en.wikipedia.org/wiki/File:Temp%C3%A9rament_de_Kirnberger_II.PNG
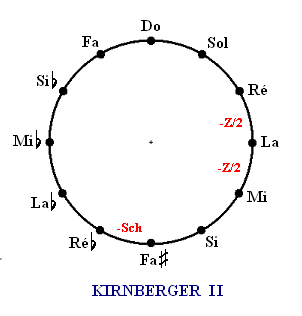
これは現在キルンベルガー第2法と呼ばれているもので(第1法は事実上単なるピタゴラス音律)D-A、A-E の5度を1/2シントニックコンマ狭め、残りのスキスマ(ピタゴラスコンマとシントニックコンマの差、約1.95セント)を F♯-C♯ から引いたものです。
この方法ではハ長調の三和音 C-E-G が純正になりますが、よりによって D-A と A-E という頻用する5度が酷く狭くされてしまっています。純正音程を実現するという理念優先の方式で、実用性にはかなり問題があるのですが、《純正作曲の技法》が定番の音楽理論書として広く読まれたため、それなりに普及したようです。歴史的にキルンベルガーの調律法といえばこれを指します。
当然ながらこれには批判が出たため、1779年のヨハン・ニコラウス・フォルケルへの手紙の中でキルンベルガーが代わりに提案したのがキルンベルガー第3法です。
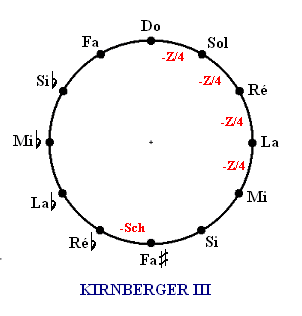
https://en.wikipedia.org/wiki/File:Temp%C3%A9rament_de_Kirnberger_III.PNG
キルンベルガー第2法の1/2コンマ狭い5度2つを、1/4コンマ狭い5度4つに変更したものです。ヴェルクマイスター第3法の出来損ないのようなテンペラメントですが、全ての調で支障なく演奏でき、さらに C-E の長3度が純正で調律がしやすいため、現代ではしばしば用いられています。しかしこの手紙が出版されたのは1871年のことであり、歴史的に使用された可能性が低い調律法であることには注意が必要です。
18世紀にはその他にも有象無象の鍵盤調律法が提案されましたが、うるさがたの批判をよそに結局シンプルな平均律が受け入れられていきました。
一方、教会ではかなり後までもミーントーンによる調律が残り、とりわけ保守的なイギリスでは教会のオルガンが平均律で調律されるようになるのは1851年のロンドン万博以降のことです。
