
数学(2022/5/26):キューネン本2冊についての記事_6.ZFC集合論の公理のリスト_4(中間生成物:順序数としての自然数)
(2022/6/15 19:00頃)(広義の)函数の記述を『整列可能集合』の記事に移動
1.ZFC集合論の公理のリストから中間生成物を構成する(続き)
1_1.全射、単射、全単射
前回は、
「何らかの一里塚を持つ(狭義)全順序集合」、『整列順序』と、
「整列順序に使われる集合」、『整列可能集合』まで定義したのでした。
これらは便利なのですが、バラツキがあり、目盛りとして使うには心もとありません。
バラツキのない「特別な整列順序」や、その「整列可能集合」があれば嬉しい訳です。
こうした「特別な整列順序における特別な整列可能集合」、「順序数」と呼ばれるものを、今回構築します。
***
そのために、「(広義の)函数」の考え方として、「全射」「単射」「全単射」の話をします。
***
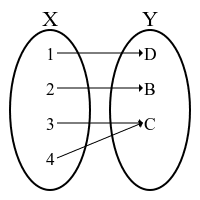
「(広義の)函数」における「始域」と「終域」の対応の仕方には4パターンあります。
「始域の全ての要素が終域の全ての要素に対応し、しかも始域の要素の別々のもの同士が終域のとある同じ要素に集中して対応しているとき」
このような(広義の)函数を「全射」と呼びます。
図を書くと分かりますが、これは
「始域が終域以上のある種の大きさを持つ」
と見立てられそうに見えます。
(集合の大きさの数、『濃度』や、それを一番正確に表す数、『基数』については、もう少し後で説明します)
(この画像は、2022/5/26現在、Wikipediaの「全単射」のページ由来のものです。以下同文)
***
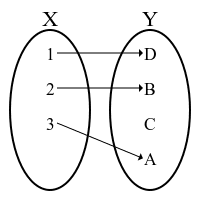
「始域の全ての要素が終域の全てではない要素に対応しているとき」
このような(広義の)函数を「単射」と呼びます。
図を書くと分かりますが、これは
「始域が終域以下のある種の大きさを持つ」
と見立てられそうに見えます。
***
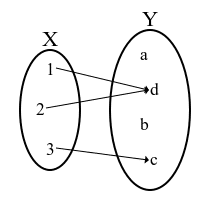
「始域の全ての要素が終域の全ての要素に対応し、しかも始域の別々の要素に終域の別々の要素が必ず一つだけ対応しているとき」
このような「完全に対応している」(広義の)函数を「全単射」と呼びます。
全射と単射の要素をいいところどりしたような性質なので、こう呼ばれることはまあ分かります。
そして、図を書くと分かりますが、これは
「始域と終域が同等のある種の大きさを持つ」
と見立てられそうに見えます。
なお、今回の記事で、これを使うことになります。

***
あとはこれらのいずれでもないようなタイプの「(広義の)函数」がたくさんあります。今回その話はどうでもいいので致しません。
1_2.順序数いろいろ
1_2_1.順序数
1_2_1_1.順序数の一般的な定義
1_2_1_1_A(成果物の下準備1_A).(所属による)推移的集合
いろいろな順序の内容に着目すると、その順序が所属(あるものはあるものの要素である)によって成り立っている場合や、包含(あるものはあるものの部分集合である)によって成り立っている場合があります。
***
さて、「所属していることによるある種の順序」と「包含されていることによるある種の順序」が同等となる特殊な集まりを考えることもできます。
実は、集まりの要素がまた集まりであることと、つまり所属によって推移性が成り立っていることにより、これが達成できます。
つまり、集まりの要素の要素もまた集まりであり、そのまた要素もまた集まりであり、という感じです。
推移性を満たす、推移関係を持つ集まり、『推移的集合』のうち、このような所属によって推移性を果たしているもの「を」、特別に『(所属による)推移的集合』と個人的に呼ぶことにします。
(キューネン本では、『(所属による)推移的集合』のことを、端的に『推移的集合』と呼んでいます。
あってしかるべきはずの、ただの推移的集合の呼び方については、特に何も書いてありません。)
1_2_1_1_B(成果物の下準備1-B).(所属による)整礎的関係
整礎的関係においても、その順序が所属で成り立っているものを考えることができます。
これは、ある集まりが別の集まりに所属していて、いつか自分に戻ってくることがなく、どこかに伸びていくような、そんな集合たちの、ある種の整礎的関係です。
この場合、「aがbに所属して、bがcに所属して、cがaに所属するような集合たち」(ジャンケンの三すくみ関係が正にそうですね)や、「自分自身を所属させる集合」は、この中には存在しません。
この伸びた集合たちは、それぞれが一里塚であるような、ある種の順序関係を持ちます。つまりこれが「所属による」「整礎的関係」です。
***
ちなみに、上で述べた、伸びた集合たちは、前述の(所属による)推移的集合になってもいます。
***
後に、「全ての集合において」、巡回的な所属を持つ集合たちや、自分自身を含む集合を禁じるのに効果のある、あるZFC集合論の公理の1つ、『基礎公理』について、説明することになります。
が、だいぶ後の話です。
1_2_1_2(成果物の下準備2にして中間成果物1).(所属による)整列順序
さて、もし「整列順序」が、「(所属による)推移的集合」による、「(所属による)整礎的関係」でもあるならば、「所属による整列順序」を考えることができます。
整列順序はパターン化できますが、それのパターン化の基準に、この所属による整列順序が使われます。
さらに、この場合のパターン化は、「これらの整列順序と、所属による整列順序が、全単射で照らし合わせると完全に対応する」ことで成り立ちます。
ということで、ここで全単射が出てくるんですね。
実は、さっき言っていた「特別な整列順序」とは、「所属による整列順序」のことなのでした。
***
(整列順序を持たないが、(所属による)整礎的関係を持つ(所属による)推移的集合はどうなるのか、という話は当然ありえますが、これは後になってから扱います)
1_2_1_3(成果物).順序数
そして、所属による整列順序における整列可能集合は、最も原始的な「数」、すなわち「順番を数えられる」「数」と同じ機能があります。
ということで、こうして作られた「順番を数えられる数」を、『順序数』と呼びます。
これが順序数の一般的な定義です。
***
ひょっとして昔、なんかどこかで
「自然数には順序数(順番)の性質と基数(個数)の性質がある」
という話を聞いたかもしれません。
順序数とはこれのことです。
「では、基数とはどのようなものか?」
当然こういう話が出てくるのですが、後で説明します。
(先に申し上げますと、基数は順序数によって定義されるような、あるものです。)
1_2_1_4.順序数の具体的な構成
さて、本当にこの順序数が、我々の考える、「順番を数えられる数」ということで問題ないのか?
実際に順序数を作って、確かめてみなければなりません。
ということで、順序数の一般的な定義「はいったんさておいて」順序数の具体的な構成をします。
特に、順序数のうち、0と、後続順序数の話をします。
1_2_1_4_1.順序数0
空集合を順序数と見立てて、順序数0とします。
1_2_1_4_2.(和集合としての)後者函数
細かい話を言うと、順序数1を作る、後者函数としての最初のステップでは、実際には順序数の特殊な和集合を使っているのです。
そして、上記の形の順序数の特殊な和集合は、「この時点では」別に(広義の)函数でも何でもないのです。
『後者函数』という名前だけ見ると『(広義の)函数』に見えますが、実際に(広義の)函数を構築し、(広義の)函数として使うのは、もう少し後の話になります。
1_2_1_4_3.後続順序数1
さて、順序数0(空集合)に後者函数を適用すると、結果的に空集合を要素とする単元集合が得られます。
これが実は、「次の」順序数の具体例の1つ、順序数1です。
1_2_1_4_4.((広義の)函数としての)後者函数
順序数1に後者函数を適用すると順序数2が、順序数2に後者函数を適用すると順序数3が得られます。
ちなみにここで使っている『後者函数』は、上記の形の順序数の特殊な和集合と、加工された新たな順序数との、順序対で出来ていると見なせるので、よくよく調べるとつまりはそういう『(広義の)函数』であることが分かります。
後者函数における最初の順序対のそれぞれの要素、0と1が整ったら、そこからは後者函数は(広義の)函数として扱える。という訳です。
1_2_1_4_5.後続順序数2以上
こうした作法で得られた場合の、1および2以上の順序数(要するに1以上の順序数)を、後続順序数と呼びます。
(「もっと大きい、後者函数で作れない順序数」、『極限順序数』というものもあります。
今回の記事では基本的に説明しませんが、次回出てきます)
1_2_1_4_6.順序数として具体的に構成された順序数0及び後続順序数が順序数の一般的な定義を満たすこと
そして、順序数0及び後続順序数は、(所属による)推移的集合としての性質を満たします。
集合の要素は集合であり、そのまた要素は集合です。
(遡る方を考えると、空集合、0で、そこからはもう遡れない、行き止まりになります)
そしてこれは(所属による)整列順序でもあります。
順序数0及び後続順序数は、一直線上の構造を持ち、0も1も2も3も、全部一里塚として存在します。
つまり、順序数の一般的な定義で行なった説明が、順序数の具体的な構成においても、ちゃんと成立しているのですね。
1_2_2.順序数としての自然数
流派によりますが、後続順序数、あるいは0と後続順序数(キューネン本2冊ではこちらを採用しており、この記事でも同様とします)こそが、『順序数としての自然数』に他なりません。
まずこの時点で驚きます。こんな風に作るのだし、そして作れるのです。
そして、言われてみれば、「この」0や1や2や3は、確かに、我々の知る、0であり1であり2であり3です。
少なくとも、順序という意味では。
2.次回予告
次回は、「基数としての自然数」、『有限基数』または『個数』と呼ばれるものについての話をします。
これをしたら自然数そのものの話をしたのと同じ意味になります。
(続く)
いいなと思ったら応援しよう!

