
番外編:(世界一わかりやすい)斜交座標のすゝめ ~図形問題を考えずに解く~
高校受験で必ずと言っていいほどでる図形問題。「こんな補助線わかるか!」や「メネラウスの定理とか習ってない定理出すな!」とかいう悲痛の叫びが聞こえてきます。
「図形問題はもはや知識とセンスではないか?」「俺は関数のほうが得意だしぃ」と思うのはあるあるでしょう。
ではどうするか?
図形問題を座標にすればいい!
図形を座標にすると、ややこしい図形問題も関数の問題のようにとくことができます。これで、センスゲーの図形問題とはおさらばです。ということで、斜交座標編スタートです。
※この記事では「高校受験で使える斜交座標」に関する知識を一から百まで解説しています。つまり、この記事を読むだけで「高校受験で使える斜交座標」完璧に理解できます!ぜひ、鉛筆を片手にじっくり読んでみてください。
斜交座標とは?
ある程度図形問題をやったことがある人なら、図形を関数にしてもよいのではないかと思うでしょう。ですが問題なのは、直交座標(=中学校で扱う座標。X軸とY軸が直交する)では辺の関数が複雑なものになってしまうという点です。ここで、斜交座標を導入してみます。
斜交座標とは、普段の直交座標をつぶしたような・ゆがましたような形(X軸とY軸が斜めに交わる)で表す座標のことです。
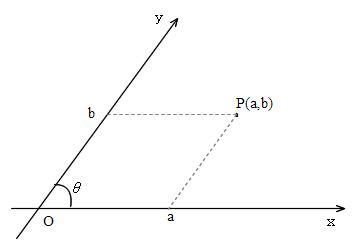
この座標を理解するには、ベクトル(高2範囲)を理解しないといけません。皆さんは中学生ですので、おおざっぱなベクトルの説明をしておきます。
ベクトルとは?
ベクトルとは、向きと長さを持った量のことです。矢印であらわします。
対して、4や6のような皆さんが知っている、長さしか持っていない量(数)つまり、ただの数のことをスカラーといいます。

ベクトルについての理解を深めてもらうために、例を挙げます。上の図で、青いベクトルは、x軸方向に1、y軸方向に4移動しているので、このベクトルは(1,4)と表します。同様に、赤いベクトルは(4,-6)と表します。この( 、)という表し方を成分表示といいます。
(x成分、y成分)です。
スカラー倍ベクトルの和とは?
ここで、ベクトルの和、スカラー倍について考えます。まずは例から…

青色のベクトルと赤色のベクトルを使って、緑色のベクトルと同じ量を表すことを考えます。
まず、青色のベクトルを一つ置き、その先から赤色のベクトルの半分を置くと、その先っぽは緑色のベクトルの先っぽと重なります。

つまり、、
青いベクトルを aベクトル
赤いベクトルを bベクトル
緑色のベクトルを cベクトル とすると、
緑色のベクトルは、 a + (1/2)b = c と表すことができます。
これを成分表示に直して計算してみると、
(1,4) + (1/2)(2,-2)=(1,4) + (1,-1)
=(2,3)
これは、緑のベクトル(cベクトル)の先っぽの位置(2,3)と一致します。
この計算には、この段落のテーマ、「ベクトルの和」と「スカラー倍」の両方が詰まっています。
まず、bに1/2をかけていることは「スカラー倍」にあたります。スカラーというのはただの数字(例1では1/2)のことでしたね。ベクトル自体を1/2倍するのだから、x成分とy成分のどっちともを1/2倍するのは当たり前ですよね。
これは相似の考え方といってもいいでしょう。
一般に
k(a,b) = (ka, kb) ※Kはスカラー
次にベクトルの和についての説明です。例1ではベクトル同士(aベクトルとbベクトルの半分)を足していますが、それを「ベクトルの和」といいます。ベクトルの和は「矢印で道を作って、その終着点を出発点としてもう一度矢印で道をつくる。一つ目の矢印の始発点と二つ目の矢印の終着点を結ぶ」という考え方です。例えると「回り道をしても、結局はこんだけしか進んでいないよ」ということです。
(a, b) + (c, d) = (a + c, b + d)
「スカラー倍」「ベクトルの和」この二つは感覚で理解しちゃってください!!
斜交座標とは?
さぁ、長い長い前置きが終わりまして、やっと斜交座標の話に入っていきます。
斜交座標は、ベクトルが何個つながっているかを軸の単位にとった座標です。んーわからないですよね。 例題に行きましょう。その前に、斜交座標の大切なことを示します。
斜交座標上で、
平行線分の長さの比
面積の比
は、どの座標系=座標の種類(直交座標,斜交座標etc…)でも変わらない。
どういうことか、そしてどう活用するのか?それをこれからの例題で解いてみましょう。
例題
次の問題を見てください。
注:文字がかなり小さくなってしまっています。紙に問題を移すなどして対応していただけると嬉しいです。

この問題、相似を使って解くと瞬殺ですが、今回はわざと斜交座標を使って解いてみましょう。
Step1: 座標にするために、座標のメモリを決める。
上の図のように、問題を回転させ、2つの一次独立なベクトルを作ります。今回は、座標のメモリが矢印です。次にこれをもとに座標に直します。

Step2:直交座標に変換する
ここで、考えやすいようにこの斜交座標を直交座標に変換(斜交座標の軸を縦と直す感じ)します。これをすることができるのは、先ほど示した「斜交座標の大切なこと」である、
斜交座標上で、
平行線分の長さの比
面積の比
は、どの座標系=座標の種類(直交座標,斜交座標etc…)でも変わらない
という性質があるからです。辺の比が、斜交座標上で1:3ならば直交座標上でも1:3を取る、ということです。
先ほどの斜交座標であらわした三角形を、直交座標に変換すると次のようになります。


これをすると、辺を関数で表すことができるということがわかるでしょう。具体的な関数も載せておきました。
Step3: 比を出す
BIの長さを求めたいので、
BI:IHを求めるところから始めましょう。
そのためには、Iの座標が知りたいですね?
Iの座標は、緑色の関数と、青色の関数の交点です。つまり、

で求められます。ここで、
x=1/3
と出ます。長さの比は、x座標の比になる(相似より)ので、
BI : IH = x : 3-x
= 1 : 8 になります。
Step4: 答えを出す
BI : IH = 1 : 8 と、相似でBH = 3DF ⇒ BH = 9
より、BI = 9 × 8/1+8 = 8とわかります。
よって、答えは
8!!!
正解です!!ヤッター。
応用例題
しかし、先ほどのようなシンプルな問題では斜交座標を使って解くと時間オーバーは必至です。
次の応用例として、斜交座標を使って解く時間を短くできる問題を解説します。
問題

上位校を受験する皆さんには、この手の問題はメネラウスの定理を使えば良いという思考が問題集や塾のおかげで刷り込まれていると思いますが、メネラウスの定理って、AかDかどっちで始めるのかがごっちゃになりません?
ということで、この問題を今回は斜交座標を使って解いてみましょう。
答え
この先 答えです。一回といてみてからこの先を見てください。
例題のように、基底のベクトル(直交座標に変換したときにX軸になるやつ=今回はAD)を決定します。今回は比を求めるだけでいいので、ABとADを単位ベクトル(長さを1と定めてほかの長さの基準にするベクトル)として斜交座標を書きます。そのあと、直交座標に変換(くどいですが、この作業は、、)。
斜交座標上で、
平行線分の長さの比
面積の比
は、どの座標系=座標の種類(直交座標,斜交座標etc…)でも変わらない。
この性質があるので、、、

となるのは、例題を理解した皆さんなら簡単でしょう。これからはもっと簡単な座標計算に移ります。
まず、求めたいのは緑と紫の関数の交点です。これらの関数は、

と表せます。これらを連立すると、
x=1/3
と出てきます。相似の考え方を使い、辺の比はx座標の比と考えると、
BO : OC = 1 : 2
です。
皆さん、あっていましたか?
まとめ
今回は、一般的に、高校生が2年から3年にかけて学ぶベクトル・斜交座標を用いて、高校受験の図形問題を簡単に解く方法について解説しました。比の問題をただの座標計算にできる点は非常に魅力的ですし、斜交座標を直交座標に直すという考え方はどんな図形問題にも応用できます。
しかし、中学生の皆さんにとっては非常に難解なものであったかもしれません。なので、理解しなくても良いです。というか、斜交座標を勉強するよりもオーソドックスな解き方を反復したほうがためにはなるかもしれません。
それでも、この記事を見て斜交座標の魅力をわかってくれた人は受験にとらわれずに数学を極めていってほしいし、それが受験の集大成である大学受験につながると思っています。数学の奥深さを感じてくれた人が一人でもいたら光栄です。
ご精読ありがとうございました!!
written by いますがり
ライター紹介
いますがり
地元の公立中学校からきた数学が好きな現役高校生。好きな数学の単元は関数。最近の趣味は関数グラフで遊ぶこと。
受験の朋(じゅけんのとも)
現役高校生が立ち上げた、高校受験を経験することで得た、上位高校に合格するために必要な情報(ノウハウ)を共有するためのウェブメディア。現在メンバーは5人(2024/7/4日現在)
ツイッター(じゅけともメンバーが思ったことを自由に投稿)
@jukennotomo
アメブロ(基本的にnoteと同内容)https://ameblo.jp/juketomo/entrylist.html
公式LINE(質問・リクエスト・連絡など)
https://lin.ee/mr7pFzy
受験の朋では一緒に活動してくれる高校生を募集しています。ぜひ気軽にご応募ください。
応募・詳細は下のリンクからお願いします。
