
算数授業のオープンエンドアプローチ 〜算数に価値観を入れる〜
算数が研究授業のテーマ教科
私の勤務する小学校では、各教師が自分の授業を同僚の教師に公開する「研究授業(校内研)」というものがあります。ほとんどの小学校では、そういった「研究授業」なるものが実施されていると思います。
研究授業には、小学校の教員として、
授業立案から当日の授業技術までを含んだ研修的な意味合いがあります。
研究授業の教科は、国語だったり、算数だったりと学校やその年度によっても変わりますが、算数で考えてみます。
算数教科書の特色
『道のり(解き方)は多様にある』
最近の算数の教科書は、
答えを「ゴール」とすれば、
『道のり(解き方)は多様にある』というスタイルを持っています。

上のページのかけ算の学習の一例では、
①あるものを数える
②枠全体の数を計算して、あいているとこ分を引く
という2つの解法(道のり)が登場しています。
解放は複数あるということとと、
それぞれの考え方を説明したり、違いを違いを見出したりと、
他者と考えを交流することも重視されています。
「すでに学んだことを活かして方程式を考える(自ら作り出す)」
また、方程式をただ紹介するのではなく、
「すでに学んだことを活かして方程式を考える(自ら作り出す)」ような内容だったりもします。そうすることで、方程式の意味を自分で理解するといことにつながるのだろうと思います。
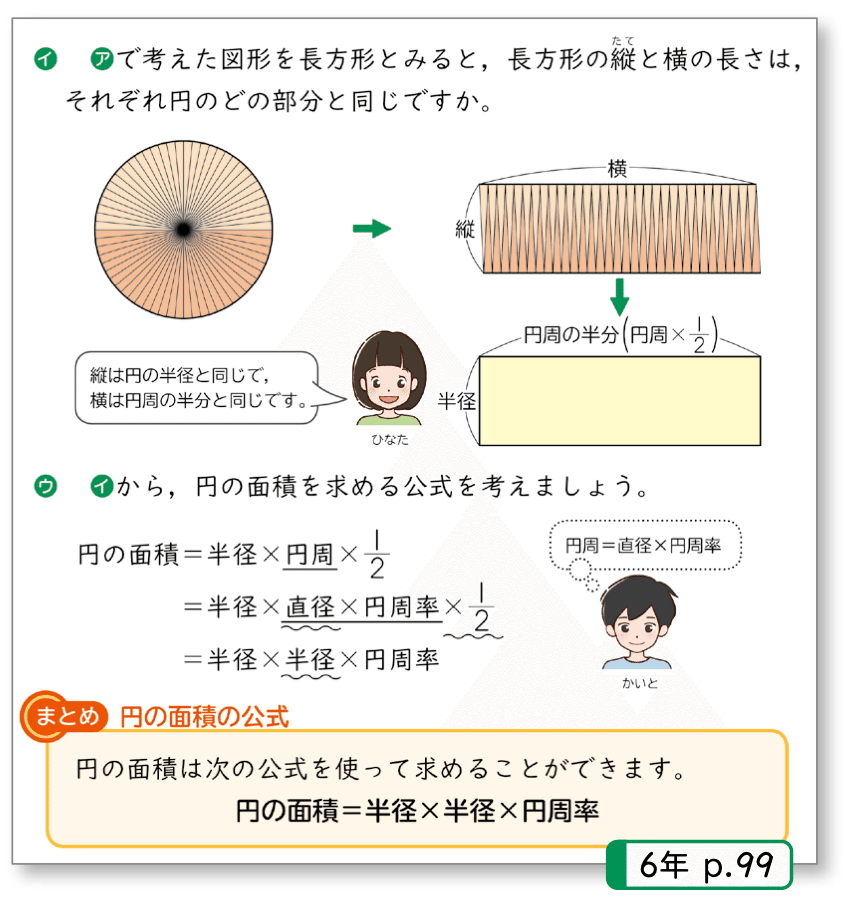
上の事例では、すでに習った内容「円周=直径✖️円周率」を参考に、
円の面積の方程式を考える内容となっています。(難しいですが)
上の2つのこと
「道のり(解き方)は多様にある」
「すでに学んだことを活かして方程式を考える(自ら作り出す)」
はとてもよい思考のトレーニングになると思います。
私は「算数のトレーニングで鍛えた思考」について、
できるだけ「実社会との繋がりを持ってもらいたい」
「それぞれの考えを生み出してほしい」と考えています。
算数授業のオープンエンドアプローチ
算数は、「答え」がはっきりとしている教科です。
その答えへのアプローチは多様な道のりがあるのは先述した通りですが、
算数では「答え」が複数あるということは取り扱いにくいのかもしれません。
しかし、「算数」を使った判断であるならば、
子どもたちが多様な意見を考えることができます。
算数の研究授業を考えるに当たり、
色々と調べた中で「これは自分が考えている方向性と同じだな」と思った算数の考え方があります。
それが、「算数授業のオープンエンドアプローチ」です。
「オープンエンドアプローチ」は、
答えが一つではなく、多様な意見がでるような学習内容であり、
そのような問題を「オープンエンドな問題」と言います。
それに社会性を取り入れたものを「社会的オープンエンドな問題」と言われています。
オープンエンドアプローチは、新しい概念ではなく島田茂さんの
1977年の著書にまとめられていたそうです。他にも、たくさんの研究があるみたいですがここでは、深いりしないでおきますね。
算数の授業を考えるあたり、下の本を参考にしてみました。
アート作品のように揺さぶりをかける問題 〜算数界の仮定「同じものとみなす」を再認識する〜

再び、書籍『多様な価値観や数学的な見方・考え方を磨く算数授業のオープンエンドアプローチ』より引用します。
21本の花を3本ずつ束にします。花束はいくつできますか。
7人がこの花束を見て、「私は、この花束がいいわ。」「僕は、こっちの花束がいいよ。」「私もこれがいいわ。」といっています。どうして、「これがいいわ」と話し合っているのでしょう。(島田、西村、2006)
この問題は、算数界でのアートみたいなものだなと思いました。
「算数界の仮定」を改めて再認識させるような作品です。
これは、子どもたちに出題というよりも、
教育に携わる大人たちへの出題だなとも感じました。
本当の花は、色も、形も違うはずです。
この問題を実際に取り扱った実証研究『仮定をおく力の育成を目指す授業に関する研究 ー算数と社会をつなげる力の育成を目指してー(島田攻、西村圭一2008)』では、以下の意見がでたそうです。
C1新鮮さが違うから
C2 色が違うから
C3茎の長さが違うから
C4種類が違うから
C5花の形が違うから
C6花の大きさが違うから
C7花のにおいが違うから
C8虫がついていたりするから
C9値段が違うから
C10長持ちする花としない花だから
C11つぼみがある花とつぼみがない花だから
https://www.jstage.jst.go.jp/article/jjsme/90/10/90_10/_pdf
実際の花には、上記のような要素がありどの花にもそれぞれの個性があります。
算数ではそれらの花を「同じものとみなす」仮定がある。
そんな、数学的本性を見つめ直す問題です。
リアリティー(花の個性)を考えさせておいて、
算数のスタンス(前提として同じものとみなせばよい)を認識した上で、
算数を行うという「前提を踏まえる」ことも大切だなと思いました。
一方で、私は「社会的価値観」により重点を置いた「社会的オープンエンドな問題」の方に関心が高いと感じました。
算数に価値観を入れる 〜6人家族、5個のケーキを分ける。〜
「社会的価値観」により重点を置いた「社会的オープンエンドな問題」
私の家族は、おじいさん、おばあさん、お父さん、お母さん、妹、私の6人家族です。ケーキを5個もらいました。このケーキをあなたは、どのように分けてあげますか。そう考えたわけも書きましょう。
設定は「6人家族、5個のケーキを分ける。」です。
6個ケーキを用意しておいてほしいところですが、
ケーキは5個、6人に1個づつ分けることができません。
小学校5年生の算数で扱う「分母の違う分数の計算」に関わる問題です。
ここで、多様な価値観が登場するとされます。
・完全に平等に分ける
・祖父母思い
・子ども優先
・大人優先
この問題から感じられることは「算数に感情を入れる」、
「算数に息吹を入れる」といいますか、
「算数に生活のリアリティーを入れる」といったことです。
このような実践は「算数」的な活動に100%振り切ったものではありません。
算数的な要素だけではない、
それぞれの「価値観」をもとに「判断」をする場面が重視されています。
なんかこのスタイルが好きですね。
判断するということは、そこに自分なりの「ストーリー」が生まれるからです。
そのストーリーが描けることが学びをより「リアル」になると感じます。
算数の「社会的オープンエンドな問題」の設定
先ほどのケーキを分ける問題がもし、「6人で、5個のケーキを分ける。」であれば、「スパッと平等に」となりやすかったかもしません。
しかし、その6人は『おじいさん、おばあさん、お父さん、お母さん、妹、私』でした。そうなったときに、この6人は匿名の6人ではなく属性を持つ一人一人の人間となり「判断」が多様に広がりました。
「判断が多様になる設定」とはどんな状況なのか?
・年齢の設定
「年下の子」:思いやりをもって、優先的に扱うこともあるでしょう。
「大人」体も大きく、たくさんの量を分配するという設定もあるでしょうし、
子供を優先させることもあるでしょう。
年齢は、小学校1〜6年生や、自分たちが体験してきた幼稚園親など身近な人もいたりするので、考えやすい要素ですね。
ちなみに、「令和4年度全国学力・学習状況調査の調査問題」の算数の中に、
年齢要素が関係している問題があります。

1年生の希望に重みをつけて、ポイント制にして「希望する遊び」の中からどの遊びにするかを判断している事例です。
・学校生活・行事的なものとの関わり
「1、6年生交流でする遊び内容の決め方」を6年生が決める
したい遊びのアンケートをとり、決定を行う。
年齢の設定で言えば、「1年生を優先的にする」という方向に集中しそうですね。
その他、みんなが楽しめる、安全であるなどの要素もありますね。
6年生の単元「データの調べ方」や「算数のしあげ」で取り扱う感じかな?
「6年生を送る会(卒業する6年生に向けて感謝の意味をこめて実施するイベント)を5年生が企画する
年齢の設定で言えば、
6年生を優先するか、低学年を優先するか。
先ほど同様、みんなが楽しめる、安全であるなどの要素もありますね。
やる内容のアンケートをもとに、
5年生算数単元「割合」、「帯グラフと円グラフ」などで取り扱う感じ。
保健室の統計データを利用して、改善策を一点検討する。
ケガをした場所、ケガの種類、ケガをした人数、時間、季節などを考慮に入れ、
ケガが多い原因と、その中でも一番減らしたいものを決める(大怪我を減らしたい、この季節のケガを減らしたい)。
減らしたいケガの原因に対して対策を考える。
6年生の単元「データの調べ方」や「算数のしあげ」、
5年生算数単元「割合」、「帯グラフと円グラフ」などで取り扱う感じ。
冬休み宿題の縄跳びカードの内容を分析し、練習メニューを考える
クラスでの練習の方向性を考える(個別練習もいれつつ)。
どの技が得意か、どの技があまり得意ではないか?
この技が得意だと→この技が得意、この技が苦手だと→この技も苦手
などのデータを分析したのちに、
重点課題を「判断」して、練習メニューを考える。
令和5年度 全国学力・学習状況調査 算数の問題ではこんなものがありました。

データから読み解いていく問題が続くのですが、
上のような「運動カード的なもの」ってよくあるなあと思い、
活用できるかもと思いました。
*個人の記録なので、個人情報の観点に留意しつつ
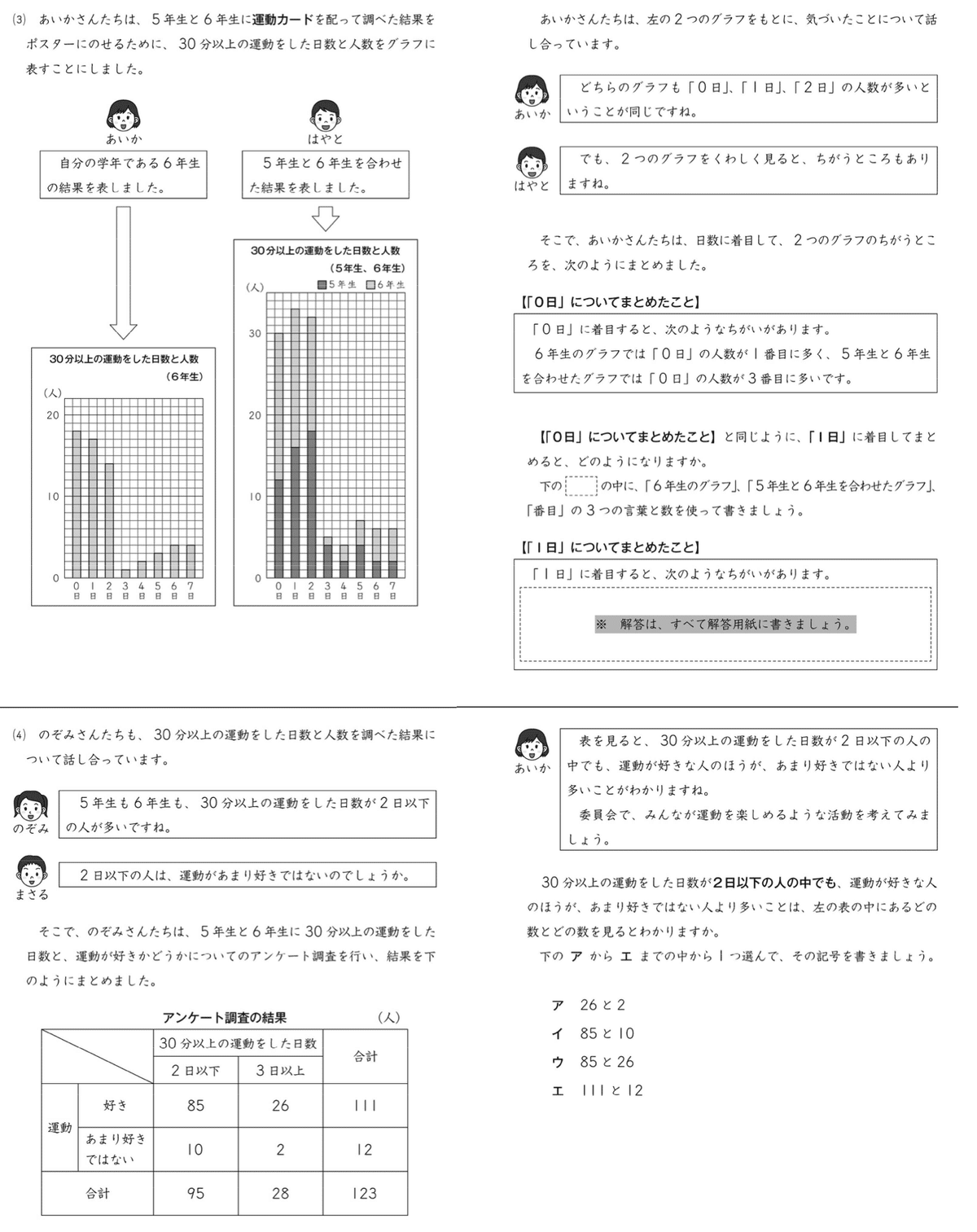
問題に登場する「あいか」さんのセリフには「委員会で、みんなが運動を楽しめるような活動を考えてみましょう」という文言が登場します。
『データをもとに、学校生活の中で判断して、実行する』ですね。
国立教育政策研究所さんの、令和5年度 全国学力・学習状況調査 報告書にある授業アイデア例では、データを読み取ってからさらに深掘りをしていく活動例が示されています。探究的ですね。
データを分析し、その結果から、さらに再調査を計画し、調査実施→分析→結論という流れです。

などなど。
授業の内容としては、算数で習得したものを使って「判断」する。
その「判断」も可能な範囲で実行できるものは実行できたらいいですね。
また、「判断」から再調査的な深掘りの流れも意識できらたいいなと思います。
算数の研究も奥深く、たくさんの方々によって、
長年の研究が積み重ねられています。
そこまで、深入はできていませんがそんな奥深さが「算数」にも、
「教育」にもありますね。
それでは、この辺で!
資料
国立教育政策研究所 教育課程研究センター「全国学力・学習状況調査」
https://www.nier.go.jp/kaihatsu/zenkokugakuryoku.html
*『仮定をおく力の育成を目指す授業に関する研究 ー算数と社会をつなげる力の育成を目指してー(島田攻、西村圭一2008)』では、
①隠れている仮定を見いだす授業
②隠れている仮定を見いだし、仮定を分類する整理する授業
③隠れている仮定を見いだし、仮定を置き換える授業
の実証授業を扱っていました。https://www.jstage.jst.go.jp/article/jjsme/90/10/90_10/_pdf
算数と社会をつなげる力に関する研究
https://www.jstage.jst.go.jp/article/jjsme/86/8/86_3/_pdf
