
世の中にある本をすべて読もうとすると何年かかる?(寿命は無視する)<上級編>ーー東大出身の理学博士が素朴で難しい問いを物理の言葉で語るエッセイ「ミクロコスモスより」⑤
前回の初・中級編では、
年間220万冊の本が出版されている現代の世界では、1日1万冊のペースで読めば、およそ100年で最新の本まですべてを読み切ることができる
という推測ができました。
「世の中にある本をすべて読もうとすると何年かかる?(寿命は無視する)<初・中級編>」はこちらから↓
しかし、この答えに違和感を持つ方もいらっしゃるかもしれません。
そのモヤモヤの正体とは……?
今回は上級編をお送りいたします。
∫∫∫∫∫∫∫∫∫∫∫∫∫∫∫
上級編
しかし、勘がいい人は、この答えだけでは納得しないでしょう。「人が本を読むペースは一生を通じて一定とは限らないのではないか」と気になる人もいるかもしれません。
すなわち、$${R}$$は定数ではなく、年齢$${Y-B}$$に依存する関数$${R(Y-B)}$$であるはず、ということです。
またある人は、「本の出版数は、あくまで近年では年間220万冊であるだけで、時代によって変化するのではないか」と言うかもしれません。すなわち、先に定義した関数$${P(Y)}$$はもう少し複雑な形をしているはず、というわけです。
人が本を読むペースは一生を通じて一定とは限らないのでは?
まず前者を考察してみましょう。人が自力で本を読むようになるのは、だいたい5歳前後です。そして、高校生から大学生にかけての時期に、もっとも読書量が増えるものの、その後は生活が忙しくなり読書量は減っていきます。また、年齢が上がり退職後は時間ができるため一時的に読書量が増えますが、視力の衰えとともにやはりペースは落ちていきます。これをモデル化してみましょう。

いきなりですが、こんな関数を考えてみます。

第一項は、幼少期から20歳にかけて読書量が増えていき、ピーク時には一日当たり$${R_0}$$冊に到達したのちに、また減少していく様子を表しています。
第二項は、社会人になり、一週間に1冊しか本を読めない様子を表しています。
第三項は、定年退職後に読書量が増え、その後に体力の衰えとともに減っていく様子を表しています(ピークの読書量も、若い頃よりは低いことを想定しています)。
指数関数に含まれるパラメータ$${a}$$は「余生の長さ」を表しています。

1日当たりの読書量Rの推移
※1 当然ながら、今回の考察のために場当たり的に考案したモデルであり、何も客観的な根拠はありません。このような「机上の空論」を根拠のある理論にするためには、現実のデータを充分再現できることを確かめる必要があります。
本の出版数は、あくまで近年では年間220万冊であるだけで、時代によって変化するのではないか?
次に、$${P(Y)}$$についても考察してみます。
一般に、紙の書籍はどんどん減っていると言われていますが、本そのものは電子媒体でも配信されるようになり、必ずしも減っているとは言い切れません。むしろ、より簡単に本を世に出すことができるようになり、1年あたりの出版数は今後増えることも考えられます※2。しかし、単純に1年あたりの出版数が増え続けると仮定してしまうと、何年かかっても読み切れない、という結論になってしまいます。
ここでは恣意的に、1年あたりの出版数がある値$${P_\infty}$$に漸近していく(「だんだん近づいていく」意味の数学用語)と仮定しましょう。
※2 例えば次のようなデータがあります。
「2021年紙+電子出版市場は1兆6742億円で3年連続プラス成長~出版科学研究所調べ」https://hon.jp/news/1.0/0/32230
すると、こんな形になります。

2010年時点では$${P(Y)}$$が1億3千万冊かつ$${\frac{d}{dY}P(Y)}$$が220万冊/年であったことから、
$$
P(2010)=P_\infty\left[1-\exp{\left(-\frac{2010}{b}\right)}\right]
$$
すなわち、
$$
P(Y)=130,000,000\times\frac{1-\exp{\left(-\frac{Y}{b}\right)}}{1-\exp{\left(-\frac{2010}{b}\right)}}
$$
と書くことができます。
また微分係数についても、
$$
\frac{d}{dY}P(Y) = 2,200,000\times\exp{\left(-\frac{Y-2010}{b}\right)}
$$
と表せます。
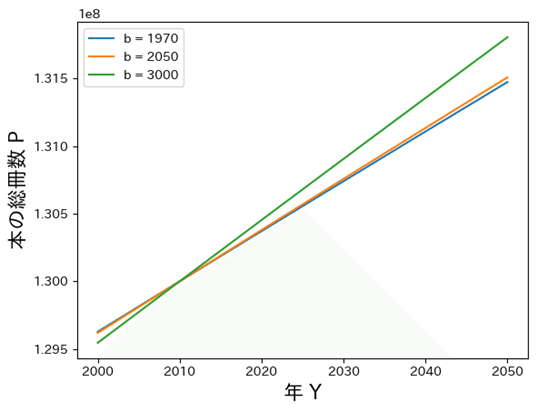
さて、準備が整ったところで問題を解いていきましょう。改めて、解くべきものは次の方程式です。
$$
\frac{d}{dY}Q(Y)=-R(Y-B)\times365.2425+\frac{d}{dY}P(Y)
$$
この$${Q(Y)}$$がゼロになるような$${Y}$$を求めれば、$${Y-B}$$が必要な寿命である、ということになります。
最大読書量$${R_0}$$、余生$${a}$$および本の出版数が飽和する年$${b}$$という、3つの自由パラメータ(正確に予測できない、またはモデルによって制約されることができない数学的モデル内の変数)があります。
ここでは深く考えずに、誕生年は$${B=1995}$$年、$${R_0=5}$$、$${b=2050}$$を仮定し、$${a}$$は充分長い年数を選ぶことにします※3。
※3 充分余生$${a}$$が長くなければ本を読み切れないということはあらかじめわかっているので、有限の時間で本が読み切れるような長大な余生を選ばなければ、解が存在しなくなってしまいます。
計算の結果がこちらのグラフです。

余生$${a}$$が500年くらい、すなわち寿命が560年程度だとすると、青の線のように未読冊数を減らせないまま寿命が尽きてしまいます。一方、寿命が13万年あれば、オレンジの線のように最新の本に追いつくことができます。
この結果は、最初に見積もった「7万年」という値に近いものです。
つまり、2000年前後の時点では、それまでに出版された本があまりにも多いため、もはや今後新しく出版される本の影響は小さいということが分かりました。
ゲーテの戯曲「ファウスト」では、悪魔との契約で散々な目に遭った結果、社会や人のために生きることに喜びを見出すことになります。たとえ悪魔と契約して10万年以上の寿命を得てすべての本を読み切ったとしても、きっとファウストのように知識欲が消えることはないでしょう。
プロフィール
小澤直也(おざわ・なおや)
1995年生まれ。博士(理学)。
東京大学理学部物理学科卒業、東京大学大学院理学系研究科物理学専攻博士課程修了。
現在も、とある研究室で研究を続ける。
7歳よりピアノを習い始め、現在も趣味として継続中。主にクラシック(古典派)や現代曲に興味があり、最近は作曲にも取り組む。
この記事が気に入ったらサポートをしてみませんか?
