実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で②階層ベイズモデル

2024年2月7日 11:49

「PythonのMCMCライブラリPyMC」章

テキスト「PythonのMCMCライブラリPyMC」の執筆者
渡辺祥則先生

この記事は、テキストの「PythonのMCMCライブラリ PyMC」章の例題２「階層ベイズモデル」の実践を取り扱います。
この例題は久保拓弥先生の「データ解析のための統計モデリング入門」（通称、緑本）第10章の生存種子数データを利用しています。
そこで、緑本との整合も意識してモデリングに取り組みました。

はじめに

岩波データサイエンスVol.1の紹介

この記事は書籍「岩波データサイエンス vol.1」（岩波書店、以下「テキスト」と呼びます）の特集記事「ベイズ推論とMCMCのフリーソフト」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

テキストは、2015年10月に発売され、ベイズモデリングの様々なソフトウェアを用いたモデリング事例を多数掲載し、ベイズモデリングの楽しさを紹介する素晴らしい書籍です。
入門的なモデルから2次階差を取り扱う空間モデルまで、幅広い難易度のモデルを満喫できます！

このシリーズは、テキストのベイズモデルをPyMC Ver.5に書き換えて実践します。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「岩波データサイエンス vol.1」
第９刷、編者岩波データサイエンス刊行委員会　岩波書店

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

PyMC環境の準備

Anacondaを用いる環境構築とGoogle ColaboratoryでPyMCを動かす方法について、次の記事にまとめています。
「PyMCを動かすまでの準備」章をご覧ください。

PythonとPyMCの最新化
テキストのPyMCのバージョンはVer.3です。
また、テキスト発行の2015年から現在2024年までの約10年で、Python及び各種パッケージの利用方法が変わっています。
そこでこの記事では、テキスト掲載のPython＆PyMC3コードを自己流Python＆PyMC5コードに変換することを、実践事項の１つに取り上げようと思います。

例題２階層ベイズモデル

1. 前説

久保先生の緑本を参照して、観測データの概要を次のようにまとめました。

ある植物の$${100}$$個体について、各個体から$${8}$$個の種子を採取して、その中の生存種子数$${y_i}$$（$${0 \leq y_i \leq 8}$$）を調査しました。
観測データは「個体ID$${i}$$とその個体の生存種子数$${y_i}$$」にまとめられており、列は「個体ID：id」と「生存種子数：y」、データ形状は$${100}$$行、$${2}$$列です。

調査種子数$${8}$$、生存種子数$${y}$$、生存確率$${q}$$が頭をよぎりますね・・・
試行回数$${n=8}$$、成功回数$${y}$$、成功確率$${p=q}$$の二項分布を使いたくなります。

$$
y \sim \text{Binomial}\ (8,\ p)
$$

しかし観測データを概観すると「単純に二項分布を当てはめられない」ことが分かります。

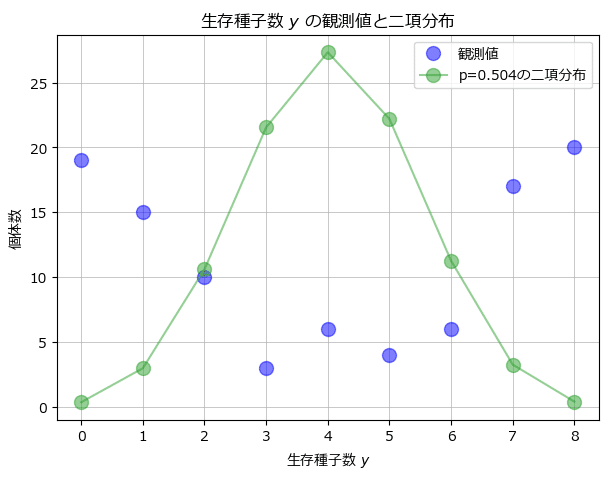
緑本の図10.1(B)をお借りしました。
青点の観測データは緑の二項分布と真逆の分布に見えます！
緑色の二項分布は全100個体で共通の生存確率$${q}$$（最尤推定値）で描いています。
つまり、全個体共通の生存確率パラメータでは、観測値を説明できないだろう、ということです。

そこで、階層ベイズモデルの登場です。
生存確率パラメータ$${q}$$に関して、「全個体共通のパラメータ$${\beta}$$」と「各個体ごとのパラメータ$${r_i}$$」に分けて推論し、さらに、個体ごとのパラメータ$${r_i}$$を推論するための事前分布を階層的に用意します。

前説はここまで。
PythonとPyMCのコードに進みましょう！！！

2. 準備

「PythonのMCMCライブラリPyMC」章で利用するパッケージをインポートします。

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 回帰分析
import scipy.stats as stats
import statsmodels.formula.api as smf
from sklearn.linear_model import LinearRegression

# 分類タスク
from sklearn.metrics import classification_report

# WEBアクセス
import requests

# yfinance株価データ取得
from pandas_datareader import data as pdr
import yfinance as yf

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

3. データの読み込み

久保先生のWebサイトからCSVファイルをダウンロードして、pandasのデータフレームに読み込みます。
テキスト掲載のURLから変わっていますのでご注意ください。
まずは、ダウンロードしてPCに保存します。
「# CSVファイルの格納フォルダ＋ファイル名」の箇所で、適宜、フォルダ名とファイル名を指定してください。

### CSVファイルのダウンロード

## 初期値設定
# ダウンロード元のURL
url = r'https://kuboweb.github.io/-kubo/stat/iwanamibook/fig/hbm/data7a.csv'
# CSVファイルの格納フォルダ＋ファイル名
path = './data/data7a.csv'

## ダウンロード
# Web接続
res = requests.get(url)
# ダウンロードファイルの保存
with open(path, mode='wb') as f:
    f.write(res.content)

続いて、データの読み込みです。

### データの読み込み
data2 = pd.read_csv(path)
display(data2)

【実行結果】
100行・2列です。
idは植物の個体ID。100個あります。
yは生存種子数です。調査対象の８個のうち生存した数です。
例えば１行目のID １番の生存種子数は０個です。調査種子数８個の全てが死滅したということです。

4. データの外観の確認

生存種子数ごとに個体数をカウントします。
テキストの図4に相当します。

### 度数分布表の作成とヒストグラムの描画
# ※図4に相当（テキストはID値の集計を表示しているが、この図は度数を表示した）

# 度数分布表の作成 pandasのvalue_countsで度数カウント
y_counts = data2['y'].value_counts().sort_index().to_frame()
display(y_counts.T)

# ヒストグラムの描画 実態は棒グラフです
plt.bar(y_counts.index, y_counts['count'])
plt.yticks(range(0, 21, 2))
plt.xlabel('生存種子数 $y$')
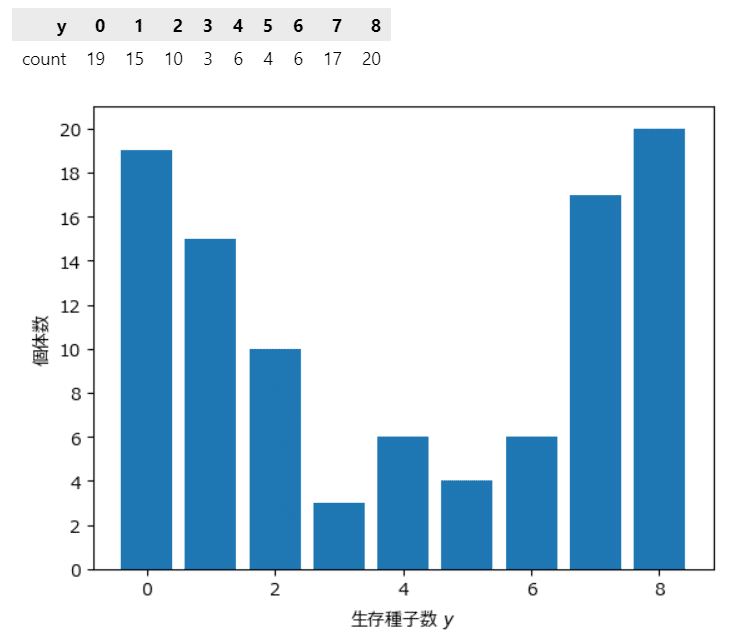
plt.ylabel('個体数');

【実行結果】
冒頭のグラフで見たとおり、凹型の形状です。
生存種子数は０個（全滅）と８個（全部生存）が多く、中央の４個付近の個数が少ないです。

緑本10.1節の種子生存確率の最尤推定と分散を計算してみましょう。
最尤推定には scipy.stats の fit 関数を利用します。
dist 引数に二項分布（stats.binom）、data 引数に読み込んだデータフレームの生存種子数（data2['y']）、bounds 引数に試行回数パラメータと成功確率パラメータの探索範囲（試行回数は０～８、成功確率は０～１）を指定しています。

### 生存確率qの最尤推定
# 最尤推定の実行
est_likelihood = stats.fit(dist=stats.binom, data=data2['y'].values,
                           bounds=[(0, 8), (0, 1)])
# pの最尤推定値の取得
p_est = est_likelihood.params.p
# 最尤推定結果の表示
print(est_likelihood)

【実行結果】
最尤推定値の算出は success しました！

試行回数パラメータ$${n}$$が$${8}$$のときに、成功確率パラメータ$${p}$$は$${0.504}$$。テキストと同じ結果になりました。

この成功確率パラメータ＝種子生存確率パラメータ＝$${0.504}$$と試行回数＝調査種子数$${8}$$を用いて、二項分布の分散を計算します。
二項分布の計算には scipy.stats の binom.var() を利用します。
観測データ y の分散は pandas の var() で計算しましょう。

### 分散の算出
est_var = stats.binom.var(n=8, p=p_est)
data_var = data2['y'].var()
print(f'n=8, p={p_est:.3f}の二項分布の分散 : {est_var:.2f}')
print(f'観測データの分散             : {data_var:.2f}')

【実行結果】
テキストと同じ結果です。
生存種子数の観測データはテキストのとおり「過分散」です。

ここで、冒頭の散布図の描画コードを確認しましょう。
二項分布のパラメータは$${n=8,\ p=0.504}$$です。
scipy.stats の binom.pmf() で二項分布の確率質量関数を計算しています。

### 観測値と最尤推定値を用いた二項分布の描画 
# 緑本10章 図10.1(B)に相当

## データ作成
# x軸の値
xticks = range(9)
# 最尤推定値を用いた二項分布の確率質量関数
binom_likelihood = stats.binom.pmf(k=range(9), n=8, p=p_est) * 100

## 描画
# 描画領域の設定
plt.figure(figsize=(7, 5))
ax = plt.subplot()
# 観測値の描画
ax.plot(xticks, y_counts, 'o', ms=10, color='blue', alpha=0.5, label='観測値')
# 二項分布の確率質量関数の描画
ax.plot(xticks, binom_likelihood, '-o', ms=10, color='tab:green', alpha=0.5,
        label=f'p={p_est:.3f}の二項分布')
# 修飾
ax.set(xlabel='生存種子数 $y$', ylabel='個体数',
       title='生存種子数 $y$ の観測値と二項分布')
ax.legend()
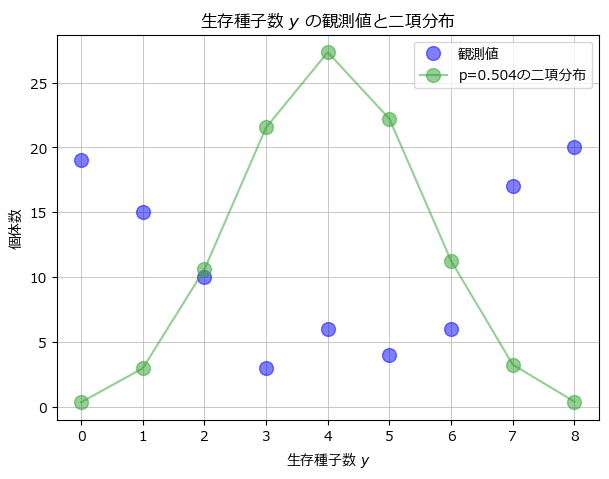
ax.grid(lw=0.5);

【実行結果】
冒頭の前説に追いつきました。

階層ベイズモデルに進みます。

階層ベイズモデル

1. 前説

■ モデル数式
テキストのPyMCモデルから数式を逆引きいたします。
事前分布から尤度関数の順で書きます。
なお、テキストのモデルは緑本と相違する部分があります。

$$
\begin{align*}
s &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\beta &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100) \\
r &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=s,\ \text{dims}=data) \\
q &= \text{invlogit}\ (\beta + r),\ \text{dims}=data \\
y &\sim \text{Binomial}\ (\text{n}=8,\ \text{p}=q,\ \text{dims}=data) \\
\end{align*}
$$

$${r}$$は個体差です。植物の個体IDごとに異なる性質を表します。
平均$${0}$$、標準偏差$${s}$$の正規分布に従うと仮定しています。
標準偏差$${s}$$は範囲の広い一様分布に従うと仮定しています。
$${r}$$と$${s}$$で二段構えの分布です。

$${\beta}$$は全個体共通のパラメータです。
平均$${0}$$、標準偏差$${100}$$の正規分布に従うと仮定しています。

$${r}$$と$${\beta}$$は正規分布で「縛り」をかけています。
$${s}$$は範囲の広い一様分布で縛りをかけない「無情報事前分布」としています。

種子生存確率$${q}$$は、回帰式$${\beta+r}$$を逆ロジット関数で確率値に変換した値です。
$${\beta+r}$$は線形予測子と呼ばれたりもします。
$${\beta}$$が全体切片、$${r}$$が個体別（群別）切片と捉えると、ランダム切片モデルかもしれません。
逆ロジット関数はロジスティック関数とかシグモイド関数とか呼ばれる関数です。

観測値である生存種子数$${y}$$は試行回数（調査種子数）$${n=8}$$、成功確率（種子生存確率）$${p=q}$$の二項分布に従います。
この部分は尤度関数と呼ばれたりもします。

標準偏差$${s}$$から尤度関数$${y}$$まで階層的に確率分布がつらなるこの形が階層モデルです。

注目するパラメータは個体差の標準偏差$${\boldsymbol{s}}$$と全固体共通の$${\boldsymbol{\beta}}$$です。

2. モデルの定義

数式モデルどおり実直にPyMCのモデルを定義しましょう。
なお、テキストは観測データの利用数を６個に制限していますが、このモデルでは制限せず、１００個全部使います。

### モデルの定義 　★データを6件に絞らず、全件利用しています

## データの定義
N = 8  # 調査種子数

## モデルの定義
with pm.Model() as model2:
    
    ### データ関連定義
    ## coordの定義
    # 観測データのインデックス
    model2.add_coord('data', values=data2.index, mutable=True)
    
    ## dataの定義
    # 観測値Y :種子数
    Y = pm.ConstantData('Y', value=data2['y'].values, dims='data')

    ### 事前分布
    # 個体ごとの要因 r
    s = pm.Uniform('s', lower=0, upper=100)
    r = pm.Normal('r', mu=0, sigma=s, dims='data')
    # 個体間共通の要因 β
    beta = pm.Normal('beta', mu=0, sigma=100)
    # 成功確率 q  ★invlogit関数はpymcに実装されました
    q = pm.Deterministic('q', pm.invlogit(beta + r), dims='data')
    
    ### 尤度:二項分布　種子数は最大8、個体ごとの成功確率qで種子数が決まる
    y = pm.Binomial('y', n=N, p=q, observed=Y, dims='data')

モデルの内容を表示・可視化してみましょう。
モデル名 model2 とタイプするとモデルの数式の概要が表示されます。

### モデルの表示
model2

【実行結果】

続いてモデルを可視化します。
１行のコードでグラフ形式の可視化ツール「Graphviz」に自動連携して、変数の関係を図示してくれます！

### モデルの可視化
pm.model_to_graphviz(model2)

【実行結果】
データやパラメータの繋がりが示されます。
丸い形状の変数には「確率分布」が併記されます。
$${s}$$、$${r}$$・$${beta}$$、$${y}$$へと確率分布の階層が形成されています。
データ値を示す変数はグレー色が付いています。

3. MCMCの実行と収束の確認

■ MCMC
いよいよベイズプログラミングの真骨頂 MCMC の実行です。
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを１chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。

サンプリングデータは idata2 に格納されます。

サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。

### 事後分布からのサンプリング 10秒
with model2:
    idata2 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=1234,
                       nuts_sampler='numpyro', target_accept=0.8)

【実行結果】
処理時間は約10秒です。

■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$（あーるはっと）の値が$${1.1}$$以下のとき、収束したこととします。
次のコードではしきい値を$${1.01}$$にキツく設定して、$${\hat{R}>1.01}$$のパラメータの個数をカウントします。
個数が０ならば、$${\hat{R} \leq1.01}$$なので収束したとみなします。

### r_hat>1.1の確認
# 設定
idata_in = idata2        # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R}>1.01}$$のパラメータは０個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示

### 事後統計量の表示
var_names = ['beta', 's', 'r', 'q']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names)

【実行結果】
MCMCでサンプリングデータを生成したすべてのパラメータについて、統計量や診断情報が一覧表示されました。

右端の$${\hat{R}}$$（r_hat）はすべて$${1.0}$$です。
上２行が注目するパラメータ$${\beta,\ s}$$です。
$${\beta}$$の推論値は、平均$${0.058}$$、95%HDI区間$${[-0.544, 0.736]}$$です。
$${s}$$の推論値は、平均$${3.032}$$、95%HDI区間$${[2.350, 3.813]}$$です。

■ トレースプロットで収束確認
トレースプロットを描画します。
テキストの図5に該当します。
こちらの図でも収束の確認を行えます。

### トレースプロットの描画 ※図5に相当
pm.plot_trace(idata2, compact=True, var_names=var_names)
plt.tight_layout();

【実行結果】
左の曲線は、４本のマルコフ連鎖の分布です。
４本の曲線がほぼ同じ分布を描いているので、サンプリングデータが同一の分布から生成されたことが推察できます。
右のノイズみたいな図は、均等に乱雑に描画されています。
この状態は収束していると推察できます。
均等・乱雑ではなくて、何らかの傾向を示すような描画の場合は収束を疑います。

$${\hat{R}}$$とトレースプロットから、分布の収束が確認できましたので、MCMCのサンプリングデータを用いて、推論を継続できます！
やったね！
事前分布に正規分布で一定の縛り（何らかの事前情報の投入）をかけたのが効いているのかもです。

■ 事後予測プロットでモデルの良し悪しを確認
もうひとつのプロットで推論の良し悪しを確認してみましょう。
目的変数$${y}$$の事後予測サンプリングを行ってグラフで可視化します。
事後分布からのサンプリング（MCMCのこと）では事後分布を得て「パラメータ」を推論します。
事後予測では、得られた事後分布を元にして「目的変数」を予測しちゃおうってことなのです！

### 事後予測サンプリングの実行
with model2:
    idata2.extend(pm.sample_posterior_predictive(idata2, random_seed=1234))

【実行結果】
中途半端な止まり方ですが、100個体数 × 4000個の事後予測サンプリングデータが作られました。

4000個のサンプリングデータのうち100個をランダムに選んで描画します。

### 事後予測プロットの描画
pm.plot_ppc(idata2, num_pp_samples=100, random_seed=1234);

【実行結果】
若干ズレていますでしょうか・・・

黒線が目的変数$${Y}$$の観測値、オレンジの点線が目的変数の事後予測の平均値です。
平均値は小数もありなので、整数値の観測値とズレているのかもしれません。

■ 予測精度の評価指数の確認
機械学習の評価指標を用いて、観測値と予測値の一致度合いを確認してみましょう。
平均値の小数を四捨五入で丸めて整数値に変換した上で精度確認します。
分類タスクの評価指標の計算・表示には scikit-learn の classification_report() を利用します。

### 予測精度の表示
## データの準備
# 正解値
y_true2 = data2['y'].values
# 事後予測値：事後予測サンプリングデータの平均値を四捨五入で整数に丸め
y_pred2 = (idata2.posterior_predictive.y.stack(sample=('chain', 'draw'))
           .mean(axis=1).data.round(0))
## 分類の評価指標レポートの表示
print(classification_report(y_true=y_true2, y_pred=y_pred2))

【実行結果】
オール１。つまり、予測値は観測値に完全一致しています！
過学習です！

まとめますと、今回のベイズモデルは目的変数をそこそこ表現できていると思います！
個体差$${r_i}$$を含む階層ベイズ、すごいですね！

4. 分析

■ パラメータの推論値の確認
パラメータ$${\beta}$$と$${s}$$を再度確認します。

### betaとsの事後統計量の表示と可視化
# 事後統計量の表示
var_names=['beta', 's']
display(pm.summary(idata2, var_names=var_names, hdi_prob=0.95, kind='stats'))
# 事後分布プロットの描画
pm.plot_posterior(idata2, var_names=var_names, hdi_prob=0.95, round_to=3,
                  figsize=(5, 3))
plt.tight_layout()
plt.show()
# フォレストプロットの描画
pm.plot_forest(idata2, combined=True, var_names=var_names, hdi_prob=0.95,
               figsize=(5, 3))
plt.axvline(0, color='red', ls='--')
plt.show()

【実行結果】

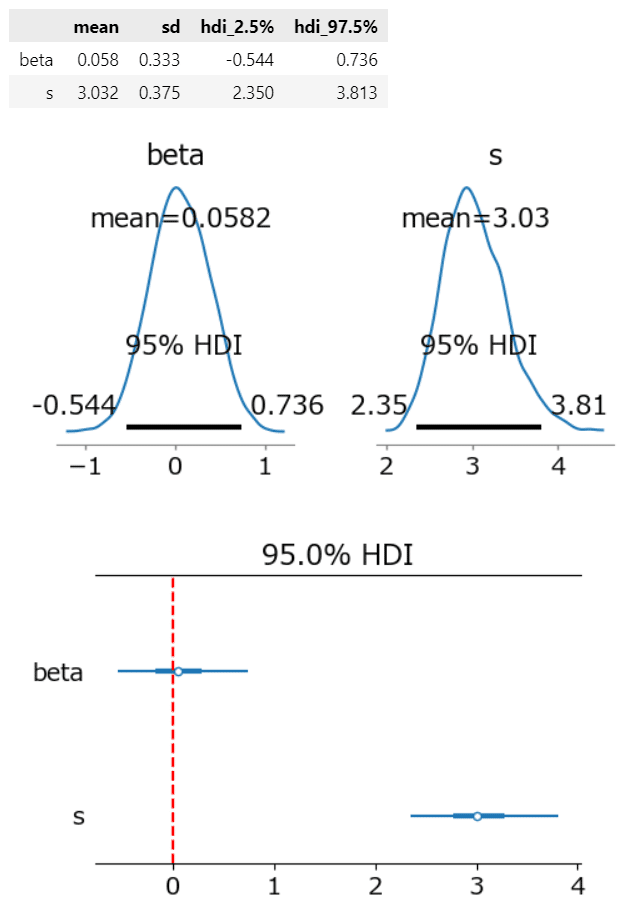
２つのパラメータの形状は正規分布のベル型に似ています。
$${\beta}$$は回帰式の切片に該当します。平均値はほぼ０。
この値はモデルにどんな影響を与えているのでしょう？？？
$${s}$$は個体差$${r}$$の従う正規分布のばらつきです。平均値は約３。

■ 生存種子数の予測、観測値との比較
２つのパラメータのMCMCサンプリングデータ各4000個を使って、生存種子数ごとの個体数を推論いたします。
緑本の図10.4「生存種子数$${y}$$の予測分布と観測データ」のグラフを描画します。

### 生存種子数の予測分布と観測値のプロット ※緑本10章 図10.4に相当

### 生存種子数の予測分布と観測値のプロット ※緑本10章 図10.4に相当

### 定義
# 乱数生成器の定義
rng = np.random.default_rng(seed=1234)

# 逆ロジット関数の定義
def invlogit_func(x):
    return 1 / (1 + np.exp(-x))

# betaとsから100個体の生存種子数乱数を生成、生存種子数ごとの個体数を返す関数の定義
def seeds_sampler(beta, s, N=8, size=100):
    # sを用いてrの正規分布乱数を100個生成
    r = rng.normal(loc=0, scale=s, size=size)
    # betaとRを用いて逆ロジット関数を適用し、確率qを100個作成
    q = invlogit_func(beta + r)
    # Nとqを用いて二項分布乱数＝生存種子数yを100個体分生成
    y = rng.binomial(n=N, p=q)
    # 生存種子数yごとの個体数をカウント
    num_index, counts = np.unique(y, return_counts=True)
    # 生存種子数0～8の個体数を整える（生存種子数0個を付加する）
    seeds = np.zeros(N+1)
    for i in range(len(num_index)):
        seeds[num_index[i]] = counts[i]
    return seeds

### 生存種子数の予測分布サンプリングデータの生成
## betaとsの事後分布からのサンプリングデータを取り出し
beta_samples = idata2.posterior.beta.data.flatten()
s_samples = idata2.posterior.s.data.flatten()
## 生存種子数y vs 個体数の予測分布サンプリングデータの生成、seeds_listに格納
seeds_list = []
for (beta_, s_) in zip(beta_samples, s_samples):
    seeds_list.append(seeds_sampler(beta_, s_))

### 描画
## データ準備
xticks = range(N+1)                   # x軸の値
seeds_samples = np.array(seeds_list)  # seeds_listをnumpy配列に変換

## 描画
# 描画領域の設定
plt.figure(figsize=(7, 5))
ax = plt.subplot()
# 観測値の描画
ax.plot(xticks, y_counts, 'o', ms=10, color='blue', alpha=0.5, label='観測値')
# 予測値（中央値）の描画
ax.plot(xticks, np.median(seeds_samples, axis=0), '-o', ms=10, color='red',
        alpha=0.5, label='予測値:中央値')
# 予測値（50%HDI区間）の描画
az.plot_hdi(xticks, seeds_samples, hdi_prob=0.50, color='tomato',
            fill_kwargs={'alpha': 0.5, 'label': '50%HDI'}, ax=ax)
# 予測値（95%HDI区間）の描画
az.plot_hdi(xticks, seeds_samples, hdi_prob=0.95, color='tomato',
            fill_kwargs={'alpha': 0.2, 'label': '95%HDI'}, ax=ax)
# 修飾
ax.set(xlabel='生存種子数 $y$', ylabel='個体数',
       title='生存種子数 $y$ の予測分布と観測値')
ax.legend()
ax.grid(lw=0.5);

【実行結果】
青い丸が観測値、赤い丸が生存種子数ごとの個体数の予測値の中央値、ピンクの濃い塗りつぶしが予測値の50%HDI、薄い塗りつぶしが予測値の95%HDIです。

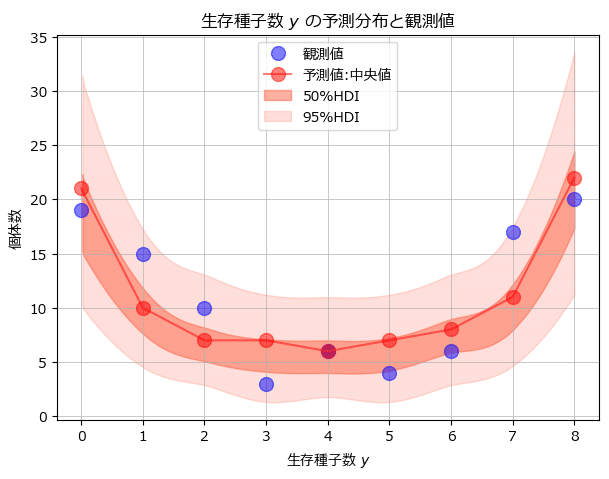
95%HDIは観測値が95%の確率で含まれる範囲であり、95%HDIにすべての観測値が含まれていますので、この階層ベイズはよく推論できているのではないでしょうか。
予測値（中央値）と観測値を比べると、観測値の凸凹の真ん中辺りを塗って予測値がプロットされています。
予測値は観測値のばらつきをやわらかに緩和している感じがいたします。

ベイズモデルのいいところの１つは、MCMCによるパラメータの事後分布サンプリングデータを活用して、確率的な分析を容易にできることです！

【参考】 seeds_sampler 関数による予測値シミュレーション

このコードでは、中段あたりの関数「seeds_sampler」が、$${\beta,\ s}$$のペアごとに生存種子数$${y}$$の乱数を１００個（つまり個体数１００個）作成して、生存種子数単位で個体数をカウントする、といった予測計算を担っています。
PyMCモデルの推論と同じ確率分布や計算を行っているのです。

実験してみましょう。
$${\beta}$$と$${s}$$に値を設定して関数「seeds_sampler」を動かします。

### 関数の動きの確認
seeds_sampler(beta=0.455, s=2.9)

【実行結果】

左から、生存種子数が０、１、・・・、７、８個に対応する「個体数」です。
生存種子数０個の個体数は１８，生存種子数８個の個体数は２０個です。
上記コードではこの予測値データを4000個分作成して、中央値やHDIの計算に利用しています。

ね。
MCMCによるパラメータの事後分布サンプリングデータって、いろんな活用ができますね！

5. 推論データの保存

pickle で MCMCサンプリングデータ idata2 を保存できます。

### 推論データの保存
file = r'idata2_ch1.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata2, f)

次のコードで保存したファイルを読み込みできます。

### 推論データの読み込み
file = r'idata2_ch1.pkl'
with open(file, 'rb') as f:
    idata2_ch2_load = pickle.load(f)

ベイズ記事は以上です。

次回予告

「PythonのMCMCライブラリ PyMC」章
　例題３「離散変数のサンプリング」

結び

緑本を久しぶりに開きました。
今までは一般線形モデル（GLM）も一般線形混合モデル（GLMM）もベイズモデルも良く理解できないまま、世の中にはいろんな統計モデルがあるんだなぁ、といわば引き気味に見てきました。

最近、ベイズプログラミングを学ぶ中で、GLM、GLMMなどが当たり前のように用いられ、知らず知らずのうちに、GLM、GLMMのモデリングに接してきました。
そのおかげで、今回、緑本を見返したときに、気づきや納得感などの体感（アハ体験みたいなもの）を得ることができました。
もう一度、きちんと学び返そうと、心新たにしました。

おわり

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

いいなと思ったら応援しよう！

この記事が参加している募集

#お金について考える

42,355件

実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で②階層ベイズモデル

「PythonのMCMCライブラリPyMC」章

はじめに

岩波データサイエンスVol.1の紹介

引用表記

PyMC環境の準備

例題２ 階層ベイズモデル

1. 前説

2. 準備

3. データの読み込み

4. データの外観の確認

階層ベイズモデル

1. 前説

2. モデルの定義

3. MCMCの実行と収束の確認

4. 分析

5. 推論データの保存

次回予告

結び

シリーズの記事

ブログの紹介

いいなと思ったら応援しよう！

この記事が参加している募集

例題２階層ベイズモデル