StanとRでベイズ統計モデリングをPyMC Ver.5で写経～第11章「11.3 ゼロ過剰ポアソン分布」

2024年4月6日 10:23

第11章「離散値をとるパラメータを使う」

書籍の著者　松浦健太郎先生

この記事は、テキスト第11章「離散値をとるパラメータを使う」の 11.3節「ゼロ過剰ポアソン分布」の PyMC5写経 を取り扱います。
PyMCのゼロ過剰ポアソン分布クラス ZeroInflatedPoisson() を用います。

はじめに

StanとRでベイズ統計モデリングの紹介

この記事は書籍「StanとRでベイズ統計モデリング」（共立出版、「テキスト」と呼びます）のベイズモデルを用いて、PyMC Ver.5で「実験的」に写経する翻訳的ドキュメンタリーです。

テキストは、2016年10月に発売され、ベイズモデリングのモデル式とプログラミングに関する丁寧な解説とモデリングの改善ポイントを網羅するチュートリアル「実践解説書」です。もちろん素晴らしいです！
「アヒル本」の愛称で多くのベイジアンに愛されてきた書籍です！

テキストに従ってStanとRで実践する予定でしたが、RのStan環境を整えることができませんでした（泣）
そこでこのシリーズは、テキストのベイズモデルをPyMC Ver.5に書き換えて実践します。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「StanとRでベイズ統計モデリング」初版第13刷、著者松浦健太郎、共立出版

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

PyMC環境の準備

Anacondaを用いる環境構築とGoogle ColaboratoryでPyMCを動かす方法について、次の記事にまとめています。
「PyMCを動かすまでの準備」章をご覧ください。

11.3 ゼロ過剰ポアソン分布

インポート

### インポート

# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 線形回帰分析
import statsmodels.formula.api as smf

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# 共分散楕円の描画
# !pip install filterpy
from filterpy.stats import plot_covariance

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

モデリングの準備

データの読み込み

サンプルコードのデータを読み込みます。

### データの読み込み ◆データファイル11.5 data-ZIP.txt
# Sex:性別(0:男性, 1:女性), Sake:飲酒(0:飲まない, 1:飲む), Age:年齢,
# Y:来店回数（目的変数）

data = pd.read_csv('./data/data-ZIP.txt')
print('data.shape: ', data.shape)
display(data.head())

【実行結果】

軽くデータの外観を確認します。
目的変数 Y のヒストグラムを描画します。

### Yのヒストグラムの描画

# ビン幅の設定
bins = np.arange(data['Y'].min() - 0.5, data['Y'].max() + 0.5)
# ヒストグラムの描画
sns.histplot(data=data, x='Y', bins=bins, ec='white', kde=True)
# 修飾
plt.xticks(bins + 0.5)
plt.grid(lw=0.5);

【実行結果】
来店回数$${Y=0}$$が異常に多いです！
0が過剰です！ゼロ過剰です（←これが言いたかった）

質的変数vs目的変数の箱ひげ図を描画します。

### 箱ひげ図の描画

# タイトルに使用する文章
col_names = ['性別(0:男性, 1:女性)', '飲酒習慣(0:飲まない, 1:飲む)']
# 描画領域の設定
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
# axの数だけ描画を繰り返し処理
for i, col in enumerate(data.columns[:2]):
    # 箱ひげ図の描画
    sns.boxplot(data=data, y='Y', hue=col, palette='Pastel1', ax=ax[i])
    # 修飾
    ax[i].set_title(f'説明変数: {col_names[i]},\n目的変数:$Y$ 来店回数')

【実行結果】
何らかの相関がありそうです。

量的変数と目的変数の散布図を描画します。

### 散布図の描画

# 散布図の描画
sns.scatterplot(data=data, x='Age', y='Y', hue='Sake', style='Sex', s=80,
                alpha=0.5)
# 修飾
plt.title(f'説明変数: 年齢, 目的変数:$Y$ 来店回数')
plt.grid(lw=0.5);

【実行結果】
お酒を飲まない人（Sake=0）の来店回数が０が多いです。

重回帰分析

テキストにならって重回帰分析を行います。
statsmodels の ols を用います。

### 重回帰分析 statsmodels ◆テキスト114ページの重回帰
lm_model = smf.ols(formula='Y ~ Sex + Sake + Age', data=data)
result = lm_model.fit()
display(result.summary())

【実行結果】
テキストの通り、決定係数（R-squared）が低いです。

11.3.1 解析の目的とデータの分布の確認

散布図行列の描画

テキスト図11.4の散布図行列を描画します。

### 散布図行列の描画 ◆図11.4
# スピアマンの順位相関係数に応じた楕円の描画処理を追加した
# 凡例非表示・・・描画関数の引数に legend=None を追加する

## 描画領域の指定
fig, ax = plt.subplots(4, 4, figsize=(10, 10))
ax = ax.ravel() # １次元でaxesを指定したいので

## 番地0,0：ヒストグラムの描画（棒グラフを使用）
bar_Sex = data.Sex.value_counts().sort_index()
sns.barplot(ax=ax[0], x=bar_Sex.index, y=bar_Sex, hue=bar_Sex.index,
            palette='tab10', alpha=0.5, ec='white')
ax[0].set(ylabel='Sex', xlabel=None)
ax[0].grid(lw=0.5)

## 番地1,0：散布図？
mul = 40
tmp_data = data.groupby(['Sex', 'Sake'])['Y'].count().to_frame().reset_index()
sns.scatterplot(ax=ax[4], data=tmp_data, x='Sex', y='Sake', hue='Sex', size='Y',
                sizes=[x * mul for x in tmp_data.Y.sort_values()], alpha=0.5,
                palette='tab10', legend=None)
for i in range(len(tmp_data)):
    ax[4].text(s=tmp_data.loc[i, 'Y'], fontsize=16,
               x=tmp_data.loc[i, 'Sex'], y=tmp_data.loc[i, 'Sake'],
               va='center', ha='center')
ax[4].set(xlabel=None, xlim=(-0.5, 1.5), ylim=(-0.5, 1.5), xticks=(0, 1),
          yticks=(0, 1))
ax[4].grid(lw=0.5)

## 番地1,1：ヒストグラムの描画（棒グラフを使用）
bar_Sake = data.Sake.value_counts().sort_index()
sns.barplot(ax=ax[5], x=bar_Sake.index, y=bar_Sake, hue=bar_Sake.index,
            palette='tab10', alpha=0.5, ec='white')
ax[5].set(ylabel='Sake', xlabel=None)
ax[5].grid(lw=0.5)

## 番地2,0：箱ひげ図＋スウォームプロットの描画
sns.boxplot(ax=ax[8], x=data.Sex, y=data.Age, hue=data.Sex, fill=False,
            legend=None)
sns.stripplot(ax=ax[8], x=data.Sex, y=data.Age, hue=data.Y, size=5,
              palette='Reds', legend=None)
ax[8].set(xlabel=None)
ax[8].grid(lw=0.5)

## 番地2,1：箱ひげ図＋スウォームプロットの描画
sns.boxplot(ax=ax[9], x=data.Sake, y=data.Age, hue=data.Sake, fill=False,
            legend=None)
sns.stripplot(ax=ax[9], x=data.Sake, y=data.Age, hue=data.Y, size=5,
              palette='Reds', legend=None)
ax[9].set(xlabel=None)
ax[9].grid(lw=0.5)

## 番地2,2：ヒストグラムの描画
sns.histplot(ax=ax[10], data=data, x='Age', bins=10, kde=True, ec='white',
             label='Age')
ax[10].set(xlabel=None, ylabel=None)
ax[10].grid(lw=0.5)
ax[10].legend()

## 番地3,0：箱ひげ図＋スウォームプロットの描画
sns.boxplot(ax=ax[12], x=data.Sex, y=data.Y, hue=data.Sex, fill=False,
            legend=None)
sns.stripplot(ax=ax[12], x=data.Sex, y=data.Y, hue=data.Y, size=5,
              palette='Reds', legend=None)
ax[12].grid(lw=0.5)

## 番地3,1：箱ひげ図＋スウォームプロットの描画
sns.boxplot(ax=ax[13], x=data.Sake, y=data.Y, hue=data.Sake, fill=False,
            legend=None)
sns.stripplot(ax=ax[13], x=data.Sake, y=data.Y, hue=data.Y, size=5,
              palette='Reds', legend=None)
ax[13].grid(lw=0.5)

## 番地3,2：散布図の描画
sns.scatterplot(ax=ax[14], data=data, x='Age', y='Y', hue='Y', palette='Reds',
                legend=None)
ax[14].set(ylabel=None)
ax[14].grid(lw=0.5)

## 番地3,3：ヒストグラムの描画
sns.histplot(ax=ax[15], data=data, x='Y', bins=10, kde=True, ec='white',
             label='Y')
ax[15].set(ylabel=None)
ax[15].grid(lw=0.5)
ax[15].legend()

## スピアマンの順位相関係数を上三角のaxesに表示
# 列名をリスト化
cols = ['Sex', 'Sake', 'Age', 'Y']
# 楕円描画関数の引数
mean = [0, 0]
std = [1, 1]
# 列名の組み合わせ 行i,列j ごとにテキスト表示を繰り返す
for i, col1 in enumerate(cols):
    for j, col2 in enumerate(cols):
        # 上三角の位置は 行i < 列j のとき
        if i < j:
            ## 描画準備
            # axesの番号を取得
            pos = i * len(cols) + j
            # 枠線等を削除
            ax[pos].set_axis_off()
            ## スピアマンの順位相関係数の表示
            # スピアマンの順位相関係数の算出
            corr, pval = stats.spearmanr(data[col1], data[col2])
            # 相関係数をテキスト表示：中央表示に関連する引数: x,y,va,ha,transform
            ax[pos].text(x=0.5, y=0.5, s=round(corr * 100), fontsize=30,
                         va='center', ha='center', transform=ax[pos].transAxes)
            ## 相関係数に応じた楕円の描画
            # 共分散の算出
            cov = [[std[0]**2, std[0]*std[1]*corr],
                   [std[0]*std[1]*corr, std[1]**2]]
            # axesの再定義（pltで定義）
            plt.subplot(4, 4, pos+1)
            # 相関係数に応じた楕円の描画（plt）
            # https://github.com/rlabbe/filterpy/blob/master/filterpy/stats/stats.py
            plot_covariance(mean=mean, cov=cov, show_center=False, ec='tab:red',
                            fc='lightpink', alpha=0.2)
            plt.xlim(-1.2, 1.2)
            plt.ylim(-1.2, 1.2)
            
# 全体修飾
plt.tight_layout();

【実行結果】
上三角のスピアマンの順位相関係数に楕円による相関イメージを追加しました！

11.3.4 Stanで実装

PyMCのモデル定義

PyMCでモデル式11-7を実装します。
データの前処理です。
説明変数$${X}$$を整えます。

### 説明変数 x_const の作成
# 定数１項, Sex, Sake, Ageを１つのデータフレームx_constに格納
x_const = pd.concat([pd.DataFrame({'const': np.ones(len(data), dtype=int)}),
                     data.iloc[:, :3]], axis=1)
# Ageの値を1/10に変換
x_const['Age'] = x_const['Age'] / 10
display(x_const)

【実行結果】

モデルの定義です。

### モデルの定義 ◆モデル式11-7 model11-7.stan

with pm.Model() as model:
    
    ### データ関連定義
    ## coordの定義
    model.add_coord('data', values=data.index, mutable=True)
    model.add_coord('coef', values=[1, 2, 3, 4], mutable=True)
    ## dataの定義
    # 目的変数 Y
    Y = pm.ConstantData('Y', value=data['Y'].values, dims='data')
    # 説明変数 X
    X = pm.ConstantData('X', value=x_const.values, dims=('data', 'coef'))

    ### 事前分布
    b1 = pm.Uniform('b1', lower=-8, upper=8, dims='coef')
    b2 = pm.Uniform('b2', lower=-8, upper=8, dims='coef')

    ### ZIP分布のパラメータ
    # 来店確率 q
    q = pm.Deterministic('q', pm.invlogit(pt.dot(X, b1)), dims='data')
    # 平均 λ
    lam = pm.Deterministic('lam', pt.dot(X, b2), dims='data')

    ### 尤度関数 ゼロ過剰ポアソン分布(ZIP分布)
    obs = pm.ZeroInflatedPoisson('obs', psi=q, mu=lam, observed=Y, dims='data')

モデルの定義内容を見ます。

### モデルの表示
model

【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)

【実行結果】

MCMCの実行と収束確認

MCMCを実行します。

### 事後分布からのサンプリング 25秒 ◆run-model5-5.R
with model:
    idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.9999,
                      nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

Pythonで事後分布からのサンプリングデータの確認を行います。
Rhatの確認から。
テキストの収束条件は「chainを3以上にして$${\hat{R}<1.1}$$のとき」です。

### r_hat>1.1の確認
# 設定
idata_in = idata         # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
収束条件を満たしています。

事後統計量を表示します。

### 推論データの要約統計情報の表示
var_names = ['b1', 'b2']
pm.summary(idata, hdi_prob=0.95, var_names=var_names, round_to=3)

【実行結果】

### 推論データの要約統計情報の表示
var_names = ['q', 'lam']
pm.summary(idata, hdi_prob=0.95, var_names=var_names, round_to=3)

【実行結果】

トレースプロットを描画します。
パラメータの一部です。

### トレースプロットの表示
var_names = ['b1', 'b2']
pm.plot_trace(idata, compact=False, var_names=var_names)
plt.tight_layout();

【実行結果】

11.3.5 推定結果の解釈

事後分布の要約統計量を算出します。
算出関数を定義します。

### mean,sd,2.5%,25%,50%,75%,97.5%パーセンタイル点をデータフレーム化する関数の定義
def make_stats_df(y):
    probs = [2.5, 25, 50, 75, 97.5]
    columns = ['mean', 'sd'] + [str(s) + '%' for s in probs]
    quantiles = pd.DataFrame(np.percentile(y, probs, axis=0).T, index=y.columns)
    tmp_df = pd.concat([y.mean(axis=0), y.std(axis=0), quantiles], axis=1)
    tmp_df.columns=columns
    return tmp_df

要約統計量を算出します。

## 要約統計量の算出・表示
b1_samples = pd.DataFrame(
            idata.posterior.b1.stack(sample=('chain', 'draw')).data.T,
            columns=[f'b1[{i+1}]' for i in range(4)])
b2_samples = pd.DataFrame(
            idata.posterior.b2.stack(sample=('chain', 'draw')).data.T,
            columns=[f'b2[{i+1}]' for i in range(4)])
param_samples = pd.concat([b1_samples, b2_samples], axis=1)
display(make_stats_df(param_samples).round(2))

【実行結果】
テキスト２１８ページに掲載の各パラメータの要約と比べてみると、b1 はテキストの結果と近い感じですが、b2 はテキストと乖離しています。

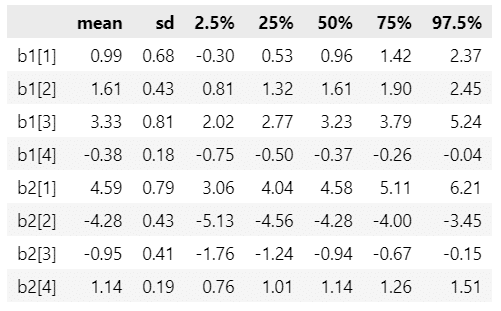
ただ、テキストとプラス・マイナスの符号が同じなので、テキストの次の分析内容はこのモデルの推論値を使っても言えると思います。

来店確率が高いのは女性（b1[2]が正）・お酒を飲み（b1[3]が正）・年齢が低い（b1[4]が負）人です。
リピーターになって多数来店するのは男性（b2[2]が負）・お酒を飲まず（b2[3]が負）・年齢が高い（b2[4]が正）人です。

テキストの記述を一部改変して引用

パラメータ$${q}$$と$${\lambda}$$の順位相関係数を計算してみます。
テキストの run-model11-7.R で計算されるものです。

### パラメータλ（リピート回数）とq（来店確率）の
### スピアマン相関係数の算出と中央値・ベイズ信用区間の算出 ◆テキスト218ページ

# 推論データからλとqのMCMCサンプルデータを取り出し
lam_samples = idata.posterior.lam.stack(sample=('chain', 'draw'))
q_samples = idata.posterior.q.stack(sample=('chain', 'draw'))

# リストの初期化
spearman_r = []

# MCMCサンプルデータの数（4000）だけスピアマン相関係数の算出を繰り返し処理
for i in range(lam_samples.shape[1]):
    # 200人分のサンプルデータでスピアマン相関係数を算出
    corr, _ = stats.spearmanr(lam_samples[:, i], q_samples[:, i])
    # リストに追加
    spearman_r.append(corr)

# 統計量の算出・表示
display(make_stats_df(pd.DataFrame({'spearman': spearman_r})).round(2))

【実行結果】
テキストの中央値と95%ベイズ信頼区間は$${-0.65\ [-0.80,\ -0.47]}$$です。
このモデルでは$${-0.65\ [-0.82,\ -0.48]}$$であり、テキストと近い結果になりました。
来店確率が高さとリピーターの来店回数の多さとの間には負の相関（$${-0.65}$$）があると言えそうです。

11.3 節は以上です。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

いいなと思ったら応援しよう！

この記事が参加している募集

#新生活をたのしく

47,060件