8-6 母平均の差の検定 ～ 対応のない２標本の母平均の差のｔ検定（等分散）

今回の統計トピック

統計的仮説検定のトピック「対応のない２標本の母平均の差の$${t}$$検定」を深掘りします。
$${t}$$検定はメジャーなので、ツールも充実しています。
EXCEL、Pythonに加えて、無料ツールもご紹介いたします！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

問題を解いて、知る・実践する

---

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
１標本の母平均の差の$${t}$$検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ

検定の分野
問6 母平均の差の検定（プロ野球チームの年間入場者数）

試験実施年月
統計検定2級 2018年6月 問12（回答番号24）

📕公式テキスト：4.4.1 母平均の差の検定　母分散が未知で等しい場合（152ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件から、対応のない２標本の母平均の差の検定に用いる$${t}$$値を求めます。

【条件】
・２つの母平均の差に関する$${t}$$検定を行います。
・２つの標本は独立で同一の分布に従います。
・２つの母分散は等しいです。
・２つの標本の平均は、233.7 と 185.3 です。
・２つの標本の偏差平方和は、13549 と 7763 です。

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

• 「対応のない２標本の母平均の差の検定」（母分散が未知で等しい）です。

• 帰無仮説は「２つの母平均の差は０である」です。

• 検定統計量は$${t}$$です。

• 母分散が未知であり等しいので、「プールした分散」を計算して、検定統計量の算出をします。

この問題の統計的仮説検定の概要を図示します。

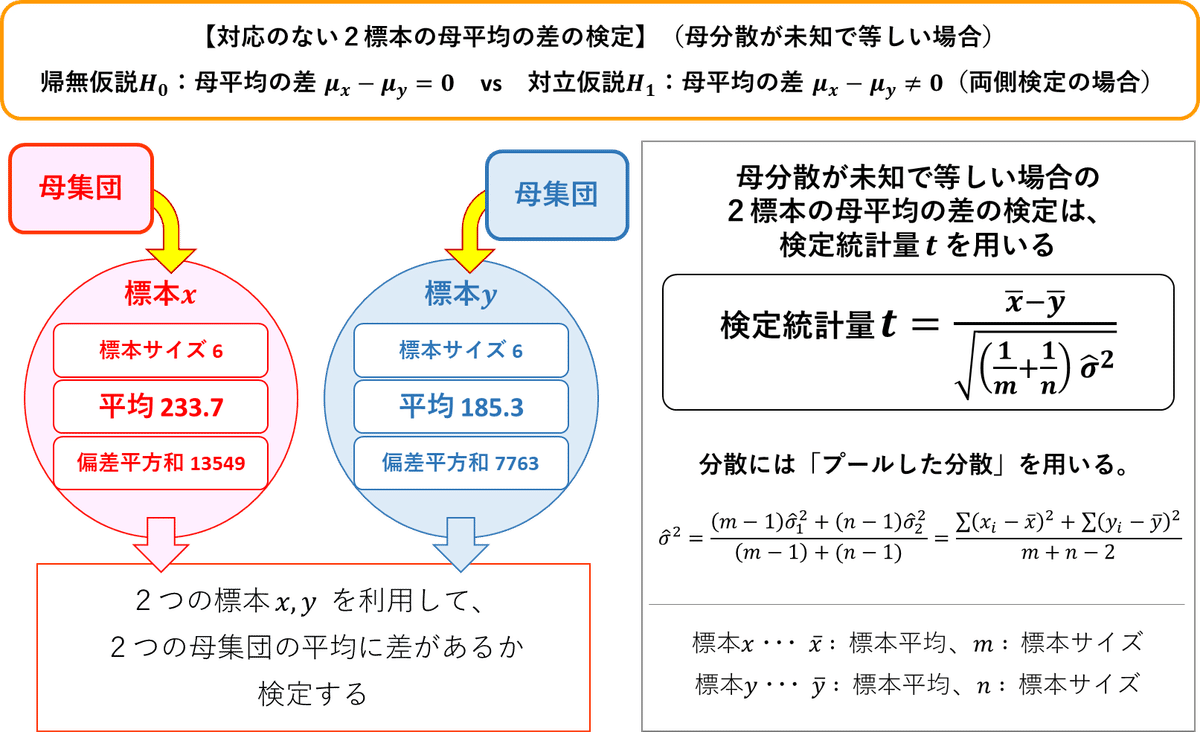
統計的仮説検定の手段

今回は、①手計算、②EXCEL、③Python の３つの手段で検定を実施いたします。

---

手計算で検定

帰無仮説が正しいと仮定するときの検定統計量 $${t}$$ を計算します。
計算結果の値を「$${t}$$値」と呼びます。
この問題で「帰無仮説が正しいと仮定する」とは、「母平均の差$${\mu_x-\mu_y=0}$$である」と仮定することです。

検定統計量$${t}$$の計算式は次のとおりです。
なお、この検定統計量$${t}$$は自由度$${m+n-1}$$の$${t}$$分布に従います。

■公式　検定統計量$${t}$$
$${t=\cfrac{\bar{x}-\bar{y}}{\sqrt{\left(\cfrac{1}{m}+\cfrac{1}{n} \right)\hat{\sigma}^2}} \sim t(m+n-2)}$$

■公式　プールした分散
$${\hat{\sigma}^2=\cfrac{(m-1)\hat{\sigma}^2_x+(n-1)\hat{\sigma}^2_y}{(m-1)+(n-1)} = \cfrac{\sum (x_i-\bar{x})^2 + \sum (y_i-\bar{y})^2 }{m+n-2}}$$

・$${\bar{x}, \bar{y}}$$：標本$${x,y}$$の標本平均
・$${m, n}$$：標本$${x,y}$$の標本サイズ
・$${\sum (x_i-\bar{x})^2}$$：標本$${x}$$の偏差平方和
・$${\sum (y_i-\bar{y})^2}$$：標本$${y}$$の偏差平方和

いろいろな紙に何かを書く人のイラスト（男性）：「いらすとや」さんより

■プールした分散
まず、プールした分散を計算します。
問題文で与えられた標本サイズ$${m=n=6}$$、偏差平方和$${13549, 7763}$$を用いてプールした分散$${\hat{\sigma}^2}$$を計算します。

$$
\begin{align*}
\hat{\sigma}^2&= \cfrac{\sum (x_i-\bar{x})^2 + \sum (y_i-\bar{y})^2 }{m+n-2} \\
 \\
&=\cfrac{13549+7763}{6+6-2} \\
 \\
&=\cfrac{21312}{10} \\
 \\
&=2131.2 \\
\end{align*}
$$

数式にすると難解な雰囲気になるので、ここはひとつ、日本語化しましょう。
$${プールした分散=\cfrac{標本1の偏差平方和+標本2の偏差平方和}{標本サイズの合計-2}}$$です。
２つの標本を合算して不偏分散を計算しています。
これは、１変数の不偏分散$${\cfrac{偏差平方和}{標本サイズ-1}}$$の分母同士を足して、分子同士を足して、不偏分散を平均化する感じです！

水泳のイラスト「プール」：「いらすとや」さんより

■検定統計量$${\boldsymbol{t}}$$ 
続いて、検定統計量$${t}$$を計算します。
問題文で与えられた標本平均$${\bar{x}=233.7}$$、$${\bar{y}=185.3}$$、標本サイズ$${m=n=6}$$、計算したプールした分散$${2131.2}$$を用いて検定統計量$${t}$$を計算します。

$$
\begin{align*}
t&=\cfrac{\bar{x}-\bar{y}}{\sqrt{\left(\cfrac{1}{m}+\cfrac{1}{n} \right)\hat{\sigma}^2}} \\
 \\
&=\cfrac{233.7-185.3}{ \sqrt{(1/6+1/6)\times 2131.2}} \\
 \\
&=\cfrac{48.4}{\sqrt{710.4}} \\
 \\
&=1.815 \cdots \\
 \\
&\fallingdotseq 1.82
\end{align*}
$$

$${t}$$値は$${1.82}$$です。

手計算は以上となります。

■補足　標本平均の差の分散
検定統計量$${t}$$の計算に用いられる標本平均の差の分散に関する補足です。

独立に同一の分布に従う２標本$${x,y}$$（標本サイズ$${m,n}$$、分散$${\sigma^2}$$）について、標本平均の差を$${d=\bar{x}-\bar{y}}$$と表しましょう。

$${\bar{x}}$$の分散$${V[\bar{x}]}$$は$${\sigma^2/m}$$、$${\bar{y}}$$の分散$${V[\bar{y}]}$$は$${\sigma^2/n}$$です。
標本平均の差$${d}$$の分散$${V[d]}$$は、次のように計算でき、$${(1/m+1/n)\sigma^2}$$になります。

（計算過程）
$${V[d]=V[\bar{x}-\bar{y}]=V[\bar{x}]+V[-1 \times \bar{y}]=V[\bar{x}]+(-1)^2 \times V[\bar{y}]=V[\bar{x}]+V[\bar{y}]=\sigma^2/m+\sigma^2/n=(1/m+1/n)\sigma^2}$$

■帰無仮説は棄却できるの？

出題されていないですが、統計的仮説検定を続けましょう！
$${t}$$値$${1.82}$$、自由度$${m+n-2=10}$$をもとにして、帰無仮説を棄却できるかどうか確認します。
両側検定とし、有意水準は$${5\%}$$と$${10\%}$$の２ケースを考えます。

$${t}$$分布のパーセント点表を見ます。

有意水準$${5\%}$$の棄却域は$${|t|>2.228}$$です。
有意水準$${10\%}$$の棄却域は$${|t|>1.812}$$です。

$${t}$$値$${=1.82}$$が棄却域に含まれる場合、帰無仮説を棄却できます。
有意水準$${5\%}$$の場合、$${|t|<2.228}$$となり、$${t}$$値が棄却域に含まれないので、帰無仮説は棄却されません。
有意水準$${10\%}$$の場合、$${|t|>1.812}$$となり、$${t}$$値が棄却域に含まれるので、帰無仮説は棄却されます。

---

EXCELで検定

EXCELで対応のない２標本の母平均の差の$${t}$$検定を行います。
①計算シートを利用する方法と、②分析ツール機能を利用する方法を紹介いたします。

①計算シートを利用

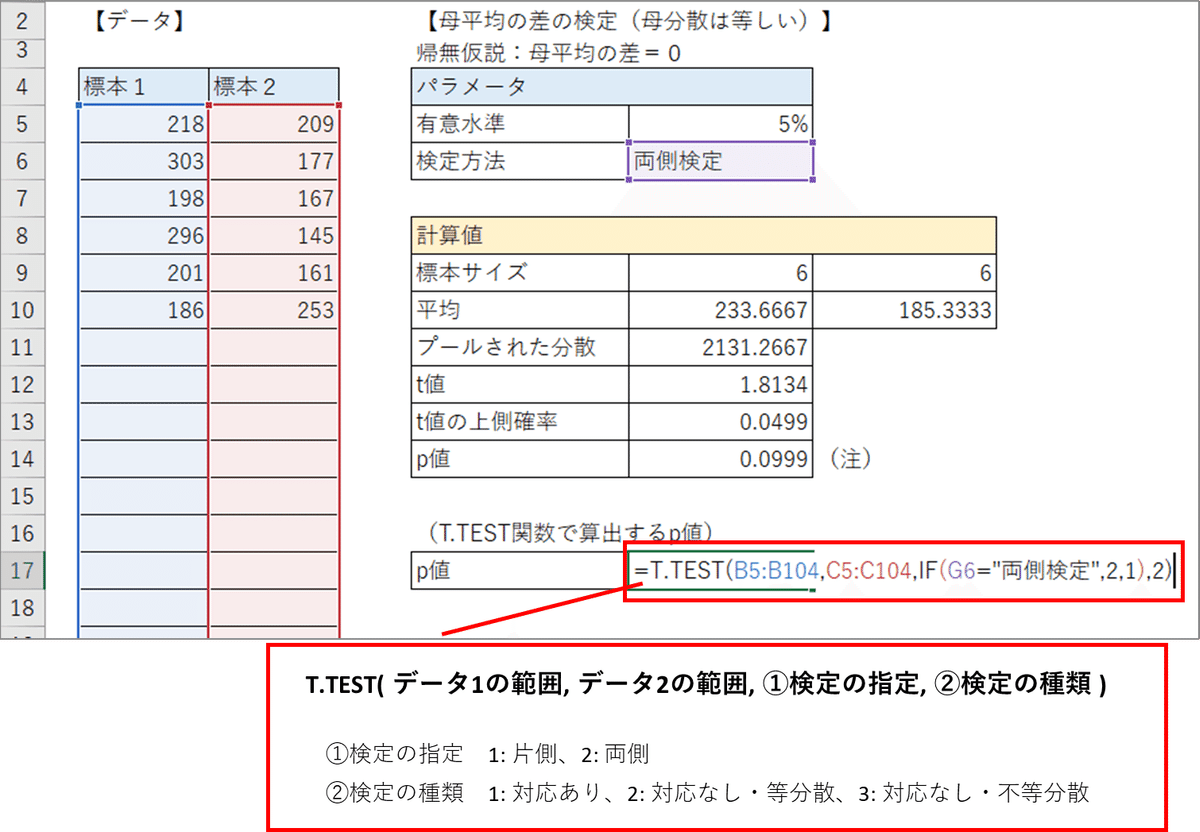
計算シートの全体像です。
【データ】エリアに２つの標本データを登録します。
そしてパラメータに有意水準と検定方法を入力します。

このシートは、T.TEST 関数を除いて、特別な関数を利用していません。
検定統計量$${t}$$の公式どおりに計算式を設定しており、$${t}$$値の上側確率は$${t}$$分布の関数 T.DIST.RT 関数を利用しています。

■統計的仮説検定の実行

シートのデータエリアに予め値をセットしています。
このデータとパラメータから$${t}$$値、$${p}$$値を自動計算します。
有意水準$${5\%}$$、両側検定で実行しましょう。

$${t}$$値$${=1.8134}$$、$${p}$$値$${0.0999}$$になりました。
$${p}$$値が有意水準を上回っており、帰無仮説は棄却されません。

■ T.TEST 関数

EXCELには「２標本の母平均の差の$${t}$$検定」の$${p}$$値を計算できる「 T.TEST 関数」があります。
便利です。

②分析ツールを利用

EXCELの「分析ツール」には、次のような$${t}$$検定の分析表を作成する機能があります。
基本統計量、プールされた分散、$${t}$$値、$${p}$$値が整然と表示されます。
簡単な操作で綺麗な分析表を得られるので、使い勝手がよさそうです！

■ 分散ツールの利用方法

１．データ分析メニュー

予め２つの標本データをEXCELに入力しておきます。
メニューより、「データ」（①）＞「データ分析」（②）を選択します。
「データ分析」画面が表示されます。

２．「データ分析」画面

対応のない２標本の母平均の差の$${t}$$検定（分散が等しい）を行う場合には、「ｔ検定：等分散を仮定した２標本による検定」（③）を選択して、「ＯＫボタン」（④）をクリックします。
「ｔ検定：等分散を仮定した２標本による検定」画面が表示されます。

３．「ｔ検定：等分散を仮定した２標本による検定」画面

変数１の入力範囲（⑤）、変数２の入力範囲（⑥）に、２つの標本データの範囲を設定します。
出力オプションで分析表の出力先を指定します。
今回は、データのすぐ横のセル（⑦）を指定しました。
「ＯＫボタン」（⑧）をクリックします。

４．分析表の表示

「出力先」で指定した場所に分析表が表示されました。

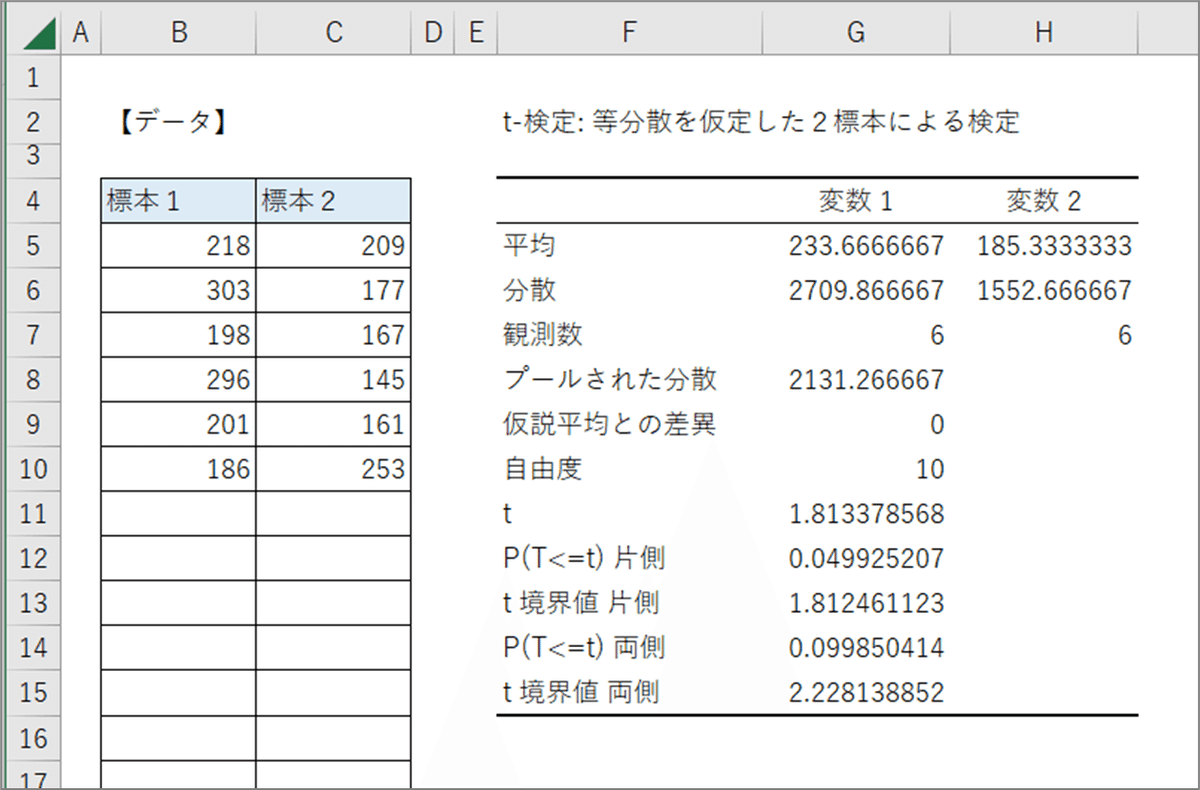
おっと忘れるところでした。

解答の$${t}$$値は$${1.81}$$です。
問題集の解答$${1.82}$$とは端数処理等の影響で少し異なっているようです。

EXCELは以上となります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

8-6_母平均の差の検定.xlsx

17.4 KB

ファイルダウンロードについて

ダウンロード

---

Pythonで検定

Pythonで対応のない２標本の母平均の差の$${t}$$検定（等分散）を行います。
今回は、５種類の方法で検定しちゃいます！

インポート

import numpy as np
from scipy import stats
from statsmodels.stats.weightstats import ttest_ind
import pingouin as pg

※ pingouin のインストール方法

# pipでインストールする場合
pip install pingouin

# anaconda環境にインストールする場合
conda install -c conda-forge pingouin

データの準備

問題集のデータを入力します。

# データの入力 data_cen:セ・リーグ、data_pac:パ・リーグ
data_cen = np.array([218, 303, 198, 296, 201, 186])
data_pac = np.array([209, 177, 167, 145, 161, 253])

では、検定を実施しましょう。

① 検定統計量$${\boldsymbol{t}}$$の公式どおりの計算 
データの標本サイズ、平均、偏差平方和を用いて$${t}$$値を算出します。
scipy.stats を利用して、自由度$${m+n-2}$$の$${t}$$分布の上側確率＝$${p}$$値を取得します。

# 標本サイズ、平均、偏差平方和の算出
num_cen = data_cen.shape[0]
num_pac = data_pac.shape[0]
mean_cen = data_cen.mean()
mean_pac = data_pac.mean()
ssd_cen = ((data_cen - mean_cen)**2).sum()
ssd_pac = ((data_pac - mean_pac)**2).sum()

# t値の算出：検定統計量tの公式どおりの計算
t_value = (mean_cen - mean_pac) / np.sqrt(
          (1/num_cen + 1/num_pac) * ( (ssd_cen + ssd_pac) / (num_cen + num_pac - 2) ) 
           )
print(f't値: {t_value:.3f}')

# p値の算出：scipy.statsの t.sf でt分布の上側確率を取得
print(f'p値: {stats.t.sf(t_value, df=num_cen+num_pac-2) * 2:.3f}')

①の計算結果

② 公式問題集の解答どおりの計算
公式問題集で所与の平均、偏差平方和の値を用いて$${t}$$値を計算します。

# 設定（所与の値を利用）
mean_cen = 233.7
mean_pac = 185.3
ssd_cen = 13549
ssd_pac = 7763

# t値の算出：検定統計量tの公式どおりの計算
t_value = (mean_cen - mean_pac) / np.sqrt(
          (1/num_cen + 1/num_pac) * ( (ssd_cen + ssd_pac) / (num_cen + num_pac - 2) ) 
           )
print(f't値: {t_value:.3f}')

# p値の算出：scipy.statsの t.sf でt分布の上側確率を取得
print(f'p値: {stats.t.sf(t_value, df=num_cen+num_pac-2) * 2:.3f}')

②の計算結果

①の公式利用の場合と比べて、$${t}$$値が若干大きく、$${p}$$値は若干小さいです。
平均、偏差平方和の端数処理が影響していると思われます。

③ scipy.stats の ttest_ind を利用
ここからは、$${t}$$検定専用の機能を利用します。
シンプルなコードで実行できます。

ind=対応のない２標本の平均の差の$${t}$$検定を行って、$${t}$$値、$${p}$$値を取得できます。
等分散の場合に加えて、不等分散（Welchのt検定）も実施可能です。

t_value, p_value = stats.ttest_ind(data_cen, data_pac,
        equal_var=True,          # 等分散:True、不等分散・Welchのt検定:False
        alternative='two-sided') # 両側検定:two-sided、片側＞:greater、片側＜:less

print(f't値: {t_value:.3f},  p値:{p_value:.3f}')

③の計算結果

④ statsmodels の ttest_ind を利用
ind=対応のない２標本の平均の差の$${t}$$検定を行って、$${t}$$値、$${p}$$値、自由度を取得できます。
等分散の場合に加えて、不等分散（Welchのt検定）も実施可能です。
scipy.stats とよく似ていますが、引数名や引数の値が微妙に異なります。

t_value, p_value, df = ttest_ind(data_cen, data_pac,
        alternative='two-sided',  # 両側検定:two-sided、片側＞:greater、片側＜:less
        usevar='pooled',          # 等分散:pooled、不等分散・Welchの検定:unequal
        value=0)                  # 帰無仮説の母平均の差の値

print(f't値: {t_value:.3f},  p値:{p_value:.3f}')

④の計算結果

⑤ pingouin の ttest を利用
計算結果をpandasのデータフレーム形式で返してくれます。
$${t}$$値（T）、$${p}$$値（p-val）に加えて、平均の差の信頼区間（CI95%）、cohen効果量（cohen-d）、対立仮説のベイズ因子（BF10）、検定で達成できる検出力（power）を表示します。

pg.ttest(data_cen, data_pac,
         paired=False,           # 対応のある２標本:True、対応のない２標本:False
         correction=False,       # Welchのt検定:True、studentのt検定:False
         alternative='two-sided' # 両側検定:two-sided、片側＞:larger、片側＜:smaller
         ).round(3)

⑤の計算結果

まとめますと、$${t}$$値の解答は$${1.813}$$です。
２標本の母平均の差の$${t}$$検定については、Pythonのさまざまな統計処理ライブラリに専用機能が備わっています。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

8-6_母平均の差の検定.ipynb

8.54 KB

ファイルダウンロードについて

ダウンロード

以上で終了です。
お疲れ様でした。

解答

④ です。

難易度　ふつう

・知識：対応のない２標本の母平均の差の$${t}$$検定（母分散が未知で等しい場合）、プールした分散
・計算力：数式組み立て（中）、電卓（低）
・時間目安：1分

---

おわりに

２標本の母平均の差の$${t}$$検定は、EXCELもPython も専用機能が整っており、サクッと計算できます。
お手元にデータが２つあって、２つの平均値に差があるかどうかを調べたいときはぜひ、EXCELやPython でサクッと！

そして、$${t}$$検定は「フリーの統計解析ツール」でサクッと実施できます。

番外編

ということで、５つの無料ツールで、対応のない２標本の母平均の差の検定（等分散）を試してみました。

１．HAD（EXCEL上で稼働）

HAD：フリーの統計プログラム | Sunny side up!

HADの分析結果表示（例）

２．統計解析ソフトウェア（EXCEL上で稼働）

フリーソフトウェアの概要 :: 【公式】株式会社アイスタット｜統計分析研究所

統計解析ソフトウェアの分析結果表示（例）

３．jamovi　：海外製、日本語表示に対応しています

jamovi - open statistical software for the desktop and cloud

janoviの分析結果表示（例）

４．JASP　：海外製、日本語表示に対応しています

JASP - A Fresh Way to Do Statistics

JASPの分析結果表示（例）

５．College Analysis　：多機能です

社会システム分析用ソフトウェアについて

Collage Analysisの分析結果表示（例）

お好みのツールを見つけて、日々のデータ分析を楽しんでください！

最後までお読みいただきまして、ありがとうございました。

---

のんびり統計シリーズの記事

次の記事

前の記事

目次