
時系列分析入門【第5章 その2】コヒーレンス・クロスウェーブレット解析・位相差・レイリー検定をPythonで実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第5章「時系列データ同士の関係の評価」のRスクリプトをお借りして、Python で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは、周波数等に関連する次のトピックです。
・コヒーレンス
・ウェーブレットクロススペクトル解析
・位相差の評価
・イベント周期の安定性
周波数・・・、なんだか難しそうなテーマです。
一部のコードはテキスト通りの結果を得られませんでした。
さあ、時系列分析を楽しんでいきましょう!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第5章 時系列データ同士の関係の評価
この記事は「5.4 周波数領域での類似度」「5.5 位相差の評価」「5.6 イベント周期の安定性」を実践いたします。
インポート
この章で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# Rデータセット読み取り
import statsmodels.api as sm
import rdata
# WEBアクセス/googleトレンド
import requests
from pytrends.request import TrendReq
# Zipファイル操作
import zipfile
# データ前処理
from sklearn.preprocessing import StandardScaler
# 日付処理
from datetime import datetime
from dateutil import tz
# DTW処理
# pip install dtw_python
from dtw import dtw
# 信号処理
from scipy.signal import coherence, periodogram
import scipy.signal as signal
# 方向データの統計処理
# pip install pingouin
import pingouin as pg
# 階層的クラスタリング、デンドロビウム描画
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
# VAR・AR
from statsmodels.tsa.vector_ar.var_model import VAR
from statsmodels.tsa.ar_model import AutoReg
# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】パッケージのインストール
利用環境に応じてパッケージをインストールしてください。
以下はインストールの参考コードです。
### インストール
## dtw-python
# anaconda
conda install -c conda-forge dtw-python
# pip
pip install dtw-python
## pingouin
# anaconda
conda install -c conda-forge pingouin
# pip
pip install pingouin
コヒーレンス
テキスト「5.4.1 コヒーレンス」のコードを実践します。
ただ正直なところ、個人的によく分からない領域です。
淡々とテキストをこなす感じで記述いたします。
■ $${x(t)}$$のパワースペクトル
※時系列データ$${x(t)}$$のフーリエ変換を$${X(f)}$$とする
$$
P_x(f) = X(f)^{*}X(f) = |X(f)|^2
$$
※$${*}$$は複素共役、$${P_x(f)}$$は周波数ごとの波の強さ
■ 2つの時系列信号$${x(t), y(t)}$$のクロススペクトル$${C_{xy}(f)}$$
$$
C_{xy}(f) = X(f)^{*}Y(f) = |C_{xy}(f)| e^{i\theta(f)}
$$
※$${|C_{xy}()f|}$$は振幅の大きさ、$${\theta(f)}$$は$${x}$$を基準とした2つの時系列データ間の位相差
■ コヒーレンス$${Coh}$$
$$
Coh^2_{xy}(f) = \cfrac{|C_{xy}(f)|^2}{{P_x(f)P_y(f)}}, \quad 0 \leq Coh_{xy}(f) \leq 1
$$
① 信号の作成とパワースペクトルの算出
テキストの作成方法をお借りして、サンプリングレート1000Hz、0.25秒のデータを作成します。
### 信号の作成
# 1000Hzのサンプリングレートで0.25秒のデータを作成
t = np.arange(0, 0.25, 0.001)
# xには80Hzのcos波形と120Hzのsin波形を設定
x = np.cos(2*np.pi*80*t) + 0.5*np.sin(2*np.pi*120*t)
# yには80Hzのsin波形と200Hzのsin波形を設定
y = np.sin(2*np.pi*80*t) + 0.8*np.sin(2*np.pi*200*t)
# パワースペクトルの算出 numpyのfft.fftでフーリエ変換
X = np.fft.fft(x, 250) # xをフーリエ変換
Y = np.fft.fft(y, 250) # yをフーリエ変換
frequency = 1000/250 * np.arange(0, 125) # ナイキスト周波数の範囲を設定
Pxx = X.conjugate() * X / 250 # xのパワースペクトル
Pyy = Y.conjugate() * Y / 250 # yのパワースペクトル【実行結果】なし
② 信号とパワースペクトルの描画
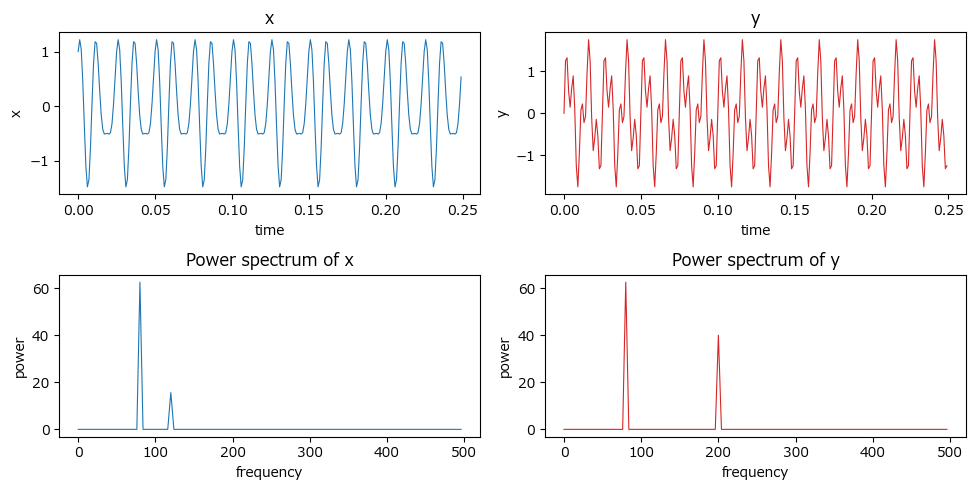
信号データ x、y とパワースペクトル Pxx、Pyy を描画します。
テキストの図5.9の上段・中段に相当します。
### パワースペクトルの描画 ※図5.9上段・中段に相当
# 描画領域
plt.figure(figsize=(10, 5))
# x(t)の描画
ax = plt.subplot(221)
ax.plot(t, x, lw=0.8, color='tab:blue')
ax.set(title='x', xlabel='time', ylabel='x')
# y(t)の描画
ax = plt.subplot(222)
ax.plot(t, y, lw=0.8, color='tab:red')
ax.set(title='y', xlabel='time', ylabel='y')
# パワースペクトルPxxの描画
ax = plt.subplot(223)
ax.plot(frequency, Pxx.real[:125], lw=0.8, color='tab:blue')
ax.set(title='Power spectrum of x', xlabel='frequency', ylabel='power')
# パワースペクトルPyyの描画
ax = plt.subplot(224)
ax.plot(frequency, Pyy.real[:125], lw=0.8, color='tab:red')
ax.set(title='Power spectrum of y', xlabel='frequency', ylabel='power')
plt.tight_layout()【実行結果】
理解が追いつかない計算結果と可視化。
魔法を見ているかのようです。
③ クロススペクトルの描画
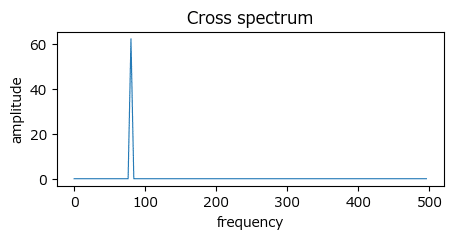
クロススペクトルを算出して描画します。
テキストの図5.9下段に相当します。
### クロススペクトルの描画 ※図5.9下段に相当
# クロススペクトルの算出
Cxy = X.conjugate() * Y / 250
# 描画
fig, ax = plt.subplots(figsize=(5, 2))
ax.plot(frequency, abs(Cxy)[:125], lw=0.8)
ax.set(title='Cross spectrum', xlabel='frequency', ylabel='amplitude')
plt.show()【実行結果】
テキストによると、80Hz付近で$${\theta(80)=\pi/2}$$:90度位相がずれている、そうです。
### 21番目の要素が80Hzでのθです。π/2位相がずれています
# .imagで虚部を取り出しています
np.log(Cxy/abs(Cxy)).imag[20]【実行結果】
Rスクリプトの実行結果と正負が逆になりました。。。
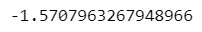
④ コヒーレンスの算出
scipy を用いてパワースペクトル・コヒーレンスを算出します。
コヒーレンスの算出はうまくいきませんでした・・・。
パワースペクトルは periodogram を利用して算出します。
### パワースペクトルの算出 scypy.signalのperiodogram
# 初期値設定
fs = 1000 # サンプリング周波数1000
# 周波数f, パワースペクトルpsの算出
f_x, ps_x = periodogram(x=x, fs=fs, scaling='spectrum', detrend=False)
f_y, ps_y = periodogram(x=y, fs=fs, scaling='spectrum', detrend=False)
# 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 2.5))
ax1.plot(f_x, ps_x, lw=0.8, color='tab:blue')
ax1.set(title='Power Spectrum of x', xlabel='Frequency [Hz]', ylabel=r'$U^2$')
ax2.plot(f_y, ps_y, lw=0.8, color='tab:red')
ax2.set(title='Power Spectrum of y', xlabel='Frequency [Hz]', ylabel=r'$U^2$');【実行結果】
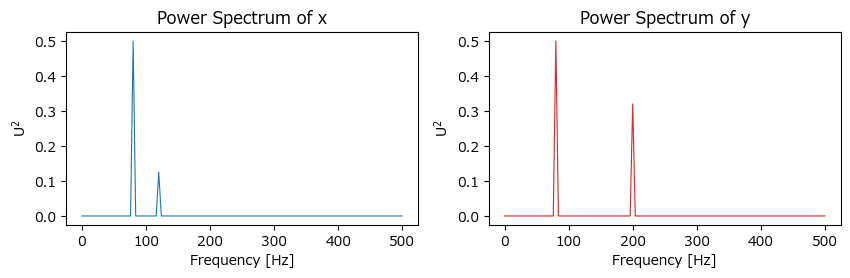
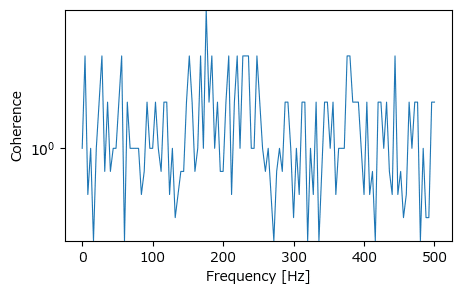
コヒーレンスは coherence を用いて算出します。
たぶん、適切な結果になっていないです。
### コヒーレンスの算出 scypy.coherence ★Rスクリプトの結果と全く異なってる
# コヒーレンスの算出
f_xy, C_xy = coherence(x, y, fs=fs, detrend=False)
# 描画:対数目盛
plt.figure(figsize=(5, 3))
plt.semilogy(f_xy, C_xy, lw=0.8)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Coherence')
plt.show()【実行結果】
Rスクリプトの出力結果のような美しい姿になりませんでした(泣)

ウェーブレットクロススペクトル解析
テキスト「5.4.2 ウェーブレットクロススペクトル解析」のコードを実践します。
こちらも正直なところ、個人的によく分からない領域です。
テキストによると、刻一刻と変化する対人相互作用場面のような「時間経過とともに周波数成分が変化する」場合には、ウェーブレット変換を取り入れたウェーブレットクロススペクトル解析で、周波数領域における時系列データの関係の時間的な変化を見ることができるそうです。
① モルレーウェーブレットの描画
テキストにならって、モルレーウェーブレット関数を作成して描画します。
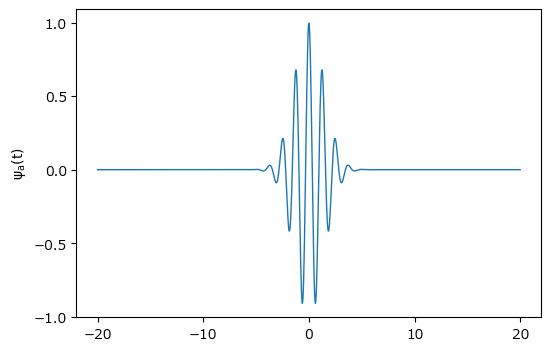
テキストの図5.11に相当します。
### Morletウェーブレットの形状の確認 ※図5.11に相当
# モルレーウェーブレット関数の定義
def morlet(x):
return np.exp(-x**2 / 4) * np.cos(5 * x)
# x軸xとモルレーウェーブレットyの算出
x = np.linspace(-20, 20, 1000)
y = morlet(x)
# 描画
plt.figure(figsize=(6, 4))
plt.plot(x, y, lw=1)
plt.xticks(range(-20, 21, 10))
plt.yticks([-1, -0.5, 0, 0.5, 1])
plt.ylabel(r'$\psi_a(t)$');【実行結果】
0付近でピンと波立つ佇まいが美しいです。
おまけ!
scipy.signalのmorlet関数を用いて描画してみましょう。
### おまけ:morletの描画
plt.plot(signal.morlet(100,1),'blue')
plt.plot(signal.morlet(100,10),'tab:gray')
plt.plot(signal.morlet(100,24),'tab:red');【実行結果】

ここからは、某国の2016年大統領選挙におけるInstagram投稿数の分析に入ります。
② データの読み込みと前処理
RのWaveletCompパッケージのファイル(zipファイル)をWebサイトより読み込み、「USelection2016.Instagram」データセットをPandasのデータフレームに格納します。
まずはWebサイトよりダウンロードしてローカルPCに保存します。
### USelection2016.Instagramファイルのダウンロード
## 設定
# ダウンロードファイルの格納先パス+ファイル名
filename = r'./WaveletComp_1.1.zip'
# zip解凍ファイルの格納先パス+ファイル名
ext_file = r'WaveletComp/data/USelection2016.Instagram.rda'
# ダウンロードの実行
url = r'https://cran.r-project.org/bin/windows/contrib/4.3/WaveletComp_1.1.zip'
res = requests.get(url)
with open(filename, mode='wb') as f:
f.write(res.content)
# zipファイルよりUSelection2016.Instagramファイルを解凍
with zipfile.ZipFile(filename) as zf:
zf.extract(ext_file)続いてPandasのデータフレームに読み込みます。
## USelection2016.Instagram Rdataの読み込み https://pypi.org/project/rdata/
# ファイルの読み込み・解析
parsed = rdata.parser.parse_file(ext_file)
# データの変換:辞書型(中のデータ形式はxarray)
converted = rdata.conversion.convert(parsed)
# データフレーム化
insta_df = pd.DataFrame(converted['USelection2016.Instagram'])
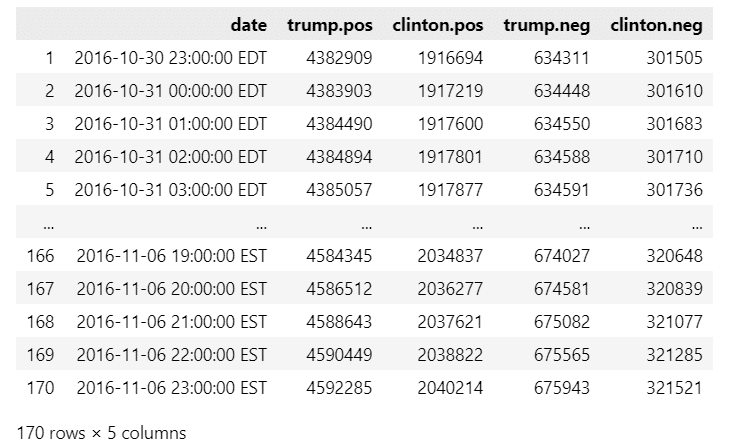
display(insta_df)【実行結果】
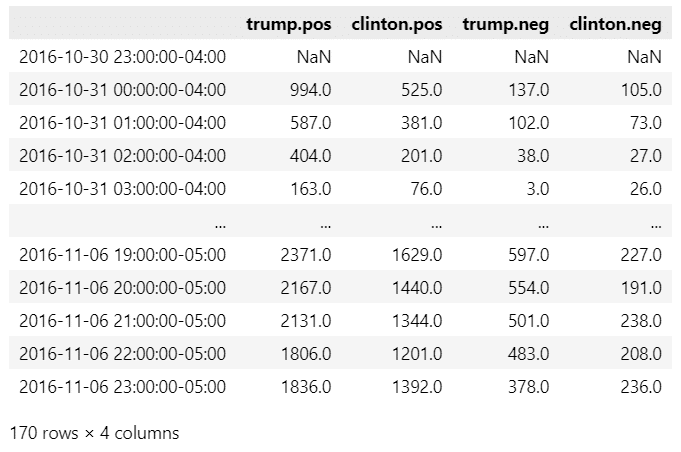
dateが投稿日時(1時間単位)、2人の候補の名前の後ろのposが支持、negが反対を示しています。
値は累計投稿数のようです。
毎時単位の投稿数データを作成します。
### 毎時の投稿数データの作成(時間単位の差分)
posts = insta_df.iloc[:, 1:].diff()
display(posts)【実行結果】
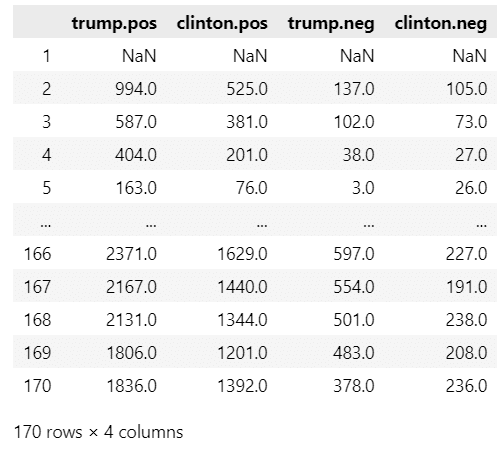
取り扱いデータの途中でサマータイム終了が起きているので、調整します。
### タイムゾーンを考慮したデータフレーム化
# アメリカ東部のタイムゾーンを設定
set_tz = tz.gettz('US/Eastern')
# Rデータセットの日付変換処理
date_idx = pd.date_range(start=datetime(2016, 10, 30, 23, 0, 0, tzinfo=set_tz),
periods=len(insta_df), freq='H')
# 変換後の日付データとpostsデータを結合
df = posts.copy()
df.index = date_idx
# データフレームの表示
display(df)【実行結果】
データが完成しました。
③ 支持投稿数を描画
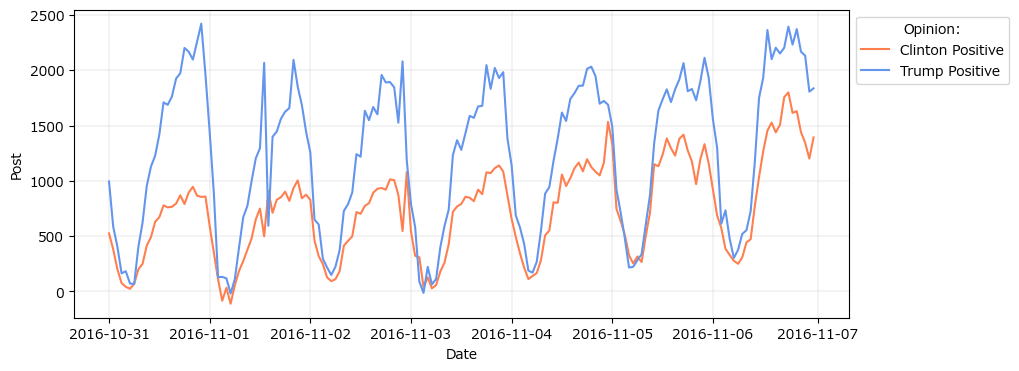
テキストの図5.12に相当する各候補を支持する投稿数のグラフを描画します。
### クリントン支持とトランプ支持のInstagram投稿数の描画 ※図5.12に相当
# 描画領域
plt.figure(figsize=(10, 4))
# クリントンの支持投稿数の描画
plt.plot(df.index, df['clinton.pos'], color='coral', label='Clinton Positive')
# トランプの支持投稿数の描画
plt.plot(df.index, df['trump.pos'], color='cornflowerblue',
label='Trump Positive')
# 修飾
plt.xlabel('Date')
plt.ylabel('Post')
plt.legend(bbox_to_anchor=(1, 1), title='Opinion:')
plt.grid(lw=0.2)
plt.show()【実行結果】
両候補者の支持投稿数は24時間周期を示しているようです。
青い波の候補者の投稿数が圧倒的に多いようです。
④ 支持投稿数をウェーブレット変換してスカログラムを描画
ウェーブレット変換とスカログラムの描画の処理が妥当なのか、かなり不安があります。
scipy.signal の cwt でウェーブレット変換を行います。
引数でウェーブレット関数 signal.morlet2 を適用してみました。
ただし、出力結果のスカログラムの妥当性が分からない状況です。
### トランプ支持者の投稿のウェーブレット変換
## データの設定
# データの標準化
std_trump = (df['trump.pos'] - df['trump.pos'].mean()) / df['trump.pos'].std()
# 幅の設定
widths = np.arange(6, 36)
## ウェーブレット変換の実行 ウェーブレット関数:morlet2
cwtmatrix = signal.cwt(std_trump[1:], signal.morlet2, widths)
## 描画
plt.imshow(abs(cwtmatrix), aspect='auto', cmap='turbo',
extent=[std_trump.index[0], std_trump.index[-1], 30, 0],
)
plt.colorbar()
plt.xticks(rotation=20)
plt.yticks([0, 12, 24])
plt.ylabel('period(hours)')
plt.show()【実行結果】

テキストでは1週間継続する24時あたりの赤い帯が、このグラフでは12~18時のあたりに位置しています。
全体的な色模様の関係は、テキストの24時間に広がる領域が、このグラフではキュッと12時間に詰まっているかのようであり、時間の単位が相違している感じがします。
なんとなくウェーブレット変換がうまく行っていない感じがします。
また、次のグラフである「クロススペクトル、位相差を表す矢印」の計算・描画方法を検討するのに時間がかかりそうです。
変換処理の悪さ、方法検討時間の浪費回避などを理由に、図5.14の作成を断念します。スミマセン。

位相差の評価
Googleの「おはよう」と「おやすみ」の検索数の時間差を位相の観点で分析する節です。
私の限界を超えるテーマになってしまいました。
書いてみたけど妥当性が分からない状態のコードを掲載します。
① データの読み込みと前処理
pytrends を利用して、Googleトレンドの接続、検索数データの取得を行います。
取得結果はpandasのデータフレーム trend に格納します。
なお、「TooManyRequestsError (code 429)」エラーが発生するので、timeframeで指定するデータ取得期間を短くしています。
### Googleトレンドから検索キーワードの検索数を取得
# Googleトレンド接続用の設定
pytrends = TrendReq(hl='ja-JP', tz=540, retries=3)
# 検索キーワードのリストに設定
keywords = ['おはよう', 'おやすみ']
# Googleトレンドに接続
pytrends.build_payload(keywords, timeframe='2023-11-19T15 2023-11-22T15',
geo='JP')
# 検索回数を取得
trend = pytrends.interest_over_time().drop('isPartial', axis=1)
# 取得データの表示
display(trend)【実行結果】
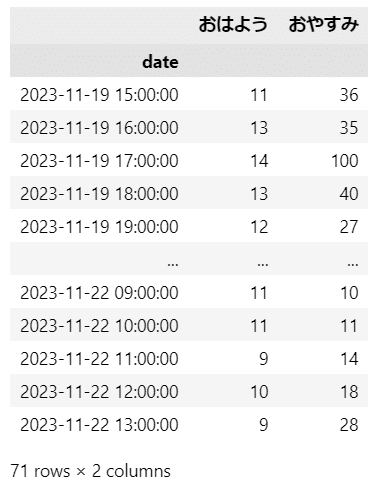
2023年11月19日15時から11月22日13時までの1時間毎の検索数です。
次のグラフ描画で判明しますが、時刻がズレている感じがします。
② グラフ描画
pandasのplotを利用します。
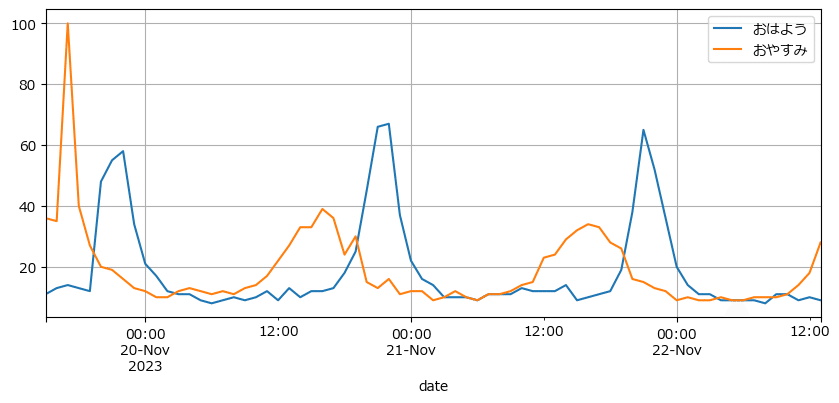
テキストの図5.15に相当します。
### 描画 ※図5.15に相当
trend.plot(figsize=(10, 4), grid=True);【実行結果】
おやすみの頂点の少し後におはようの頂点が表れています。
ただし、15時間くらいズレているようなので、日時の情報をうまく取れてないと思われます。
このまま続けましょう。
③ 位相差の算出とプロット
瞬時位相か位相差の算出がうまく行っていない感じです。
Python にはこんなライブラリがあるんですよ、くらいの気持ちでお読み下さい。
瞬時位相を求める関数は次のサイトのコードを利用させていただきます。
ありがとうございます!
また、円状のグラフは pingouin の plot_circmean を利用しました。
pintouin はメジャーな統計パッケージに実装されていない「かゆいところに手が届く」機能を提供する素敵なパッケージです。
### ヒルベルト変換・瞬時位相の算出とプロット
# ヒルベルト変換と瞬時位相を求める関数
# https://labo-code.com/python/hilbert-transform/
def calc_hilbert(sig):
z = signal.hilbert(sig) # ヒルベルト変換
phase_inst = np.unwrap(np.angle(z)) # 瞬時位相
return z, phase_inst
# ヒルベルト変換、瞬時位相の算出
ohayo_h, ohayo_p = calc_hilbert(trend['おはよう'])
oyasumi_h, oyasumi_p = calc_hilbert(trend['おやすみ'])
# 位相差のプロット ※図5.16に相当(のはず)
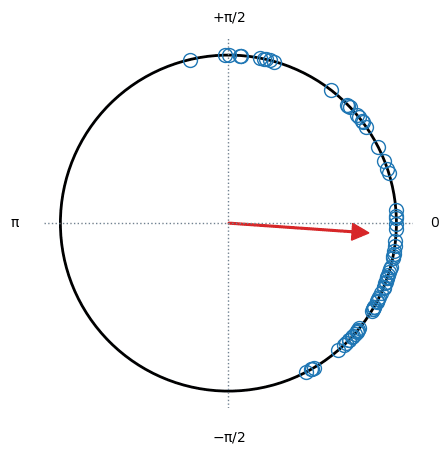
pg.plot_circmean(oyasumi_p - ohayo_p);【実行結果】
円弧上にデータ点をプロットできました!
矢印は「vector length of a set of angles in the unit circle」(単位円の角度のベクトル長さ?)です(pingouin の plot_circmean のサイトより)。
しかし結果は、テキストと比べて時計回りに90度ほどずれてしまいました(泣)
いくつかのRコードの対応は見送ろうと思います。

イベント周期の安定性
24時間の時刻のように循環するデータの平均は、合計の単純平均では不正確であり、円のような循環・周期を考慮して平均を求める必要がありそうです。
テキストでは時刻を角度と考えて方向統計学の考え方を適用するとしています。
ここでは、テキストの仮想就寝時刻データについて、方向統計学による平均値を求めて、平均値に関する統計的仮説検定を実施します。
pingouin パッケージのおかげで、適切そうな結果になりました。
① データの作成
### データの作成:就寝時刻
time = np.array([23.5, 0, 22.75, 23.5, 0.5, 1.5, 2, 23.25, 1, 23])
print('就寝時刻:', time)【実行結果】

② ラジアンの計算
テキストの計算方式と pingouin の convert_angles の方法で計算してみます。
### 時刻を方向データに変換:単位はラジアン
# テキストの計算方式
radian_val = time / 24 * 2 * np.pi
print('ラジアン:', radian_val.round(3))
# pingouinで時刻をラジアンに変換
print('pingouin:', pg.convert_angles(time, low=0, high=24, positive=True).round(3))【実行結果】
0時「0」から23時59分…「$${2\pi=6.28 \cdots}$$」に変換されました。

③ ラジアン(方向データ)の平均値の計算
pingouin の circ_mean() を利用します。
### 方向データの平均値を算出 pingouinのcirc_meanを利用
ave_rad = pg.circ_mean(radian_val)
print(f'就寝は平均 {ave_rad / (2 * np.pi) * 24:2.1f} 時')【実行結果】
テキストと同じです~(ホッ…)

④ レイリー検定
就寝時刻が完全にランダムなのか、特定の時間帯に偏っているかをレイリー検定で確認します。
テキストによると、レイリー検定の帰無仮説は「タイミングは一様に分布している」です。
pingouin の circ_rayleigh を利用します。
### レイリー検定:帰無仮説「母集団は円の周りに一様に分布している」
# pingouinのcirc_rayleighを利用
z, pval = pg.circ_rayleigh(radian_val)
print(f'レイリー検定: [z値={z:.4f}, p値={pval:.3f}]')【実行結果】
p値が0.000であり、帰無仮説は棄却できます。
したがって、就寝時刻は特定の時刻に偏っていると言えます。
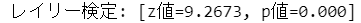
以上で終了です。
お疲れ様でした。

第5章 その3 へ続く
■次回の取り組みテーマ
・時系列クラスタリング
・再定量化分析
・グレンジャー因果性検定とVARモデル
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
