
感情の起伏を関数したい
数学と感情
「数学は無機質だ」「数理モデルは人間の行動や感情を予測するのには疎い」等言われておりますが、実際、感情の起伏の分析に数学が入り得る余地はあるのでしょうか。今回は、「感情の起伏」を簡単な関数なりで表すことが可能か。多分不可能だと思うので、その試みをする際に考えるべきポイントを私なりにピックアップしていきたいと思います。
感情の関数
人の感情に関する性質を表す際よく用いられるのが、「感情が乏しい人」や「感情の起伏が激しい人」「感情表現が豊かな人」等でしょうか。
ですが例えば、「感情の起伏が激しい人」と表現する際、具体的には、どのような性質を喩しているのでしょうか。「起伏」とは「高くなったり低くなったり」「盛んになったり衰えたり」「変化があること」として、
(1)感情の変化の幅が激しい。(例えば、感動する映画を見て号泣し、高得点のテストの結果に対し両手上げてジャンプして喜ぶタイプ)
(2)感情の変化の頻度が多い。(例えば、さっきまでケーキ食べて満面の笑みだったのに、カフェからの帰り際に雨が降り始めたのを見ただけで、かなり膨れっ面になるタイプ)等でしょうか。
これを数学的に考えるとして、まず、問題になるのが
考えるポイント1: 感情は"Linear" (直線)か "Non-linear" (非直線)か言い換えるならば、私たちの感情は、何かの事柄に対して一直線の感情を抱くことがあるかです。
今回、矢印や座標に数値を入れていないのですが、とても簡単に感情をY、時間の経過をXと想定しています。(*今回すべてのグラフを全部 x∈[-5,5]でざっくり計算して作ってしまいました。)

「バンドの追っかけを生き甲斐にしている人の月末に来るべきライブに対する感情の高まり」はどうでしょうか。例えば、彼または、彼女の生活や意識において、バンドが80%のウェイトを閉めるならば、時間の経過(この場合ライブ当日との時間的距離感の推移)により一直線に近い気持ちの変化があるのかもしれないです。
しかし、ぴったり一直線ではない気がします。例えば、ちょうど一週間前の土曜日の夜の方が、直前の水曜日よりライブに対する現実感が増し、気持ちの高揚感が高いかもしれないですね。
非直線の感情
では、非直線だったらどうでしょうか。非直線と言っても、色々なサンプルタイプがあります。
例えば、


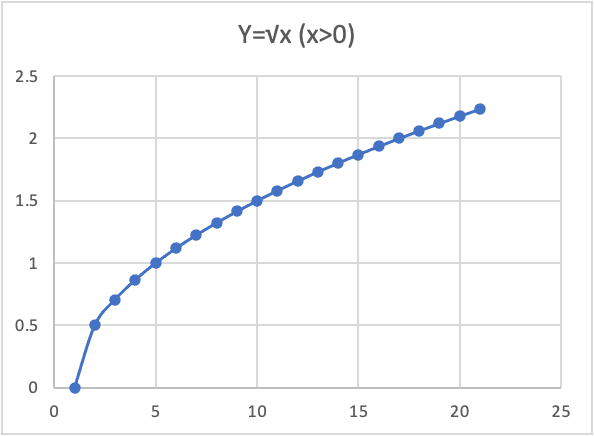



ここで考えるべきは、
考えるポイント2: 感情の加速度はどの程度か
数学的にはsecond-order derivative がどんな感じかです。
ライブが近くにつれ気持ちの盛り上がりが加速するのか。逆に、ライブが近くにつれ、その現実味が増し、ある程度高揚感が抑えられていくのか。
考えるポイント3: 点の頻度はどの程度か。
今回 Discrete Time (離散型時間)といって個々の独立した観測点を有する感じで表現してみましたが、Contious Time (連続時間)といってすべての観測値が連続しているかのように捉える感じの方が、よいのでしょうか。
考えるポイント4: そもそも、私たちの感情において観測点とは、具体的に何を示しているのでしょうか。感情の観測点=「私たちが自分の感情を意識する瞬間」という解釈はどうでしょうか。だとしたら、私たちは、自分の感情を連続して意識しているのか、あるいは、ある地点ごと、何かを契機に意識しているのでしょうか。
例えば、今日私が起きてから、大小様々な感情を意識しましたが、8時間連続で何かしらの感情を意識している気はしなかったです。今も、ほぼ無意識に何となく自分の現在進行の思考を垂れ流しタイピングしているので、あまり強い感情は感じていないです。
感情の波
感情に「波」があると表現するよう、SinやCosで表してもいいのかもしれないです。さらに、長期的な「人生山あり谷あり」とは、これまさにこれらSin Cos の特徴ですね。
これは女性の気分に影響を与える月のホルモンの分泌量のグラフにもちょっと似ているのでしょうか。

考えるポイント5 : 感情のベクトル、感情に向きはあるか
考えるポイント6: そもそも、感情は常に意識的なものなのでしょうか、無意識になり得ないのでしょうか。?「感情」と言っているのだから、「感じている」つまり、意識しているでしょうか
感情には強弱があるとして、よりその強弱を線の濃さや三次元目で表したいところです。
以上のグラフは、すべて感情をY、感情に影響を及ぼす要因をXとして二次元(Y,X座標)で作ってみましたが、実際には、要因は1つ以上あるはず、つまり、「多次元な感情」であるため、回帰分析なり、ソフトウェアを使った多次元モデリングによりより具体化しそうです。
感情の回帰分析
また、回帰分析を使って、来月の自分の感情の起伏を予測するのもとても興味深いです。
例えば、
私の感情に影響を及ぼす要因は何なのか。少し考えてみたところ、さっとこの辺りかなと思いました。

y=感情の予測値
感情に影響を与える変数
Beta1=体調(睡眠、栄養、ホルモンサイクル)
Bata2= 仕事・勉強(テスト、資格受験日、昇進日、大事なプレゼン、企画したイベント当日)
Beta3= 金銭(支払日、給料日)
Beta3=プライベートな予定
Residual =予期しない出来事に対する余地
ここで、問うべきなのが、
考えるポイント7: 分析の目的が「過去の感情の分析」なのか「感情の予測」なのか
考えるポイント8: もし後者だった場合、過去のデータを元に未来を予測するか。過去のデータから学ぶか (ML等)。実際過去の感情パターンをを私たちはどれほど繰り返していくのだろうか。
感情に関する失敗を学ぶ。感情のコントロールが上手くなる。感情のフィードバック。感情は前に進むのか、滞るのか。
考えるポイント8: どっちから始めるか。データか、仮定か
感情の最適化
このあたりで登場するのが、経済学の十八番である最適化問題ですね。そもそも、
考えるポイント9: 私たちは感情は最適化すべきか、安定化すべきか
私たちは、感情を最適解を求める必要があるのでしょうか。はたまた、安定した感情を持つべきなのでしょうか。例えば、感情の起伏が激しい方や闇落ちしやすい方は、感情を一定レベル以上に維持することで、QOLが急上昇するかもしれないです。また、躁鬱の気味の方は、感情の下限だけでなく上限もコントロールできたらと考えるのかもしれないです。
しかし、
考えるポイント10: 最適化すべきは、短期的な感情か長期的な感情か
長期的な感情。例えば、文化、生物学的性別と性別、社会的慣習、社会的役割が様々な感情の起伏の根底にありそうです。一方、短期的な感情としては、「瞬間的な出来事」により誘因されるものでしょうか。
考えるポイント11: 私の感情は他者の感情から影響を受けるのか。それともある程度独立しているのか
共感性羞恥心、HSPなど他者の感情との交わりが最近話題になっているよう私たちの感情は内側に対し複合的になっているだけでなく外側に対しても複合的に作用しているはずです。
例えば、「彼女が幸せそうなら、私も幸せ」「おつぼねさんの感情が落ち着いていれば職場が平和で私の心も安定する」など自分以外の他者の感情に依存している、影響されている場合も多々あると思います。その場合は、自分の感情だけではなく、それらの感情の分析も必要になってきます。
これまで、個人単位での感情の変化を検討してきましたが、「多数の感情の変化」を私たちは捉えて予測することができるでしょうか。
考えるポイント12: 感情の総和?「多数の人々の感情の平均値」は意味をなすのか。
雨の日は「多数の人々の感情の平均値」が晴れの日より低くなるのではないでしょうか。クリスマスや年末年始の祝日はどうでしょうか。
さらに言うならば、人々の感情の変化と景気に関係性はあるのでしょうか。因果関係はどうでしょうか。
まとめ
考えるべきポイント沢山ありそうです。感情研究は分野的には、心理学、神経学等でしょうか。とても楽しそう🐰ワクワクしてきました
