
【ベクトル】 〈3〉 内分点・外分点
ベクトルは、小学校からずっと習ってきた「数」とは、ちょっと異なる「量」です。方向が加わっているのが理由ですが、そのおかげで「図形」にも応用しやすく大変便利な道具です。
「数」+「図形」、つまり、長さや成分のような数量=代数的な意味合いと、方向を持った矢印=幾何的な意味合いが含まれているのがベクトルです。「方程式」の解説でも述べましたが、数学の面白さ、美しさを味わうことのできる分野ですので、順に、整理していきましょう。
[Method] 内分点の公式

① 図形と方程式、ベクトルの成分表示

② 位置ベクトル

③ 始点の付いたベクトル(平面・空間)

覚えやすいのは②「位置ベクトル」
基本的に、すべて①の公式と同じなのですが、実は一番覚えやすいのは、②だと思います。一番シンプルで、文字も少ないので。
「位置ベクトル」はイメージしにくいかもしれませんが、頑張って②をマスターすると、①③の理解も深まると思いますよ。
求めようとする点もすべて位置ベクトルとするタイプなので、割りきって、位置ベクトル=座標のようなもの と考えてみましょう。
〈例題1〉「位置ベクトル」

〈例題解答例1〉

多用するのが、③「始点の付いたベクトル」の形です。
始点があるので、図形上で幾何的に扱おうとすると、すごく難しいと思います。始点をあまり考慮せず、終点だけに着目して、公式通り代数的に処理するとスピードと確実性があがるように思います。

〈例題2〉「始点の付いたベクトル」
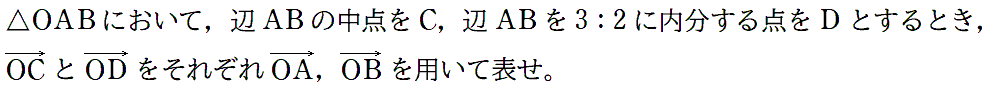
〈例題解答例2〉

上記例題2において、例えば中点Cは、一旦、OA→+OB→ を図形的に考えて、さらにその半分として求めることもできます。しかし、点Dになると図形的に求めるのは、かなりたいへんです。
つまり、内分、外分では、公式を使って代数的に求めていくほうが、脳の消耗が少なくて済むのです。

[Method] 幾何的←→代数的
どちらに主眼を置いて処理するのかの匙加減がベクトルの難しいところ
だと思います。
ただし、この匙加減がわかってくると得意分野にできるのが「ベクトル」です!
〈例題3〉

〈例題解答例3〉

[Method] 外分点の公式


外分が出題された場合、いつも平均点が低くなります。みんな、苦手ということですね。まずは、A、Bのどちらの延長線上にあるかを図示してみることが肝要です。「位置ベクトル」を求めるのは、m、nのどちらかをマイナスにして扱います。
かけあわせるのは、以下のMethodを使ってください。
[Method]
mは、AとQを結んでいるので、結ばれていないBとかけます。
nは、BとQを結んでいるので、結ばれていないAとかけます。
これは、内分の場合も同様です。
〈例題4〉

〈例題解答例4〉

〈問題5〉

〈問題解答例5〉

〈問題6〉

〈問題解答例6〉

〈問題7〉

〈問題解答例7〉

