
【微積分】 〈14〉 放物線✖️2接線(a/12公式)
図形によって、囲まれる部分の面積の求め方は様々です。「代数と幾何の一対一対応の美しさ」という観点から観ると、代数的な「関数」から、幾何的な「面積」が求まる「積分」は、まさにその典型です。
このシリーズでは、複雑な計算になりがちな「積分」について、スピードと確実性のアップを目指して解説します。
この種の公式は、領域(面積)を構成する要素(放物線、直線、接線、交点など)によって違うので、グラフを描いて、イメージをしっかり持って、適切に扱えるようにしましょう。
練習しているときとテスト本番で大きく違うのは、時間的な制約です。時間が限られると焦りもうまれます。ですから、「練習ではできるのに本番でできない!」ということも起こってしまいます。時間と集中力コストを抑えて、実力を出し切りたいものです。難しいけどね。
今回は、ちょっとマイナーではありますが、高効率公式です。以下のグラフの斜線部分のような複雑な形の面積が求まります。まともに計算しようとすると、接線の交点の左右で2カ所の積分が必要です。計算も大変だし、時間もかかるし、集中力も使ってしまいますよね。この高効率公式を使ってみてはいかがでしょう。
ただ、面積と接線の交点のx座標はわかるのですが、接線の方程式を直接求めることはできません。そこは注意点ですね。
[Method] 放物線✖️2接線=「1/12公式」=「a/12公式」


[Method] 2接線の交点
2本の接線の交点のx座標は、2つの接点のちょうど真ん中で

この公式も前回、前々回と同様に、2次の係数 a を落とさないように注意しましょう。
以下の例題では、まず、普通に計算して求めていますが、それでも、積分公式の応用(正確には数学Ⅲの領域)を用いています。
高効率公式を用いると、途中計算が省略されて、答えがすぐに求まるような記述になります。
<注意> 数学Ⅲの範囲ですが、使ってもよいと思われます。

例)xの係数は1でないといけないので注意!

〈例題1〉
〈例題解答例1〉

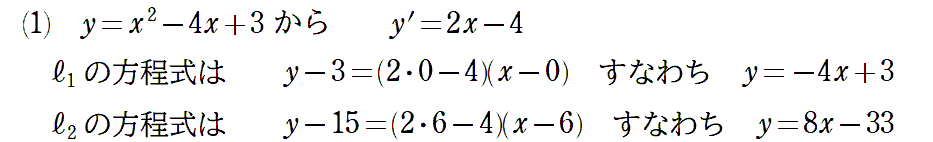


〈問題2〉

〈問題解答例2〉


〈問題3〉

〈問題解答例3〉


〈問題4〉

〈問題解答例4〉


