
【方程式】 〈2〉 2次方程式
数学では、2次方程式、円の方程式、ベクトル方程式など、様々な「方程式」が登場しますよね。しかし、実は、違う意味合いの3種類が混在しているのです!
高校数学のレベルで、きちんと整理・解説していきますので、「そうだったのか!」「Methodを理解!」という領域まで到達していきましょう。
「方程式」は3種類
高校数学の範囲で学習する上程式は、大きく分けて3種類あります。
1⃣ 未知数を求める=解く(2次方程式、3次方程式など)
2⃣ 図形を表す(直線の方程式、円の方程式、ベクトル方程式など)
3⃣ 関数を求める(積分を含んだ式、微分方程式など)
1⃣ 解く (ⅰ) 2次方程式
一番一般的な形で、わからない文字 x の値を求めるのがこの種の方程式です。ただxの次数によって、解法がぜんぜん違ってきます。数学の不思議ってこんなところにもあります。アーベル・ルフィニの定理は、5次以上の方程式には解の公式が存在しない、と主張しています。
2次方程式は、方程式の次数と解の個数の関係、解と係数の関係、関数とのかかわりなど、様々な側面で、方程式の学習の基礎と言えるでしょう。
まずは、「方程式を解く」ことからはじめ、解についても多面的に考えていくことにしましょう。
[解法1] 因数分解

(数学的・学問的ではないけれど、)特に入試の側面から言って、因数分解を使った解法は、以下の3点で、優れた解法と言えるでしょう。
① 速度が速い
② 正確性が高い
③ ミスを見つけ易い


展開してしまう人もいるんじゃないかな?
展開すると、速度が遅くなり、計算間違いの確率も上がります。
できるだけバラバラにしないように心がけましょう。

なお、4次方程式の解法のうちで、複 2 次式(次数がすべて偶数の項のみからな る多項式)では、この因数分解に帰着します。
[解法2] 解の公式
因数分解ができなければ、やむを得ず解の公式です。
(5) のように、ルートが係数にある場合は、ほぼ因数分解です。


[Method] 方程式から片側変形式へ
もちろん、問題は、左辺=右辺 の方程式の形をしています。
ところが、解の公式による変形に入った瞬間に、
x=…=… となって、片側変形式になります。分母を払うような計算はできないので、勘違いしないように注意しましょう。
ここにも“つまずき“ポイントがあるように感じています!
[Method] 解の公式とは =グラフとの連関

解の公式は、中学校の最後に学習するので、習熟が進んでいない人もいるように思いますが、侮るなかれ、実は、解の公式は、2次関数と深い関連があるのです。
簡単に触れておくと、以下の2次関数について、そのグラフは、

解の公式を以下のように変形し、見方を変えてみると、
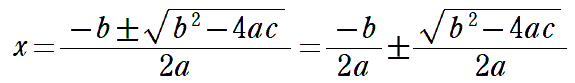
前半部分(-b/2a)は、グラフの軸の位置を表している。後半部分(√~/2a)は、軸(-b/2a)の値に足したり、引いたりするのだから、x軸上で、軸からα、βへ、左右に開く距離を表している。
詳しくは、解とグラフの関係を解説するシリーズで。
〈練習1〉

〈解答例1〉


