【#38】材料力学の強化書 〜ひずみエネルギー（１）〜

今回のトップ画像は、兵庫県は神戸にあるフロインドリーブと呼ばれるカフェの内装です。教会をリノベーションしたそうで、そうそこら辺のカフェでは見られない雰囲気が味わえそうです。

さて、材料力学の話に戻りましょう。

前回は数学の復習として、行列の固有値問題について説明しました。高校数学で習う行列を物理で利用することについては、初見の方も多かったかもしれません。

今回は弾性変形におけるエネルギーの扱い方を説明します。高校物理で習うばねのエネルギーと類似の関係が弾性体のひずみエネルギーでも成立します。ここは高校物理の内容を思い出して頂きながら、話を進めたいと思います。

ひずみエネルギーの定義

物体が外力の作用によって変形した場合、外力は物体に仕事をします。このとき、物体の運動を無視できるときは、外力のなした仕事量に相当するエネルギーが物体に蓄えられます。このエネルギーのことを「ひずみエネルギー」と言います。

特に、変形が弾性変形である場合、外力を取り除けば物体は元の形に戻り、ひずみエネルギーは外部に解放されます。このような可逆的なひずみエネルギーを「弾性ひずみエネルギー」と言います。

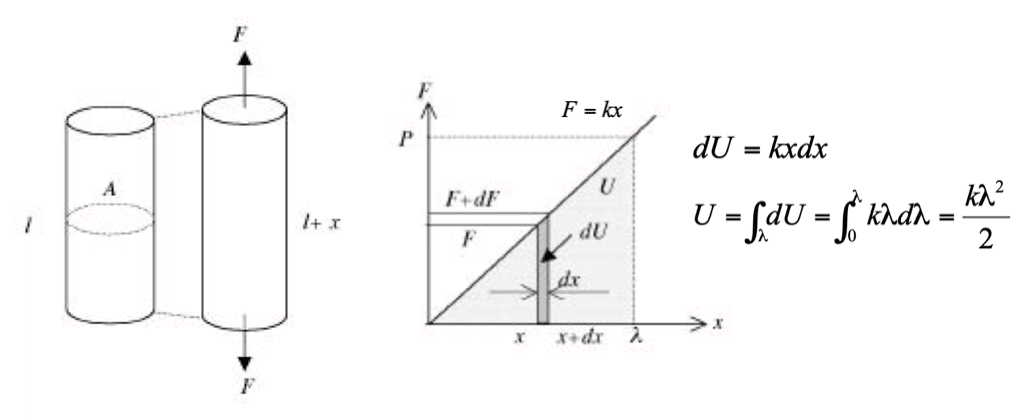
例えば、バネのひずみエネルギーを考えると、次のようになります。フックの法則から外力を変位（ｘ）の関数として導き、変数（ｘ）で積分することで、バネに蓄えられるひずみエネルギーを計算します。

物体に蓄えられるひずみエネルギーは、次の２通りの方法で求めます。

■外力のなす仕事から求める方法
物体全体の系を考えて、外力のなす仕事から物体に蓄えられるひずみエネルギーを求めます。

■内力のなす仕事から求める方法
物体内部の微小部分の系を考えて、系に作用する内力のなす仕事（微小部分に蓄えられるひずみエネルギー）を求めます。これを全体に積分します。

先ほどのバネに蓄えられるひずみエネルギーの計算については、前者の方法を適用しました。

軸力を受ける棒のひずみエネルギー

一様な断面積を持つ長さ（ｌ）の棒に外力が付与した状態を考えます。先ほど紹介した「外力」と「内力」のなす仕事からひずみエネルギーを求めてみます。

外力（Ｆ）はフックの法則から変位（ｘ）に比例するので、最終的な外力（荷重）をＰとしたとき、フックの法則から、

$${P=k\lambda}$$

のように書くことができます。そして、外力のなす仕事Ｕは変位（ｘ）の関数で表した外力Ｆをｘで積分すれば良いです（積分範囲はゼロから最終的な変位まで）。先ほどの関係を踏まえて、外力のなす仕事Ｕは次のように求められます。

$${U=\frac{1}{2}P\lambda}$$

このＵがひずみエネルギーに等しくなります。

次に、内力のなす仕事からひずみエネルギーを求めてみます。棒の内部の微小部分において、内力Ｎにより微小な伸びが生じているとします。

$${dU_e=\frac{1}{2}Nd\lambda}$$

 ここで、棒の微小部分のひずみ（ε）を定義すると、

$${\epsilon=\frac{d\lambda}{dx}}$$

となります。内力Ｎは荷重（Ｐ）に等しいので、

$${dU_e=\frac{1}{2}P\epsilon{dx}}$$

となります。これを棒の全長（ｌ）まで積分します。

$${U_e=\frac{1}{2}\int^l_0 P\epsilon{dx}=\frac{1}{2}P\epsilon{l}=\frac{1}{2}P\lambda}$$

以上より、外力のなす仕事と内力のなす仕事が一致することが分かり、いずれもひずみエネルギーに等しいことが言えます。

ひずみエネルギー密度

棒のヤング率をＥとすると、先ほど求めたひずみエネルギーは次のように変形できます。

$${U=\frac{1}{2}P\lambda=\frac{P^2l}{2EA}}$$

垂直応力（σ）を定義すると、

$${U=\frac{{\sigma}^2}{2E}Al=\frac{\sigma\epsilon}{2}Al=\frac{E{\epsilon}^2}{2}Al}$$

と書くこともできます。ここで、棒の体積（Ｖ＝Ａｌ）から、

$${U_u=\frac{U}{V}=\frac{{\sigma}^2}{2E}=\frac{E{\epsilon}^2}{2}}$$

と書くことができます。これは単位堆積当たりに蓄えられるひずみエネルギーを表していて、特に「ひずみエネルギー密度」と呼ばれます。

おわりに

今回はひずみエネルギーの扱い方について、簡単な軸力を受ける棒を例題として説明しました。

エネルギーについては、私の仕事でもよく扱う物理量ですので、個人的な復習にもなりましたが、何かと使う機会は多くあるので、ぜひ理解しておいて頂けたらと思います。

次回はねじり・曲げにおけるひずみエネルギーを説明します。

-------------------------

最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに添えるように頑張ります。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎