塑性変形と転位の研究に身を捧げた学生時代の話 -2-

2023年7月23日 15:41

本記事は2022年9月に書いた「学生時代の研究活動」の話の再整理です。

学生時代はとにかく研究に明け暮れた時期でした。実際は塾講師のアルバイトと両立しながらでしたが、キツい時期を乗り越えた感覚があります。ここでの経験が今の仕事のキッカケにもなりました。

私の研究の経歴はかなり特殊です。木更津高専（通常課程と専攻科課程）と筑波大学（大学院）、合わせて６年間の時間を研究活動に注ぎ込みました。

高専と大学院では研究テーマこそ異なりますが、取り組んだ研究の大筋のテーマとしては「塑性変形を数値解析技術を利用して詳細に理解すること」でした。

今回は学生時代の研究活動の軌跡に関して、専門知識も交えながら、数回に分けて書いていくことにします。

前回は主要なキーワードの「塑性変形」と「転位」の意味などの基本事項の話を書かせて頂きました。

今回は主に高専生の頃に取り組んでいた研究活動の話です。研究テーマは「降伏点現象に起因する不均一変形の有限要素法による解析」です。塑性変形の物理に特化した、数値解析（シミュレーション）の走り出しでもありました。

降伏点現象のモデル化

研究はタイトル自体は端的な言い方が多いので、専門用語がどうしても登場しがちです。今回で言えば「降伏点現象」や「有限要素法」など。

ここでは「降伏点現象」から説明します。材料の特性を判断する際に使われる「応力ーひずみ線図」が最も分かりやすいのですが、軟鋼をはじめとした、炭素を一定量含んだ炭素鋼には特有の変形の過程が存在することが知られています。

・上降伏点から下降伏点の応力降下
・一定応力を伴う塑性変形の進行（降伏棚）

巨視的（マクロ）な視点で変形を論じると、応力ーひずみ線図で言うところの上降伏点から下降伏点の応力降下のタイミングこそ、弾性変形から塑性変形に転じる瞬間と言えます。

本研究では、応力降下とその後の降伏棚を合わせて、炭素鋼の特有の「降伏点現象」と定義しています。この現象を論理背景から数式的に表した構成式（応力とひずみの関係を簡潔に表した方程式）は少なくて、本研究では新たに「Hahnの構成式」に注目しました。

参考論文：材料の高速変形と構成式
https://www.jstage.jst.go.jp/article/materia1962/29/5/29_5_337/_pdf/-char/ja

上記の構成式を構造解析のスタンダードと言える「有限要素法」のアルゴリズムに組み込んで、定量的な観点から評価すること。これが本研究の目的になります。

FEM（Finite Element Method）と言います。現在の企業でもお世話になる数値解析技術ですが、この機会に初めて出会いました。

有限要素法：微分方程式を近似的に解くための数値解析手法。解析対象を微小な構成要素で分割して、各要素の条件を連立方程式で近似します。連立方程式を解くことで各要素の数値解が求まり、最終的に全体の挙動を確認します。

工業分野では単位系を考慮した「物理量」を定量的に求めることで、物理現象を数値で把握するために利用されます。製品設計の場面では、往々に事前検討と称して使われることが多いです。

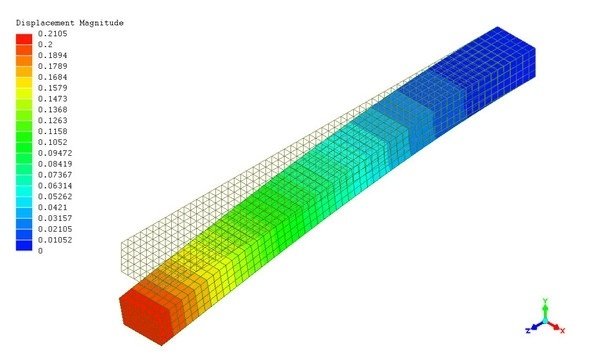
有限要素法はあくまで計算手法なので、簡単なモデルの場合は手計算で対処できます（大学院の時に実際に経験しました）。現実の製品形状をモデルとする場合は、アルゴリズムはもとより、計算処理はコンピューターに任せることになります。

この有限要素法のアルゴリズムに対して、Hahnの構成式を導入することになるのです。

Hahnの構成式の主張は何なのか。理論背景として、ここで紹介しておくことにします。

塑性変形の初期段階とは、金属（炭素鋼）の原子配列がずれること（すべり）が発生すること。これは降伏点現象における「応力降下」の部分に対応します。

ここから「転位」が徐々に発生していき、塑性変形が進行するのですが、Hahnの構成式は転位の増殖過程を新たに考慮した構成式と言えます。

Hahnの構成式の視点にはもうひとつ、転位の飽和という現象があります。塑性変形における「硬化」と呼ばれる現象です。

転位は原子配列のすべりに伴い運動しますが、他の転位や結晶粒界（金属内部の結晶同士の境目）にぶつかることで、運動が止まることがあります。結果的に、結晶粒界で転位が凝集するような様相になります。

硬化は全般的な金属材料に見られる現象です。転位という観点で見れば、転位が飽和状態になることで、塑性変形が進行しにくい状態になる。これが硬化という現象の捉え方になります。

Hahnの構成式を取り込んだ有限要素法を提案することが本研究の目的です。これは微視的（ミクロ）な物理現象をベースとした考え方とも言えます。

高専で取り組んでいた研究の概要を紹介しました。今回は研究内容の説明に留めましたが、次回は実際にどんな研究成果まで漕ぎ着けたのかを話します。

有限要素法との初めての出会いでしたが、この経験を踏まえて現在に仕事に就けたのは、非常に大きいものでした。有限要素法のプログラムを理解するのには大変苦労しましたが、今となっては良い思い出です。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎

#物理がすき

1,557件