【#19】材料力学の強化書 〜断面二次モーメントと断面係数〜

今回のトップ画像は京都の鴨川に架かる橋です。橋の設計は建物とはまた性質が違いますが、安全に人が通れるように設計しなくてはいけませんので、また違う難しさがあると思います。

さて、材料力学の話に戻りましょう。

前回ははりの曲げに対するせん断応力の発生について見ていきました。一般的に曲げには、曲げ応力（垂直方向の応力成分）とせん断応力の両方が含まれると説明しました。

今回は曲げ変形の計算において欠かせない、断面係数について説明します。基本的に断面係数ははりの断面形状によって決まりますが、物理的にどういう意味があるのか、きちんと見ていただけたらと思います。

断面二次モーメントについて

部材の曲げにくさ（曲げる力に対する抵抗性）を知ることは、機械や建築物の設計において大事な指標です。これは主に次の２つで決まります。

・ヤング率：材料固有の固さ
・断面二次モーメント：断面形状で決まる固さ

例えば、材質の観点で見ると、ゴムよりも木材の方が曲げにくいです。これはゴムより木材の方がヤング率が大きいことが理由です。

一方で、断面形状の観点で見ると、正方形とＨ形では曲げに対する固さが変わります。はりの構造ではＨ鋼と呼ばれる部材が使われますが、これは同じ質量に対して正方形よりＨ形の方が断面二次モーメントが大きいことが理由です。

単純な形状の断面二次モーメントを例示します。

また、ネット上に断面二次モーメントの計算ツールがあります。気になる方は調べてみてください。

https://d-engineer.com/unit_formula/sec_moment.html

断面二次モーメントに関しては、一般的な材料力学の書籍では付録として付いていることが多いので、そちらを参考にするでも良いでしょう。

断面係数について

断面係数は言うなれば「部材の断面性能を表す値」のことです。曲げモーメントに対する抵抗力とも言い換えられます。

曲げ応力（σx）は曲げモーメント（M）を用いて次のように表されます。

$${{\sigma}_x={\frac{M}{I_z}}y}$$

この式から、曲げ応力の最大値は中立面から最も遠い面である、はりの上面または下面の位置になることが分かります。はりの上下面までの距離をｈとして、断面二次モーメントをｈで除算した値のことを「断面係数」と呼びます。

これを用いると、はりの上下面での曲げ応力は次の通りになります。

$${{\sigma}_{x1}=-\frac{M}{Z_1}}$$ , $${{\sigma}_{x2}=\frac{M}{Z_2}}$$

最大曲げ応力は上記の２つのうち絶対値の大きい方をとります。言い換えれば、断面係数の小さい面に最大曲げ応力が生じます。

断面二次モーメントの計算例

実際に長方形断面における断面二次モーメントと断面係数を求めてみます。

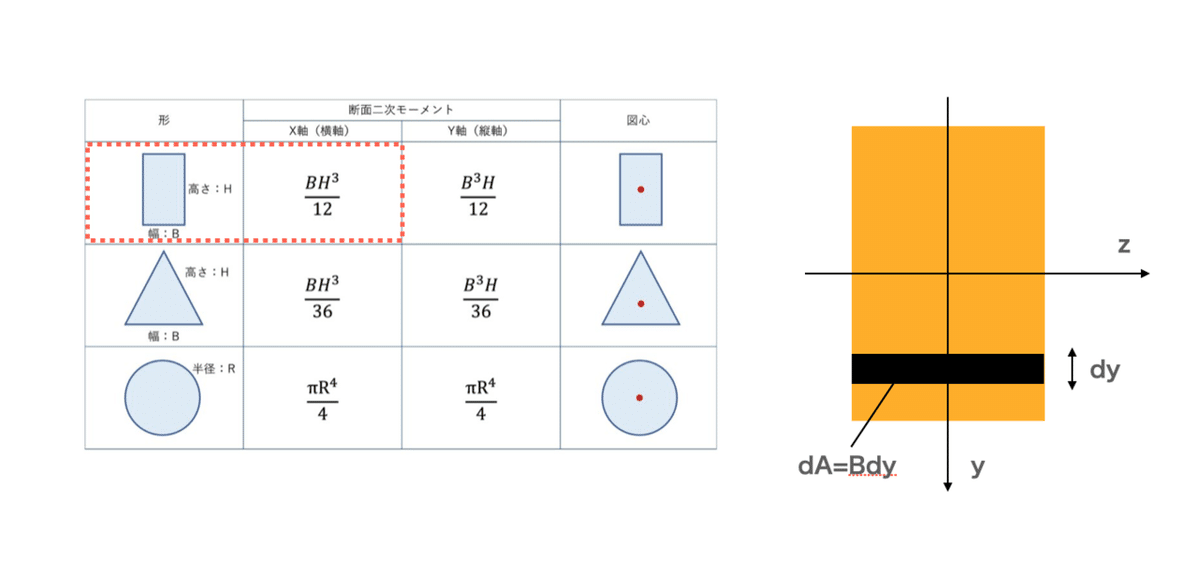
まず、断面二次モーメントの定義式は以前に示していますが、下記の通りでした。

$${I_z=\int {y^2}dA}$$

長手方向をｘ軸で中立面の横方向をｚ軸とします。黒色で示した微小面積の関数を定義式に代入して、ｙ軸に沿って積分します。

$${I_z=\int_{-\frac{H}{2}}^{\frac{H}{2}} B{y^2}dy=2B\int_0^{\frac{H}{2}} {y^2}dy={\frac{1}{12}}BH^3}$$

上記の通り断面二次モーメントを求めたら、断面係数を求めます。先に挙げた断面係数の定義式より、次のように求まります。

$${Z={I_z}/(H/2)={\frac{1}{6}}BH^2}$$

その他の形状に関しても、余力のある方は実際に導出してみると良いでしょう。

おわりに

今回は断面二次モーメントと断面係数について説明しました。

曲げにくさ（曲げる力に対する抵抗性）を知る上で、断面形状は欠かせない要素であることがお分かり頂けたかと思います。

実際に構造物を造る現場でＨ鋼が使われる理由も、断面係数から来ています。この辺は肌感覚もあるかもしれませんが、その理由をきちんと知ることで、材料力学の面白さに火がついてくれることを期待します。

-------------------------

最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに添えるように頑張ります。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎