材料力学から始まる変形理論 -4-

材料力学を起点とした変形理論に関する連載記事。物理的な「変形」にまつわる理論を深掘りします。

前回は材料の変形の特性を理解するために重要な「材料試験」について、特に鉄鋼材料の変形に関する特徴を一例として見てみました。

以前に変形の全ては引張・圧縮・せん断・曲げ・ねじりに集約されると説明しました。引張・圧縮・せん断はこの中でも単純な変形とされていますが、曲げやねじりは少し複雑です。

今回は曲げやねじりの変形について、材料力学の観点から詳しく見ていきます。

曲げ変形を分解して考える

支柱に支えられた棒に荷重を与えたとき、棒は荷重方向にたわみます。曲げと呼ばれる現象です。立橋などの構造物も目視できるレベルではありませんが、発生している変形は曲げの範疇に含まれます。

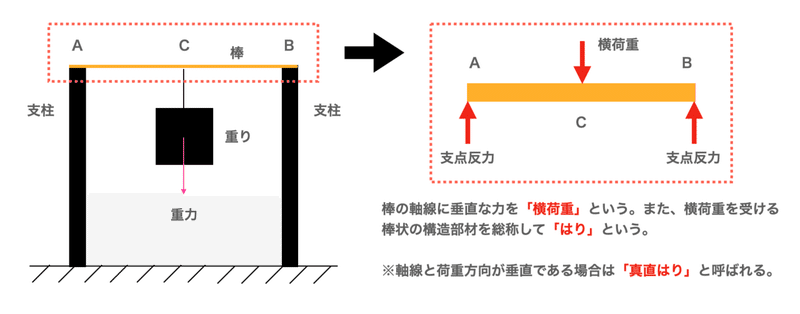
棒がたわむことに対する抵抗として、棒の内部には応力が発生します。これを「曲げ応力」と言います。曲げは引張と圧縮が不均一に作用する変形ですが、中立面を境に引張と圧縮が分かれます。

材料力学では「はりの横断面は変形後も平面を保つ」という仮定を用います。この仮定は「ベルヌーイ・オイラーの仮定」と呼ばれる重要な考え方で、はりが均質で大きなたわみを生じない場合に成立します。

ねじり変形を分解して考える

回転が拘束された棒をねじると、棒には変形抵抗として棒の軸線に垂直な面に円周方向の応力が発生します。ねじりと呼ばれる現象です。

ねじりが作用すると、棒には変形抵抗として棒の軸線に垂直な面に周方向に応力が生じます。この応力の合力はゼロですが、合モーメントはゼロにはなりません。このモーメントを「ねじりモーメント」と言います。

曲げの時は横断面に引張と圧縮が作用していました。これは横断面に対して垂直方向に内力が発生しているからです。ねじりは横断面に対して平行方向に内力が発生するため、せん断になります。

ねじり変形においても、材料力学としての仮定があります。ねじりモーメントが作用する前後において、横断面は平面を保つことです。

この仮定に基づいて横断面でせん断が不均一に作用することで、ねじり変形に至ります。横断面の各点は中心軸からの距離に比例した量だけ回転することで、ねじりモーメントが成立するのです。

部材の剛性を決める定数

部材の曲げやねじりに対する抵抗性能を知ることは、機械や建築物の設計において大切な作業です。これは主に次の定数で決まります。

・ヤング率：材料固有の固さ
・断面二次（極）モーメント：断面形状で決まる固さ

例えば、材質の観点で見ると、ゴムよりも木材の方が曲げにくいです。これはゴムより木材の方がヤング率が大きいことが理由です。

断面形状の観点で見ると、正方形とＨ形でも剛性は変わります。例えば、はり構造ではＨ鋼と呼ばれる部材が使われますが、これは同じ質量に対して正方形よりＨ形の方が断面二次（極）モーメントが大きいためです。

断面二次（極）モーメントに関しては、一般的な材料力学の書籍の付録として付いていることが多いので、そちらを参考にすると良いです。

おわりに

今回は変形の形態の中でも内容が複雑な曲げとねじりについて、引張・圧縮・せん断を基本として掘り下げてみました。

横断面では不均一な分布を示すので、実際の計算では積分の作業を伴うことが多いです。この辺は、実際に材料力学の参考書などを当たると良いです。

次回は解析分野でも度々用いられる「主応力」について解説します。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎