
ゆる~い電子回路 第1回:コンデンサ
突然ですが、「交流」についてどんなイメージをお持ちですか?
コンセントのやつ、何やら難しそう、式は追えるけどイメージがわかない…etc、といったところでしょうか。
交流理論なんてものは必要がなかったら一生触れないものであるのは間違いないですが、高校で物理をとったり、就職して配属された部署で回路の知識が必要になったりと、色々な背景でその入り口をまたぐ人がいます。
そして、自分の周りにも「交流が難しい」という困りごとを抱えた人が何人かいます。
彼らの声、そして初学者だった頃の私の声は次のような感じです。
曰く、「コンデンサに電気がたまるのはわかる。コイルが磁場を作ったり誘導電流が流れたりするのもわかる。が、交流で奴らが電流の位相を進めたり遅らせたりするのは何なのだ。」
曰く、「サインコサインが出てくるのはいい。exp(iωt)ってなんなんだ。」曰く、「共振…複素インピーダンス…あばばばば」
曰く、「ふくそへいめんじょうでやじるしがまわってるよー」
話をまとめると、交流はイメージがわきにくい上に、それを記述するための数学も難しいことで定性的な理解がしにくくなっているようです。
それで役に立つ本やサイトを探してみたのですが、案外定性的な理解を主軸に置いた文献が少ないことに気が付きました。
なら自分で書いてみよう、せっかく書くなら誰かの目に触れる可能性があるところに置こうということでNoteに投稿してみることにしました。
言語学のトピックからは外れますが、少しの間お付き合いいただけると幸甚です。(そちらはそちらで投稿継続します。)
■「電気をためておく」ということ
コンデンサは電気をためておく素子です。
しかし、交流になった瞬間その説明はどこへやら。「電圧に対して電流の位相をπ進める素子」へと豹変して多くの初学者を苦しめます。
実はコンデンサ自体がやっていることは直流でも交流でも変わりません。
ただ一つ、「電気がたまること」をちょっと突き詰めて考えるだけで直流でのコンデンサのふるまいも交流でのふるまいも一緒に理解することができます。
ということで、今回は「電気をためるもの」という特徴から、コンデンサの電流電圧特性まで一歩ずつ考えてみたいと思います。
■電気をためるものの歴史
まずは電気がたまるのはどういうことか、ざっくりイメージを持つために人がどのように電気をためる素子を理解してきたかの歴史を見てみましょう。
1750年ころ、世界各地で次のような発見がなされました。
水の入った瓶に手を触れ、水中に電極を垂らしてその電極に電圧をかける。
電源を外した後に電極に手を触れるとバチっとなって痛い。
どうやら、こうすると水と手の間に電気がたまるらしい。

この発見は、最初にこれを発見された場所とされるオランダのライデン大学にちなんでライデン瓶と名づけられました。
また、物理学者であったダニエル・グラードはこのライデン瓶を並列につなげて「砲兵中隊 (=Battery)」と呼び、これがバッテリーの語源となりました。
発見からほどなく、この瓶の本質が「導体の間に絶縁体を挟むことで電気をためられるようになる」ことであるとベンジャミン・フランクリンによって指摘されました。
そしてフランクリンはこれを改良して、次のような「電気をためる瓶」を作りました。
これが今日広く知られるライデン瓶です。
プラスチックのコップにアルミを巻いたものを重ねたものを授業などで触ったことがある人も多いかと思いますが、あれと全く同じです。

(フランクリンの絵ではないが、オープンソースの絵の中で一番わかりやすかった。)
フランクリンは後にこの瓶と凧を使った有名な実験を行い、雷の正体が電気であることを発見します。
この発見によって、フランクリンは避雷針という偉大な発明をすることになるのですがそれはまた別の話。
そして1775年頃、このライデン瓶のアイデアは「ボルタ式電池」を発明したアレッサンドロ・ボルタによって洗練され、「ガラスを挟んで電極を対向させたものに電気をためる」形が生まれました。
彼が考案した「電気をためるもの」は、次のようなイメージです。

ボルタは、電気を「凝集したように」たくさん溜めるというニュアンスを込めて、これを「コンデンサトーレ」と名付ます。
このコンデンサトーレは、名前も構造も今日のコンデンサとほとんど同じです。
しかし、このコンデンサートーレやライデン瓶が人々の生活と密接にかかわるようになるまでは、それからおおよそ100年待たなければなりませんでした。
ライデン瓶は実験器具や瞬間的に高い電圧をかけるための装置としては重宝されていたようですが、応用は限定的で一般向けには電気の概念を面白く伝える教材や出し物以上の役割を持たなかったといいます。
コンデンサーがなくてはならないものになったのは、無線通信が発達するようになってからです。
■無線通信とコンデンサー
世界初の無線通信は、1887年にハインリヒ・ルドルフ・ヘルツが、一つのライデン瓶が放電したときに別のライデン瓶も放電したことに気が付いたのがきっかけでした。
このころには既にマクスウェルによって電波の存在が予言されていましたが、それが初めて実験的な事実と結びつけられたのがこの瞬間でした。
(マクスウェルの方程式の発表が1868年。)
が、コンデンサが無線通信において重要になったのはこの放電によるものではありません。放電させるだけならコンデンサやライデン瓶よりもいい方法はいくらでもあります。
コンデンサがその真価を発揮したのは、もっと本質的な問題に対してでした。
それは、周波数の制御です。
空気による電波の吸収の都合で、長距離通信に適した周波数というものが存在します。
そこの周波数を狙って電波を飛ばさないことには安定した通信は困難です。
しかし、放電現象で生じる電波はある種のノイズのようなものであり、特定の電波を強く放出させるためには工夫が必要でした。
ここで強力な役割を果たしたのが、「コンデンサとコイルを直列につなぐと特定の周波数の電流だけよく流れる」という性質です。
ヘルツはすぐにこれに改良を加え、発生したノイズから、「コンデンサとコイルを直列につないだフィルタ」で特定の周波数だけを取り出すことで解決しました。
その回路でそのまま放電させることはできないので、フィルタに使ったコイルの横に別のコイルを置き、そちらに誘起される同じ周波数の誘導起電力を使って目当ての周波数での放電を実現しました。

当時ヘルツは、「役に立たなくても別に良い。少なくともマクスウェルが正しいことの証明にはなった。」と語っていますが、ほどなくしてこの技術は無線によるモールス信号の送信という形で実用化されます。
余談ですが、放電によるノイズから欲しい周波数を取り出すタイプの無線送信機はアンテナ式に変わり、様々な場所で実用化されました。
そのに一つに、当時ジョン・フレミングが技術顧問を務めていたマルコーニの無線局があります。
このマルコーニの無線局というのは1912年タイタニック号の沈没事故においてタイタニック号から発せられる救援信号を最初に拾った無線局の一つであり、生存者を救助したカルパチア号とずっと無線でやり取りを行っていた局です。
瓶の放電現象にヘルツが気付きを得てからものの25年でそこまでの実用化が進んだことに、当時の社会の変化の速さや大きさが感じられます。
■コンデンサ
■静電容量
今日では、コンデンサは「絶縁体を挟んで向かい合った2枚の導体板」として紹介されます。
電荷をつないだ時の振る舞いは次のようになっており、前述の「ボルタのコンデンサトーレ」を簡略化したような格好になっています。

実際にこれを使いこなすためには、まず電圧をかけたときにどれだけの電荷が溜まるかを知る必要がありますが、ここについては良い本が多くあるので深く立ち入りません。
ただ「たまる電荷Qはかけた電圧Vに比例する(Q=CV)」とだけ紹介しておきます。
これは次のように考えると直感からもそこまで外れないです。
・電圧をかければかけるほど多くの電圧がたまりそう。
⇒Q ∝ V
・電極が大きく、距離が近く、間に帯電しやすいものを挟んだほうが多くの電荷が溜まりそう
⇒比例定数Cに押し込まれている。
■電荷がたまる間に流れる電流
さて、電流量は「単位時間当たりに通り過ぎる電荷量」で定義されていました。
コンデンサの場合、流れた電荷はすべて電極板のところにたまった状態になります。

すなわち、単位時間あたりの「たまった電荷の増分」が、そのまま流れた電流量になります。
これはシンプルに今の電荷量と、少し待った後の電荷量の差分をとり、待った時間で割れば求められます。

この⊿tを小さくすればするほど、リアルタイムでの電流量を知ることが可能になります。
この⊿tを限りなく0に近づけることが微分になります。

Cは一定なので、

となります。
■サイン波で考えてみる
前述のように、コンデンサが真価を発揮するのは交流電流の制御においてです。
交流は電流や電圧が波のように変動するものなので、ここでは電圧が一番シンプルなサイン波である場合を考えてみましょう。
V=sin(ωt)とすると、その微分はωsin(ωt)になるので、電流はωCsin(ωt)となります。
それを書いてみると次のようになり、電流のほうが電圧よりもπ/2だけ変化を先取りしているように見えることを指して、位相がπ/2進むと言います。

さて、ここまではどこかで聞いたような説明だと思います。
とても正しい説明なのですが、これでイメージわくでしょうか?
好きだったり事情があったりして数学の沼に肩まで浸かった人なら何も問題はないと思います。
しかし、冒頭お話しした通り本章は数学とイメージを結びつけるのに苦慮している人を想定して書いているので、こここそが掘り下げるべきポイントになります。
ともすれば「電流が電圧の変化量を先取りしている」とも取れてしまうこの表現による誤解を避けるため、微分の本質である「変化量」というところに着目して、電流と電圧の位相のずれが何なのか見ていきましょう。
■「π/2進む」をイメージする
このポイントが分かりにくいのは、やはり三角関数の微分というものが分かりにくいからでしょう。
そして、三角関数の微分が分かりにくいのは、サインとコサインを分けて考えているからです。
実際、次のように接線を引いて動かしてみても何やらよくわかりません。

では、これならいかがでしょうか?

(x=cosθ, y=sinθ)となる点は単位円を描きます。
そしてθが変わるとき、この点が動く方向は単位円の接線方向です。
この接戦方向のベクトルの、x成分がcosθの微分、y成分がsinθの微分になっています。
ここに簡単な補助線を引けば即座にわかりますが、この接線方向のベクトルは常にθよりπ/2進んだ方向を向いています。

すなわち、
・cosθのθに対する変化の割合はcos(θ+π/2)
・sinθのθに対する変化の割合はsin(θ+π/2)
に比例するのです。
これはそのまま、電流の電圧に対する変化の割合は、その位相をπ/2進めたものに比例すると言い換えられます。
高周波回路やフィルタを扱っていると、複素平面の中で点を回すことがよくありますが、波の位相を単位円上で理解することに慣れておくとすんなり入り口を通れるようになるでしょう。
■ちょっとだけ真面目に計算する
さて、先ほど「比例する」と言葉を濁しましたが、それは変化の大きさを全く確かめていないためです。
変化の向きだけわかってその大きさがわからないので、比例するとしか言えません。
ということで、ここからは少し真面目に横着しながら計算をしてみましょう。
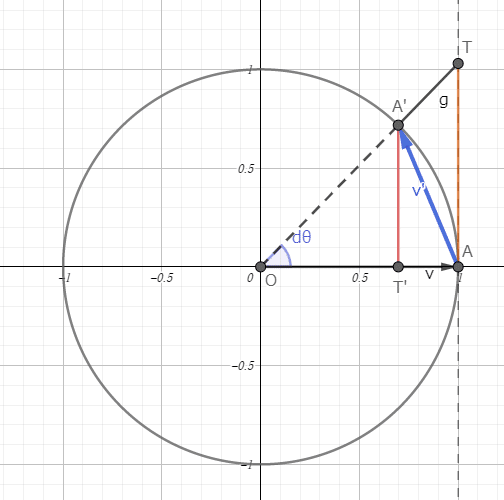
大きさを求めるために、θを⊿θだけ大きくしたときの変化量を考えます
図にするとこんな感じです。:

するとこの時vの微分は

で⊿θを限りなく0に近づけることでわかるので、大きさだけ考える場合は
弧AA'と線分AA'の長さの比を考えればよいことがわかります。
(単位円なので角度=孤の長さです。)
で、ここで最初の横着をします。
円の上なんてどこも同じなので、見やすいようにvをx軸の上に持ってきます。するとこんな感じになります。

で、ここで⊿θを0に近づけるのですが、まじめな計算はやってられないので次の横着をします。
まず、⊿θをどんどん小さくしていくと、線分AA'と弧AA'の長さの差はいかにも小さくなっていきそうです。
なんなら同じ長さにどんどん近づいていきそうです。
いやいや円周率だってそもそも円をどんどん細かい正多角形に分けて行っても止まったのだから、一緒になってくれないと困るのです。
と、駄々をこねていても仕方がないので、この辺でまじめな横着を始めます。
正直に線分AA'の長さを求めてしまうと、sin(⊿θ/2)と⊿θの大きさを比べるという苦行が発生します。
なら、同じになるもので内側と外側からサンドイッチしてやればよいのです。
はいドン。
外側のオレンジの線はtan⊿θです。
内側の赤い線はsin⊿θです。
この2つの長さが同じであれば、その内側にある折り返しを含まない線たちの長さは否応なく同じになります。
同じになるかが知りたいので素直に割ってみましょう。

⊿θを0に限りなく近づけていけば、これは1に限りなく近くなるので、外側の線と内側の線は同じ長さに限りなく近づきます。
すると線分AA'と弧AA'も同じ長さに限りなく近づくので、次の導関数の大きさは1になります。

ここで最初にした向きの議論を思い出すと、

となることがわかります。
おわりに
ということで、今回はコンデンサの特性を考え、その数学的な道具立てのイメージをちょっと整理したところで終わりにします。
読者と一緒に考え、その中で頭の中でイメージを作っていってもらうことが目的で書いているので、あえてキャッチーなまとめは書きません。
(書こうと思えば書けるとは言っていません。)
次回はコイルの話を少しかじりながら、おっかなびっくり交流理論に手を出した人が目を回す最大のポイント、"exp( i ω t )"が誰なのかについて触れていきたいと思います。
この文章はそもそも就職してから初めて回路と向き合わねばならくなる人を想定して書き始めたのですが、扱う製品が製品だけに多くの資料は読み手がある程度完成した回路理論の知識を持っている前提で書かれています。
その場合一番ワクワクするところをすっ飛ばして、そびえ立つ物理数学と過渡特性の壁と向き合うことになります。
それではなかなか面白くなって来ないので、ちょっと入門編から交流理論と過渡特性の資料が読めるようになるところまでをダイジェストでお伝えできる資料が作れないか、というのが本稿を書き始めたモチベーションですので、誰かの目に触れ、ちょっとでも勉強のハードルが下がったり面白い気がしてきたりしたらうれしいです。
非常に長く、マニアックな文章を最後までお読みくださりありがとうございました。
