ポール・ディラックの原論文を読んでみよう（1925年：量子条件の導出）

ディラックの論文の一覧があります。1948年までのものが書籍化されていて、そのもくじがこちら。

今回取り上げるのは、上のリストで「PART 2: The golden years」（黄金期）とある章の最初にでてくる「1925.3」の "The Fundamental Equationa of Quantam Mechanics"。量子力学にポール・ディラックありと世に知らしめた、最初の画期です。ちなみに当時は院生さんで、博士論文を提出するより以前のものです。

ちなみに上の論文リストに「1925.3」とあるのは「1925年に受理された論文のうち3本目」の意です。同年11月7日に受理されていますね。

出だしを見ていきましょう。

It is well known that the experimental facts of atomic physics necessitate a departure from the classical theory of electrodynamics in the description of atomic phenomena. This departure takes the form, in Bohr’s theory, of the special assumptions of the existence of stationary states of an atom, in which it does not radiate, and of certain rules, called quantum conditions, which fix the stationary states and the frequencies of the radiation emitted during transitions between them. These assumptions are quite foreign to the classical theory, but have been very successful in the interpretation of a restricted region of atomic phenomena. The only way in which the classical theory is used is through the assumption that the classical laws hold for the description of the motion in the stationary states, although they fail completely during transitions, and the assumption, called the Correspondence Principle, that the classical theory gives the right results in the limiting case when the action per cycle of the system is large compared to Planck’s constant h, and in certain other special cases.

以下はDeepLによる日本語訳：

原子物理学の実験的事実が、原子現象の記述において古典的な電気力学の理論からの逸脱を必要とすることはよく知られている。 この逸脱は、ボーアの理論では、原子が放射しない定常状態の存在と、その定常状態と定常状態間の遷移中に放射される放射線の周波数を固定する量子条件と呼ばれる特定のルールという特別な仮定の形をとっている。 これらの仮定は古典理論とは全く異なるものであるが、原子現象の限られた領域の解釈においては非常に成功している。 古典理論を用いる唯一の方法は、遷移時には完全に失敗するが、定常状態での運動の記述には古典法則が成り立つという仮定と、対応原理と呼ばれる、系の1サイクルあたりの作用がプランク定数hに比べて大きい場合の限定的な場合、および他の特定の特殊な場合に、古典理論が正しい結果を与えるという仮定である。

「ボーアの理論」とあるのは、これです。中学の理科で習うアレ。高校でも習うの。

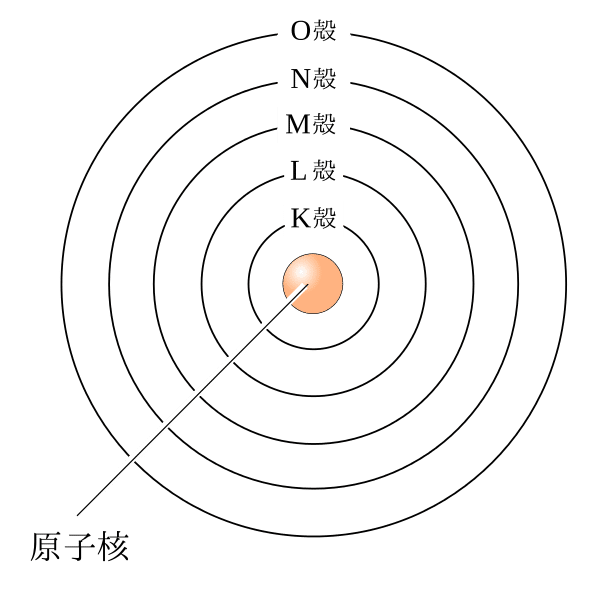
中学高校で習うものでは、こうやって真円で図解されていますが、実は楕円でも成り立ちます。ボーアのこの理論（1913年）をもとに、ゾンマーフェルトが当時の前衛数学を駆使して、こんなんでもいけまっせーと提唱したのがこれ。

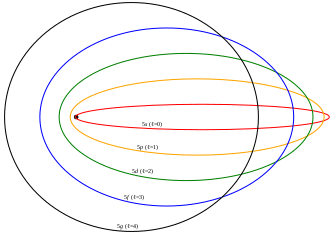
これはボーア＝ゾンマーフェルトの量子化条件と呼ばれています。1916年提唱。こういう楕円軌道でも成り立つとすれば、それまでボーアの真円理論では説明できなかったいくつかの実験データを、うまく説明できるということで、この楕円理論は歓迎されたのです。

ただ、この理論をもってしても解けない謎が残りました。「そもそもなんでこんな風に電子の軌道はとびとびになるねん？」という素朴な疑問です。

ボーアの理論は、実験データをうまく説明するには電子軌道がとびとびになっていると仮定すればいいと、半ば決めつけのアイディアで生まれたものでした。しかしシンプルな数式から電子に関する実験データに沿う値を出せるので、こりゃあ便利だわと急速に受け入れられたのです。ゾンマーフェルトによる楕円化にしても、ボーアの決めつけアイディアを元にしていることに変わりはなくて、結局この軌道とびとびの理由は説明できないままでした。

ここでディラックの論文に戻ります。先ほど引用したぶんの続きです。

In a recent paper Heisenberg puts forward a new theory, which suggests that it is not the equations of classical mechanics that are in any way at fault, but that the mathematical operations by which physical results are deduced from them require modification. All the information supplied by the classical theory can thus be made use of in the new theory.

DeepL訳：

ハイゼンベルクは最近の論文で、古典力学の方程式に何らかの欠陥があるのではなく、そこから物理的結果を導く数学的操作に修正が必要であるという新しい理論を提唱している。古典的理論が提供する情報はすべて、新しい理論で利用することができる。

同年1925年に、ボーアの愛弟子のひとりヴェルナー・ハイゼンベルクが、あるとんでもなく前衛的な論文を刊行していて、そのゲラがディラックのもとに（彼の指導教官から）送られてきました。ドイツ語で書かれていたので読むのに多少難儀しながらも、ポールくんは内容の大胆さに驚きました。内容を要約すると「だいたい電子の軌道などというものを誰が確認したというのだ？ 測定可能な値のみに基づいて議論を進めるべきだ」と宣言した後、小難しい計算式が延々と続いていく、そういう内容でした。

写実的ではない、抽象絵画にGOだぜ！というところです。

ポールくんは当初、この論文にだらだらと連なる計算式のだらだらぶりに閉口して、しばらく放っていました。しかし十日ほどして再読してみると、その中盤にちらっと面白いことが書かれているのに気づきました。「ＡとＢを掛けるのと、ＢとＡを掛けるのでは、値が違ってくる」　具体的にいうと位置×運動量と、運動量×位置では、同じ掛け算なのに違う値になるというのです。

ヴェルナーくんは当時、この不可思議な算数についてうまく説明できなくて、論文のなかでは深入りしないで話を進めています。ところがポールくんはこの指摘に大興奮しました。なにしろ無口の極みみたいな彼が、このときはママンに向かって「これはどえらいことである！」と熱弁したというぐらいです。

彼は数学大得意マンでした。ＡＢ≠ＢＡとなる数学についても心得がありました。ハミルトン四元数やグラスマン代数のことです。当時の物理学者でこの両方に精通しているひとは、ほとんどいなかったと思います。ポールくんは四元数をすでに独習していて、グラスマン代数についてもお茶会セミナーで聞き知っていたので、すぐぴんときたようです。

当初彼は、ヴェルナーくんの論文の欠陥が、特殊相対論に対応していないことにあるとみました。この世のあらゆる物理法則を統べるエンペラー・特殊相対論。それに沿うよう、ヴェルナー論文を改良できないか、いろいろ試してみたものの、うまくいかなくて、そこでＡＢ≠ＢＡについて思索していく方針に切り替えました。

ちなみに彼（ポールくん）は当時院生の最後の年でした。

ある日曜のこと、散歩中に彼の脳裏をよぎったものがありました。「まてよ、ＡＢ－ＢＡとある数式、ハミルトン力学に出てこなかったか？」 翌日つまり月曜の朝、大学図書館に駆け込んで "Analytical Dynamics of Particles and Rigid Bodies"（1904年刊行、その後何度か改訂）という名著を棚から引っ張り出してＡＢ－ＢＡを探してみたら…

ポアソン括弧式と呼ばれるものがそこにはありました。

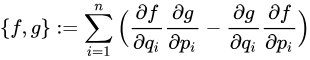
これは位置と運動量の関係がＡＢーＢＡ≒０であることを示す式です。ハミルトン力学を支えるレンガのひとつで、これは天体力学にも応用できる優れものでした。

ポールくんの論文を見ていくと… でてきますね。

後にこの数式はもっとシンプルに

px - xp = (h/2πí)Ｉ

と書き改められます。この素朴な式より、ボーア理論では説明できなかったとびとび現象をきれいに導出できると、ポールくんは言い切ったのです。

この画期的論文は1925年11月7日に受理され、12月1日に刊行されています。実はその少し前、11月23日に、ヴェルナー・ハイゼンベルクはポール・ディラックに宛てて便りを送っていました。この論文の校正刷りを、ポールがヴェルナーに送っていて、それに目を通したヴェルナーがびっくりして、数日後つまり23日にポール宛てに２ページの、ドイツ語による書簡を送っています。「あなたの論文すげーびっくりしたが、自分の師匠のひとりマックス・ボルンが（ヨルダンの手助けで）同じ結論の論文を二か月ほど前に書いている」

これにはポールもびっくりだったようです。ただ、ボルンが算出した量子条件式は、彼のものよりもっと野暮ったくて、行列を使っていました。

ＰＸーＸＰ＝ (h/2πí)Ｉ

今では高校数学で基礎を習う「行列」も、この時代の物理学者には前衛数学でした。事実ディラックもハイゼンベルクも学校で習っていなかったのですが、年長のボルンはたまたま多少習ったことがあって、さらには数学に強い歳若の協力者ヨルダンの手助けもあって、行列を駆使してこの式を捻りだしたのです。

違うやり方で同じ形式の数式が導出できることに、ディラックは驚いたことと想像します。面白いのは、彼がこれをきっかけに行列を使っての研究に進むどころか、むしろ違う代数の構築を目指したことでした。

３×４と４×３が一致しない代数体系… そういうものが成り立つ数を「q-number」（ｑ数）、反対に３×４と４×３が一致するのを「c-number」（c数）と名付け、それまでの物理学は c 数準拠だから q 数で考えていけば量子力学対応に進化させられると考えたのです。

このアイディアは、今回取り上げた論文よりもう少し後のものから活かされていきます。ハミルトン力学はまさにこの代数体系を内在させていて、また天体力学でいう「摂動」の解を求めるのに有効でした。ポールくんはポールくんで公的な初論文ですでにハミルトニアンを使って原子の電子変移を説明できるのではないかというアイディアを出していました。ｑ代数とでもいうべき代数体系をもってすれば、量子力学を簡潔明瞭に語り切れる…そう信念を強くしたのです。

ハイゼンベルクからの便りには、ヨルダンやパウリや、ほか何人もの天才たちがこのフィールドで先頭争いを繰り広げていることも綴られていました。彼らは常に連絡を取り合って、切磋琢磨しながら最新研究を続けていると。ケンブリッジで独り思索にふけりながら真理ににじり寄っていくポールくんも、このとき自分の立ち位置を意識したようです。

ゆけ孤高の天才！ ボーア一派＆ゲッチンゲン数学を相手に、君は生き延びることができるか！？