
「SuperだけどTic-Tac-Toeでない」を考えてみた。
この記事はアブストラクトゲーム Advent Calendar 2023の11日目の記事として書かれました。
はい、どうも。
珍ぬと申します。
4年半近く、noteでボードゲームやパズル関連の記事をかれこれ300本書いています。
去年に引き続き、アブストラクトゲーム Advent Calendarを立ち上げました。
前回の記事、
で「Super Tic-Tac-Toe」を拡張してヒドイことになりました。
今回は拡張せずに、ルールの差し替えをします。
「Tic-Tac-Toe」しません
まず、「Tic-Tac-Toe」を抜いてしまいます。
そこからできるだけシンプルなルールに差し替えます。
で、ポッと思いついたのが
・手番では、盤面のマスを1つだけ削っていく(言い換えると、コマは1種類のみでコマを書いていく)
・盤面はひとつながりでなくてはならない(言い換えると、コマの連結によって、盤面を2つ以上に分断しない)
です。
盤面の連結ですが、タテヨコのみ繫がっていることとして、ナナメは繋がらないとします。
つまり、交互に手番を行い、盤面を分断してしまうと負けになります。
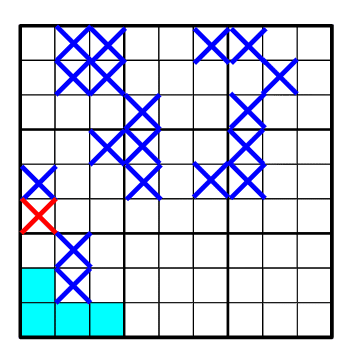
上の盤面はプレイ例です。
青の×が削ったマス、赤は直前に削ったマスです。
次の手番は、左下(3×3の〈小盤〉)の範囲となります。
手番のプレイヤーは、水色のマスを削ってしまうと盤面のマスがひとつながりにならないので、これら以外のマス(3つ)を削ることとなります。
ですが、実はほかにも勝敗条件を考える必要があります。
簡単な先手必勝でした
それは「マスが全て削られた(あるいは、すべてのマスにコマが書かれた)状態の〈小盤〉」の扱いです。

9マスすべて削った状態です。
当然、手番になってこの〈小盤〉を指定されると、削る(あるいは書く)ことはできません。
その場合は、手番のプレイヤーが負けとなるとするのが自然でしょう。
ところがですね、この条件だとシンプルに先手必勝なのです。
例を出してみます。
初手の先手は、後手に再び同じ〈小盤〉で削る(あるいは書く)ようにします(候補のマスは、赤色のマスになります。今回は左上とします)。

後手は、残りの8マスから選んで削り(あるいは書き)ます(今回は中央とします)。

次の先手ですが、また初手の〈小盤〉に戻る位置のマスを削り(あるいは書き)ます。

はい、これを繰り返すと結果は、

後手は最後のマスを削ったあと、次の先手は水色のマスを削れば、後手が削れるマスがありませんので負けが決定です。
なので、このシンプルな戦法をとることができないようにしてみます。
手番のプレイヤーは、「マスが全て削られた(あるいは、すべてのマスにコマが書かれた)状態の〈小盤〉」に誘導するような手を禁止します。
つまり、上の図例だと、水色のマスは削ることができなくなる、ということです。
多分ゲームになっているかも
禁止事項のルールを加えたことで、試しにプレイしてみました。
おそらく、シンプルな必勝法をかなり回避していそうです。
極端な例ですが、「マスが全て削られた(あるいは、すべてのマスにコマが書かれた)状態の〈小盤〉」を次々と優先的に作っていくようなプレイをするとどうなるか。
たとえば左側の〈小盤〉を1列すべて削ることを目指してみます。

左側27マスのうち25マスを削っています(青)。
一方で中・右側の〈小盤〉でもマスを削っています(赤)。
さて、次の手番は左下の〈小盤〉となります。
2のマスを削ると、1のマスが盤面全体から分離してしまいます。
なので1のマスを削る1択となります。
その次の手番は左下の〈小盤〉。
3のマスを削ると2のマスが盤面全体から分離してしまいます。
ということで、タテ・ヨコ・ナナメ1列に並んだ〈小盤〉3つを削ることはできないようです。
【追記:2023/12/17】
上の図は、実は間違っていてルール上不可能です。
修正した図をフォローの記事(Advent Calendar17日目)に描きました。
大変申し訳ございませんでした。
必勝法は存在します(なにせそれがアブストラクトゲーム)が、完全解析するにはにいささか骨を折らせるかと思います。
マスの形状を変える
さて、今回考えたルールだと、〈小盤〉のサイズは3×3限定で無くても遊ぶことはできます。

マスの形はなにも正方形でなくてもよいのです。
Hex(正六角形)でも「マスの連結は辺で接している」として、うまい具合に〈小盤〉をつくることができれば、置き換え可能です。

Triangle(三角形)でも可能ですが、いくつかの〈小盤〉は回転したり裏返したりの配置となるため、どの方向が上(方角で例えると北)なのかを考えなければなりません。
番号や記号などを付けることで、ミスを防ぐサポートとなります。

右上図は、盤面全体のサポートとなります。
Hex(正六角形)も1つの〈小盤〉のマス数を変えると、下のような盤面を作ることができます。

右図は、盤面全体のサポートとなります。
前回の記事で書いた、これらの「SuperSuperSuper〜」化もできますが、精神的健康のため止めるのが無難です。
締め
ということで、考えてみました。
そういえばこのゲームの名称を決めておりませんでした。
1種類の記号のみで変則「Tic-Tac-Toe」を遊ぶ「Notakto(ノタクト)」があります。
今回は盤面を分断すると負けとなるので、接続の「Connect」と「Notakto」を合体して、「Super Nonnect(スーパーノネクト)(仮)」としてみます。
まだまだアブストラクトゲームAdventCalendar2023は続きます。
引き続きよろしくお願いします。
では。
……では?
