
三平方の定理から三角比へ
さて、今回は中学校3年生で学習する「三平方の定理」と、高校数学Ⅰで学習する「三角比」に、どうすればスムーズに発展させていけるか考えてみます。
最後まで読んでいただけるとうれしいです!!
1 三平方の定理とは
三平方の定理とは、次のような直角三角形の3辺の間に成り立つ関係式です。

この式から読み取れるのは、2つの辺の長さが分かっていると、1つの辺の長さを求めることができるということです。
例えば、下のような直角三角形で斜辺以外の2辺の長さが分かっていれば、斜辺の長さを求めることができます。

2 特別な直角三角形
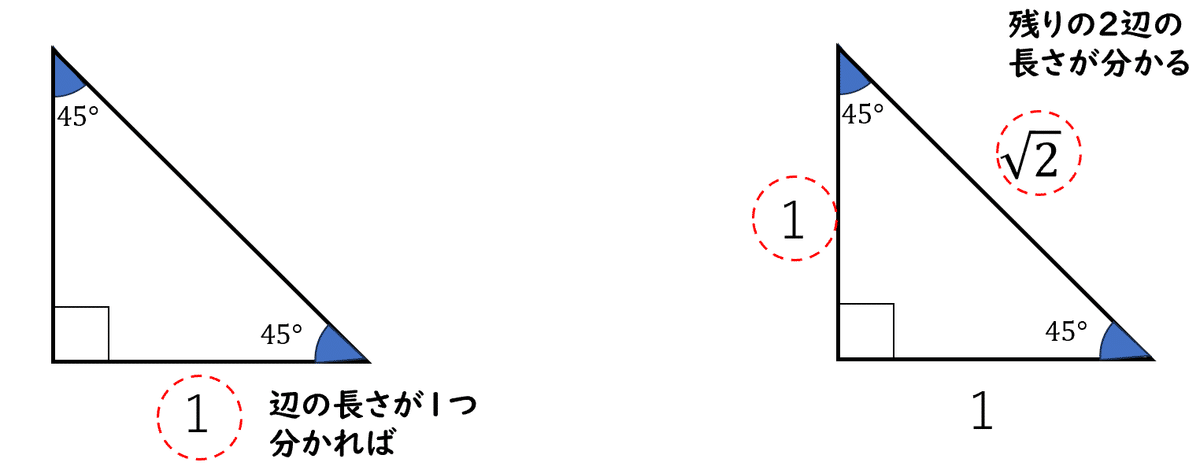
中学校3年生では、三平方の定理の単元で、次のような特別な直角三角形について考察します。

何が特別かというと、内角の大きさがすべて分かっているというところです。
そしてこの特別な直角三角形の場合、辺の長さが1つ分かれば残り2つの辺の長さが分かります。

ここまでが中学校3年生の単元「三平方の定理」で学習する内容です。
もう一度、この単元で何をしていたのかまとめます。

さて、この図を見たとき、次のような疑問が自然と湧いてきませんか?
内角の大きさがこの組み合わせ以外のときは、残りの辺の長さが分からないのだろうか?
3 高校数学Ⅰ「三角比」
上述した疑問を解決するために、過去の数学者たちが頑張って作ったのが三角比表ですね。
例えば、内角の大きさが90°、70°、20のときは、三角比表を活用すると、残りの2辺が分かります。

ここまでは直角三角形という特別な三角形で考察しました。
図でまとめます。

次に、この図を見ると、また疑問が湧いてくるんです。
直角三角形でなければ辺の長さは求められないのか?
4 正弦定理と余弦定理
上の疑問を解決するのが、正弦定理と余弦定理ですね。
この2つの定理を活用すれば、直角三角形でなくても辺の長さを求めることができます。
5 おわりに
今回の記事で書いてみて思ったんですが、辺の長さを求めるために、数学は特殊から一般へ、先人が必死に編み出した定理を系統的に学んでいたんだと実感しました。
このように教科書を俯瞰してみるのも面白いですね!
最後まで読んでいただきありがとうございました!!

