
二次方程式の解き方
1 二次方程式とは
二次方程式とは、
$${ax^2+bx+c=0}$$ ただし、$${a}$$は0ではない
で表される方程式です。
たとえば、
$${x^2+2x-3}$$
という方程式は、二次方程式です。
2 二次方程式の解き方
教科書を確認すると、二次方程式の解き方は3つ紹介されていました。
1 平方根の考え方を用いる方法
2 因数分解の考えを用いる方法
3 解の公式を用いる方法
3 平方根の考え方を用いて解く
$${m}$$の平方根とは、2乗して##{m}$$になる数です。
例えば、
1の平方根は、±1
2の平方根は、±$${\sqrt{2}}$$
です。
平方根については、二次方程式の1つ前の単元で学習します。
平方根の考えを用いて解くことができる二次方程式は、
$${x^2-2=0}$$
$${2x^2-10=0}$$
のようなものです。

4 因数分解の考えを用いて解く
因数分解とは、和の形で表されている文字式を積の形に変形する方法です。

因数分解を用いるとなぜ解けるのかというと、掛け算における0がもつ特徴があるからです。

この特徴を使わないと、次のように解を見つけることになります。

このように、手間がかかります。また、上の例でいうと、この二次方程式の解が$${x=1}$$以外にあるかどうかもわかりません。
それに対して、因数分解を用いれば解を効率よく求められます。また、解が2つしかないことも一目瞭然です。

5 解の公式を用いて解く
例えば、次の二次方程式の解を求めることを考えます。
$${x^2+x-1=0}$$
平方根の考え方を用いるには、式の形が$${x^2-a=0}$$でなければいけません。しかし、与えられた二次方程式には$${x}$$の項があるため用いることができません。
因数分解はどうでしょうか。これも因数分解をするための2つの数の組がすぐには見つかりません。
では、この二次方程式を解くことはできないのか?
いえ、解けます。
平方根の考え方が使える形に変形します。
平方根の考え方を使うには、次の式の形に変形できればよいわけです。
高校では、この変形を「平方完成」といいます。

実際には、次のようにします。

ただ、上述した操作を毎度毎度するのは手間です。
そこで、公式にしちゃえ!!ということで、解の公式が示されます。
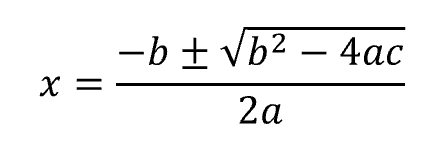
6 平方完成の図形的意味
よく生徒から、平方完成の意味が分からないという質問がでます。
たしかに、数学が苦手な生徒にとっては、難しい部分です。
そこで私は、平方根を求めることは正方形の一辺の長さを求めることと同値、という既習事項とつなげて説明します。

では、平方完成の図形的意味です。

平方根の単元の学習内容とつなげることで、系統性も出てきます。
この説明をすると、「なるほど!」という反応をしてくれます。
7 最後に
このような教材研究をして、授業に臨みました。
もし、他にも良い方法や、不足している考えがございましたら、ご教授いただけると、幸いです。
最後まで読んでいただき、ありがとうございました。

