
数学のよさを実感できる教材を考える ~結果の美しさを実感させることを通して~
1 数学のよさとは
「数学のよさ」とは,例えば「数量の関係を方程式で表すことができれば,形式的に変形して解を求めることができる」といった数学的な表現や処理のよさや,数量や図形などに関する基礎的な概念や原理・法則のよさ,数学的な見方・考え方を働かせ ることのよさなどを意味する。
今回は、上述した3つのよさのうち、数学的な表現のよさを実感できるようにしたいと思います。
私は、数学的な表現のよさを実感させるためには、表現して見えてくる美しさを感じさせることを提案します。
人は、規則性があると美しく見えるものです。
その教材として、n÷7はどうでしょうか?
2 整数を7で割ると?
さて、整数を7で割った商を考えてみます。
まずは、1~6を7で割ってみます。
・ 同じ商が繰り返し現れる美しさ
$${1÷7=0.142857142…}$$
$${2÷7=0.285714285…}$$
$${3÷7=0.428571428…}$$
$${4÷7=0.571428571…}$$
$${5÷7=0.714285714…}$$
$${6÷7=0.857142857…}$$
お気付きになるとおもいますが、割られる数が変わっても、
商は数列{1,4,2,8,5,7}が現れて、この順番は変わりません。
その理由は、下の図1のように、7で割った余りが同じように現れるからです。(色の規則性を見ていただくと、分かりやすいと思います。)


・ 商に{0,3,6,9}が現れない
この商が現れない理由を考えてみても面白いです。
7×3、7×6、7×9の一の位に秘密があります。
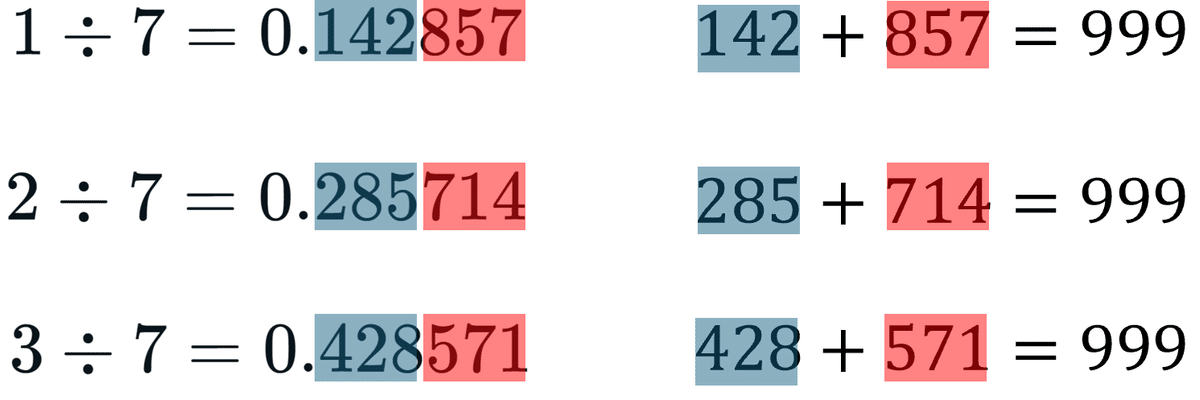
・ 循環列を半分にして足すと、9が並ぶ美しさ
下の図のように、循環列を半分にして足すと、9が並ぶという美しさが見られます。
3 発展的に考える
今回は「7」で割りました。
では、他の数で割った時に同じような美しさが見られることはないでしょうか?
このように、発展的に考えようとするのではないでしょうか。
この教材は、割り算という、どんな生徒にも取り組める内容です。
4 最後に
そもそも、美しさを求めようとするのは、人間が生まれながらにもっている有能さです。
これは、我が子の様子を見ていても感じます。
先日、戸棚に置いていた激落ちくんを袋から出して一列にきれいに並べて、拍手していました。
まだ2歳にならない子がです。
これを見ても、人間は美しさを求めようとします。
この力を活用して、数学のよさを感じさせたいですね。
最後まで読んでいただき、ありがとうございました。

