
私立中高一貫校の学力平均回帰と深海魚発生のメカニズム③(後編)
一定の前提条件による仮想の都道府県に対して、私立中高一貫校と公立中学・高校の学力分布モデルを作り、中高6年間の学力変化のシミュレーションを行っています。過去2回の分析で、次の点を確認できています。
成績が正規分布に従う場合、私立中高一貫校でも公立中学・高校でも、生徒全体の平均学力は中高6年間の中で学年全体平均に回帰する。
中高6年間で学力増減が起こるのであれば、学校別に見ると、私立中高一貫のトップ校だけでなく、公立高校のトップ校でも、学力平均回帰と深海魚発生の傾向は同様に存在する。
ただし、学力レベル別の学校への層別が早く行われる私立中高一貫トップ校(層別から6年間)の方が、公立トップ校(層別から3年間)よりも、学力平均回帰と深海魚発生がより顕著に現れる
今回はこのシリーズの完結編として、これまでの分析結果を元に、学力平均回帰と深海魚発生のメカニズムについて考察します。
0. まとめ
中高6年間で学力増減が私立でも公立でも均等に発生する場合、ある時点の学力が直前の学力に依存(非独立)するなら、
時間とともに学年全体の学力格差が拡大するため、私立中高一貫校の相対的な学力レベルは学年全体平均に回帰する。
私立中高一貫のトップ校では中学入学時の学力起点が高い故に、深海魚が発生する。
単に学力面だけで見るなら、大学受験のために「私立中高一貫校に入学すること自体」には、経済合理性がない。
逆に言えば、私立中高一貫校でも大学附属校や鉄緑会の指定校などでは、「私立中高一貫校に入学すること自体」に意味がある。ただし、その分の入試難易度のプレミアムが乗るため、経済合理性はプレミアムの個人的評価に依存する。
また、中学受験であれ先取り学習(英語など)であれ、小学生のうちに学力レベルを上げておくことは、難関大学の合格にはメリットが大きい。
1. 学力平均回帰のメカニズム
前編での分析の結果、私立中高一貫校と公立中学・高校の平均偏差値の推移はこのグラフのようになっていました。

また、中編でシミュレーションした学校別の平均偏差値をグラフにすると、こうなります。私立のトップ5校(50校中)を抽出しています。

どちらも、平均偏差は時間の経過とともに全体平均の50に回帰していることが確認できます。
ところが、今回のシミュレーションでの学力増減は直前の点数を起点に正規分布で変動させているため、学校ごとの平均点は時間経過しても変化しない設計にしています。言い換えれば、学校平均の絶対的な学力差は入試(学校レベルの層別)があった時点と同じ差が維持される前提となっています。
例えば、私立トップ5校の学校平均点の推移はこのようにフラットです。学校間の平均学力の差を入試時点の差から埋める/広げる具体要因が見つかっていない以上、前提としてはそれほどおかしくないと考えます。
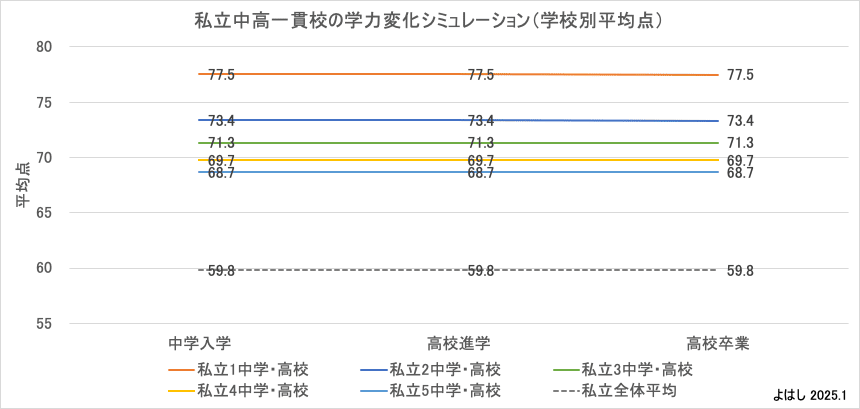
これを是とすれば、平均点という絶対指標は入試時点の差が学校間で維持された状態で、平均偏差値という相対指標は平均回帰するのは、標準偏差が拡大しているのが要因です。
前編で行った分析を改めて見直すと、母集団全体の点数分布は時間の経過とともに拡大しています。これは私立だけでなく、マジョリティの公立も含まれています。

これまでの考察をまとめると、この図のようになります。

中高6年間で学力増減が存在する場合、ある時点の学力が直前の学力に依存(非独立)なら、右上のグラフの推移のように、時間経過とともに学力差は拡大します。その結果、学年全体の標準偏差も増加します。
一方、私立中高一貫校の絶対的な学力差(点数)が中学入学時点から変わらないのであれば、母集団の標準偏差の拡大とともに、平均偏差値は下がっていきます。言い換えると、相対的な学力の優位性は時間の経過とともに圧縮されいくと言えます。
このメカニズムが、私立中高一貫校の学力平均化のメカニズムと考えられます。
2. 深海魚発生のメカニズム
「深海魚」というのは受験業界で用いられる表現で、雑誌の記事では次のように定義されています。
中学受験を経て中高一貫校に進学したものの、成績がさっぱり伸びずに下位をさまよう子がいます。 そういう子を中学受験業界では、ひそかに「深海魚」と呼んでいます。
この「深海魚」の定義には、「相対的深海魚」と「期待値深海魚」の2つの意味が混じっていると考えます。
相対的深海魚
同じ学校(標本)の中で、成績が下位をさまよう生徒期待値深海魚
学年全体(母集団)の中で、高校卒業時において、中学入学時の学力レベルから期待される学力レベルにない生徒
相対的深海魚は私立中高一貫校に限らず、公立中学でも公立高校にも存在します。
一方、期待値深海魚は「中学受験で難関中学に入学したら、当然、高校卒業時にも高い学力レベルにあるはず(=難関大学に合格するはず)」という先入観に対して、「高校卒業時の絶対的な学力レベルが期待値に届いていない(=難関大学に合格できない)」ケースのみ存在します。そのため、一定レベル以上の進学校にのみ期待値深海魚は存在します。
今回の分析での、「深海魚」は「相対的深海魚 かつ 期待値深海魚」として定義します。具体的には、「中学受験を経て私立中高一貫校のトップ校に入学したのに、成績が学校内の下位(相対深海魚)にあり、高校卒業時にMARCH以上に合格できる学力レベルがない(期待値深海魚)ような生徒=深海魚」です。
そこで、シミュレーションした私立中高一貫校の上位3校について、中学入学時の学力レベルごとに高校卒業時の学力レベルがどのように分布するかを見ていきます。
なお、このモデルでは私立中高一貫校は50校(全200校中)のため、その上位3校は東京の私立中781校(令和6年度学校基本調査より)でみると上位11校に相当します。
また、MARCH以上の学力レベルは学年全体の偏差値60以上(学年上位16%=学年120万人なら約20万人)とします。そのため、偏差値60未満が期待値深海魚となります。
上記の計算による一覧表です。1つ目は中学入学から高校進学の学力変化のシミュレーション結果です。

最上位の私立1中学では深海魚はほぼゼロですが、3年間の学力増減で偏差値60−64に11名(定員比5%)が出てきています。一方、私立3位の私立3中学では、下位合格者(入学時偏差値71)を中心に、偏差値60を割る生徒が出始めています。
続いて、高校進学から高校卒業の学力変化のシミュレーション結果です。

私立1高校でもついに期待値深海魚ラインを割る生徒が出てきます。定員の約5%が期待値深海魚(MARCH合格できない)となります。私立2高校と私立3高校では深海魚比率が1割を超えています。主に中学入学時の成績下位の生徒が占めています。
このようになるのは、中学入学時にその学校で相対的に成績が低い生徒が、中学3年間で勉強不足で成績が上がらず高校進学時に低い学力レベル(表1)に分布してしまっているためです。ただ、この段階はまだ相対的深海魚の範囲です。
ところが、そこから更に高校3年間で学力増減する際に、心機一転で学力増加する生徒もいるのですが、そうならずに相対的深海魚に留まると、周囲との学力格差が更に広がり、高校卒業時には期待値深海魚の閾値も割ってしまいます。
このようなメカニズムで、中高6年間に学力増減(今回は3年ごとの増減で標準偏差7点)する場合には、6年の時間経過があると、中学受験の最上位層でも深海魚になる層が一定数存在してしまうようです。言い換えると、ある時点の学力が直前の学力に依存する非独立な関係(例:高校卒業時の学力は高校進学時の学力に依存)の場合、6年間の時間経過とともに、私立中高一貫校のトップ校で深海魚が発生すると言えます。

3. 最後に
以上が中高一貫校の学力平均化と深海魚発生のメカニズムの考察となります。
このメカニズムのポイントは、「中高6年間で私立でも公立でも均等に学力増減が発生」と「ある時点の学力は直前の学力に依存(非独立)」という前提条件です。この前提が崩れると結論は大きく変わりますし、モデルに用いるパラメーターの値を変えても、結論に影響する可能性はあります。
ただ、もし上記の前提条件が正しいのだとすれば、これまでの考察を元にして、中学受験については以下の見解が導出できます。
単に学力面だけで見るなら、私立でも公立でも、中高6年間の学力増減で高校卒業時の学力は決まる
→大学受験のために、中学受験して「私立中高一貫校に入学すること自体」には、経済合理性がない逆に言えば、私立中高一貫校でも大学附属校や鉄緑会の指定校などでは、「私立中高一貫校に入学すること自体」に意味がある
→その分の入試難易度のプレミアムが乗るため、経済合理性はプレミアムの個人的評価に依存する中学受験であれ先取り学習(英語など)であれ、小学生のうちに学力レベルを上げておくことは、難関大学の合格にはメリットが大きい。
あくまで、一定の前提での仮想の都道府県でのシミュレーションからの考察と結論なので、その点はご留意ください。
