
【三角関数】正弦定理のつくりかた
三角比をやっていると登場する「正弦定理」と「余弦定理」。
丸暗記してしまえばそれでOK!
と教わるかもしれませんが、
それだとやっぱりもったいない。
ここでは、その背後にある原理に迫ってみたいと思います。
正弦定理
まずは正弦定理。$${\sin}$$に関する定理ですよね。
どんな定理だったかというと、
$$
\frac{a}{\sin A}= \frac{b}{\sin B}= \frac{c}{\sin C} = 2R
$$

ですよね。
これがなぜ成り立つのか?
ここで鍵となるのが、外接円の半径$${R}$$です。
例えば下のような感じに半径を描けますよね。

こんな図形を見ると、円周角と中心角の関係が使えそうです。
つまり
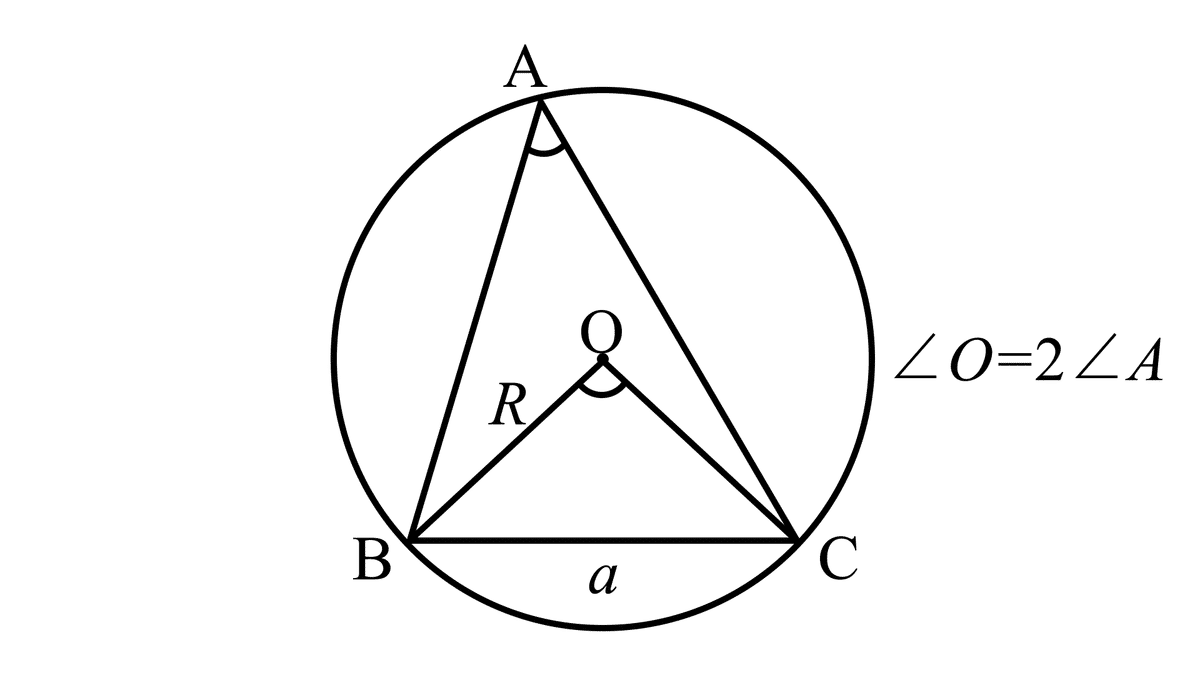
こうなるということ。
このあたりの関係をうまく使っていけば、
$${ \frac{a}{\sin A} = 2R }$$は導けそうな気がしませんか?
$${\angle \mathrm{O} = 2\angle \mathrm{A}}$$ってことは、
中心角を半分にすれば$${\angle \mathrm{A}}$$と一緒になりますよね。
その方が考えやすそう。
ということで、中心角を二等分する線を引くと

こんな感じになります!
$${\triangle \mathrm{OBC}}$$は二等辺三角形だから、
$${\angle \mathrm{O}}$$の二等分線がそのまま$${\mathrm{BC}}$$の垂直二等分線になるんです。
直角三角形ができたら、$${\sin}$$も考えやすいですよね。
$${\triangle \mathrm{OBM}}$$を拡大すると、こんな感じです↓

ということは、
$$
\def\arraystretch{3}
\begin{align*}
\sin A &= \frac{\frac{a}{2}}{R} \\
\sin A &= \frac{a}{2R} \\
2R &= \frac{a}{\sin A} \\
\end{align}
$$
となって、正弦定理が出てきました!
今回は$${A}$$について計算しましたが、
当然他の$${B}$$、$${C}$$についても同じことをすればよいから、
$${\frac{b}{\sin B}}$$も、$${\frac{c}{\sin C}}$$も、どちらも$${\frac{a}{\sin A}}$$と同様に$${2R}$$になるってわけですね。
ということで、めでたく
$$
{\frac{a}{\sin A}}={\frac{b}{\sin B}}={\frac{c}{\sin C}}=2R
$$
が導けました。
つまるところ、円周角の定理から自然に導くことができる性質ということなのです。
最後に宣伝を。
もし、勉強に対する悩みや不安を感じているなら、ぜひ私たちのオンライン個別指導サービス【Your Guide】をご検討ください。
あなたの目標達成に向けて、丁寧にサポートいたします。
勉強の楽しさを再発見し、自分のペースで確実に成長していける環境を提供します。
興味のある方は、ぜひお気軽にお問い合わせください。
あなたの未来への一歩を、私たちが全力でサポートします。
