
やさしい物理講座v47「慣性力と転向力(コリオリ力)の簡単な実験。Seeing is believing」
百聞は一見に如かず
「実際に体験した情報が一番強い」
「知之為知之、不知為不知、是知也」。
好奇心旺盛。
日常のレコード鑑賞をしながら、ビー玉を使い、その軌跡を観察する実験をした。
エルビスプレスリー、ローリングストーンズ、ビートルズなどのロックのリズムに乗りながらブログ作成している。
今回は、ロックのリズムに乗りながらのブログであるがご容赦頂きたい。
皇紀2682年7月19日
さいたま市桜区
理論物理研究者 田村 司
はじめに
実験の前に予備知識を掲載する。
運動の第1法則
「すべての物体は、外部から力を加えられない限り、静止している物体は静止状態を続け、運動している物体は等速直線運動を続ける。」これが慣性の法則と言われるものである。
運動の第2法則
運動の第1法則が成り立つ慣性系における、物体の運動状態の時間変化 ⊿t と物体 m に作用する力 ⊿vの関係を示す法則で、ニュートンの運動方程式と言われるものである。「速度が増加する、減速する、方向が変わる」などのことを加速度と表現する。時間が刻々と変わる力を記号Fで表すと式となる。余りむずかしく考えない。つまり、力Fは刻々と変化する状態であると考える。

ここで、 mは物体の質量、aは物体の加速度、Fは物体に加わる力とすると次の運動方程式が導かれる。

現代的記法に則して第2法則を記述するなら、ある短い時間 Δt に生じた物体の運動量の変化 Δp は、(現代物理学における意味での)力 F に比例する。

この両辺を時間 Δt で割り、運動量 p を時刻 t の関数と見なし Δt → 0 の極限をとれば、以下の微分方程式が得られる。この方程式はニュートンの運動方程式と呼ばれる。

さて、表題の実験と観察に着手する。

実験の目的
慣性力と転向力(コリオリ力)の考察
実験道具
レコードプレーヤー
LPレコード
ビー玉(直径1cm) 質量m
実験方法 1
摩擦・遠心力は考慮しない
レコードを時計周りに回転させる (右回転、角速度ω=1)
レコードの中心から外側にビー玉mをF₁の力で転がす
ビー玉mの運動の軌跡を確認する
実験の観察結果(ビー玉mの軌跡)
レコードの中心から徐々に右側へ曲線を描きながら移動する(図1)。
レコードは2秒間で1回転する(角速度ω=1 故に半径rに位置する速度はrで表される) このことからも時間tと位置に関係する事がわかる。

実験方法 2
レコードを右回りに回転させる
レコードの外側から中心にビー玉mを F₁の力で転がす
ビー玉mの軌跡を確認する
観察結果(ビー玉の軌跡)
レコードの外側から中心への徐々に右側へ曲がり移動する。(図2)
このことからも時間tと位置rに関係する事がわかる。

実験結果の考察
これらの現象を難しい言葉でいうと転向力(コリオリ力)と言う。
では何故起こるかというと要因は2つある。慣性力と円運動(又は球運動)が作り出した見かけ上の力(合力P)が働くとされる。
次の図で解説する。
レコードの中心から出たビー玉mはレコードの外側へ「F₁」の力で押し出される。その時(瞬間)のレコードの回転の力「F₂=0」であるので合力としての「p=F₁」で表される。しかし、ビー玉がレコードの中心から離れることにより「F₂=0」が「F₂=レコードの回転運動の接線の力」になることが分かる。
レコードの中心位置の力F₁は、θ=90°=1/2πからsinθ=1となり・・Psinθ=P=F₁ F₂=0(pcosθ=0) 偏向力Pはまだ発生しない
レコードの中心位置から離れた力F₂は、中心からのビー玉mの位置につまり半径rによってレコード盤のF₂の速度が半径rの接線の速度が決まる。それは、角速度ω(rad/s)からレコード盤は2秒間で1するので、角速度ω=πr回転 rが0→r (故に半径rに位置する速度はr・ωで表される)
つまり、ビー玉mの運動速度は r・ω で表される

動径方向の速度成分を持たないとき、すなわち原点からの距離が変化しないとき

しかし刻々とr(半径の距離)の数値が0からrへと変化していく
当然、合力pは時間と共に変化する。
ビー玉mが刻々と移動する合力pは時間変化⊿tの微分方程式で表すことが出来る。

dp/dt はビー玉mが持つ運動量 p の時間微分、F は物体にかかる力を表す。
その図が図1である。時間の変化dp/dt は半径の距離rとなって現れる。

F はビー玉mに働く力、p は物体の運動量、t は慣性系の時刻を表す。ニュートン力学において運動量は速度 v と慣性質量 m の積で表され、

また速度 v の時間微分は加速度 a であることから、物体の慣性質量は一定である場合について、次の関係が成り立つ。ビー玉mに働くFは次の要にも表示できる。

力Fを分解すると下図のようなF₁とF₂のベクトルで表される。そうするとPは合力として運動方向をも示す。今回の命題の転向力(コリオリ力)の発見に役立つことになる。pの方向性に注目しよう。

レコードの回転速度は角速度という概念で考えると分かり易い。
角速度はその名の通り、物が回転したときの速さを角度を使ってあらわした数値のこと指します。ちなみに、物が回転するときの速さを距離で表したものは周速度と言います。
角速度はラジアンという概念で考えることになる。一周を360で分割する方法とラジアンの違いは次の通りである。
円周は2πrで表される。これが360度である。
弧度法はradに半径をかけて弧の長さを求める【弧の長さ=円の半径xrad】
rad=弧の長さ÷円の半径 式を入れ替えると弧の長さ=円の半径xrad

「角度θ÷時間」ω = θ / t [rad/s]
ω:角速度(rad/秒)、θ:角度(rad)、t:時間(秒)
なので、レコード盤の角速度は2秒で一回転なのでωは2/2=1
F₂は半径rに比例しながら週速度も変化(0→r)
週速度はV = rω で表される。
V=m/秒、r=半径(m)、ω=角速度(rad/秒)
これがF₂=mVとなり同時に合力のPも変化する。
これにより時計周りのレコード円盤上ではビー玉mは中心から離れるほど、加速度(F₂)を増して、Pは右方向に刻々とずれて動くのである。
レコード盤が止まっているときにビー玉を観察した場合は中心から接線直角に向かって真っすぐに進む。しかしながらレコード盤が回転すると中心からの半径(r₀、r₁、r₂・・)の距離に比例して速度(ω・r)が増すことになる。接線の速度(週速度)はV = rωで表される。
F₂が大きくなるに従いPはF₂に近づく。つまり F₂=pcosθ θ→0になるとcosθ=1となり F₂=Pとなる。
当然、sinθ=0となり F₁=psinθであるからF₁の力の成分 F₁=0となり F₂=P だけが残る。
これが右に曲がる転向力(コリオリ力)の正体である。

上記の図2の解説、
図1の「F₁>0、F₂>0、」を「正」とするならば、図2は方向が「負」となるために
「F₁<0,F₂<0、」で表される。
レコード盤の接線から中心に向かうビー玉mは r(半径の距離)の数値がrからスタートして、⊿tごと⊿rが減少していく。V=(r・ω)となる。つまりF₂が最大値から と時間変化に従い F₂の分力が減少するようになる。F₂<0、F₂=F₂´ーF₂´´、F₂=F₂´´ーF₂´´´、F₂=F₂´´´ーF₂´´´´
rが減少すると週速度はV = rω も減少する。
F₁=一定(慣性力)、rが小さくなるに従い、週速度はV = rωも減少するので次の式が成り立つ。
F₂=F₂´ーF₂´´、 F₂´>F₂´´
F₂=F₂´´ーF₂´´´、 F₂´´>F₂´´´
F₂=F₂´´´ーF₂´´´´、 F₂´´´>F₂´´´´
・
・
・
図2のように、「F₂<0」で「負の方向である」ので、減速する加速度F₂は「負×負=正」となり方向が正に変わるり、合力pは次の「力の分解図」のようになる。
つまり「分力のF₁とF₂の合力p」となりPは右方向に曲がることになる。

失敗点
ビー玉を質点mに見立てたが、レコード盤上でビー玉が回転運動を起こす場面(現象)や、遠心力、など別な物理現象もみられたが、考察からは除外した。「F₁」の力加減によってビー玉が色々な軌跡をとることが分かったが、回転するレコード盤でのビー玉を質点と見立てた軌跡は理論的に納得できる結果となった。
バスの中での慣性力の例
次の図はバスの乗組員の慣性力の現象が分かる事例である。
慣性力=見かけの力とも言われている。
イメージ1はバスの発車のとき「ーF」が慣性力として衝撃を与える。
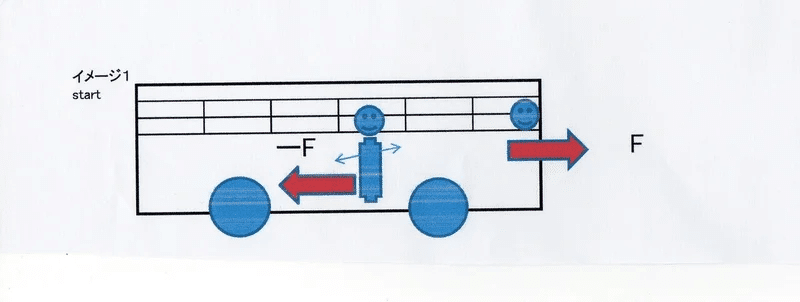
イメージ2はバスが急停車・又は衝突したとき「F」の慣性力として衝撃をうける。

蛇足
台風については以前のブログで分かり易く具体的それそれの緯度におけるの慣性力の差を計算しどのくらいの速度差が生じて右にずれるかを解説済みです。
やさしい物理講座v9「日常生活に見る慣性力(見かけの力)と転向力(コリオリ力)が作り出す台風の渦巻き」|tsukasa_tamura|note
簡単に言うと、台風が北半球で反時計回りの渦を巻くのは、風が低気圧中心に向かって進む際にコリオリの力を受け、進行方向に対し中心から右にずれた地点に到達するためである。
今回のレコード盤とビー玉の軌跡でお理解いただけると幸いです。なお、数式や解説に錯誤・誤謬・語弊がありましたらコメント頂けたら幸せです。微分方程式など使わずに解説しようと試みたが時間変化の考え方が必要であり、ちょっと使わせて頂きました。
See you later!
参考文献・参考資料
やさしい物理講座v9「日常生活に見る慣性力(見かけの力)と転向力(コリオリ力)が作り出す台風の渦巻き」|tsukasa_tamura|note
台風の渦巻きと慣性の法則|tsukasa_tamura|note
運動の第1法則 - Wikipedia
運動の第2法則 - Wikipedia
角速度ωの計算方法(公式)と角速度を使った周速度の求め方-円運動における角速度と周速度の関係とは - すみくにぼちぼち日記 (hatenablog.com)
この記事が気に入ったらチップで応援してみませんか?
