
ペンローズのグラフ記法による微分形式の公式の表現
PDF版は以下から。すべての情報についてPDF版が最新です。noteや他の媒体に比べて導出などを豊富に載せています。
https://lowtonevoice.github.io/math-phys-tech/penrose-notation/main.pdf
動画は2部構成にしました。
誤植の報告や質問などはnote最下部のコメント欄、Xのダイレクトメッセージ、GitHubのプルリクエストなどからお願いします。
前提知識・表記上の注意
前提知識
この記事では
微分形式
Lie微分
外微分
内部積
の知識を前提とします。加えて完全反対称Levi-Civitaテンソルの扱いに慣れておくと良いです。
また、「ペンローズのグラフ記法は初めましてです」という方は、まず以下の2つに目を通してください。
表記上の注意
基本的に添字を使う場合はEinsteinの縮約記法に従って表します。
微分記号$${∂_i}$$は括弧を使わない限り常に直後の量のみを微分するものとします。つまり$${∂_iA^jB^k=∂_i(A^j)B^k}$$です。
n次の対称群を$${\mathfrak{S}_n}$$とし、$${P\in\mathfrak{S}_n}$$の符号は$${\mathrm{sgn}(P)}$$で表します。k階の完全反対称Levi-Civitaテンソルは
$$
\epsilon_{\nu_1\nu_2\cdots\nu_k}^{\mu_1\mu_2\cdots\mu_k}\equiv\det\left(\begin{matrix}\delta_{\nu_1}^{\mu_1}&\cdots&\delta_{\nu_k}^{\mu_1}\\\vdots&\ddots&\vdots\\\delta_{\nu_1}^{\mu_k}&\cdots&\delta_{\nu_k}^{\mu_k}\end{matrix}\right)=\sum_{P\in\mathfrak{S}_n}\mathrm{sgn}(P)\delta_{\nu_1}^{P(\mu_1)}\cdots\delta_{\nu_k}^{P(\mu_k)}
$$
で定義します。
各演算の表式
微分形式 (k-form)
k-formを$${M}$$のベクトル場$${V_1=V_1^{\mu_1}∂_{\mu_1},\cdots,V_k=V_k^{\mu_k}∂_{\mu_k}}$$に作用させると、
$$
\begin{array}{rcl}\omega(V_1,\cdots,V_k)&=&\displaystyle\sum_{P\in\mathfrak{S}_k}\mathrm{sgn}(P)\omega_{\mu_1\cdots\mu_k}V^{\mu_{P(1)}}\cdots V^{\mu_{P(k)}}\\&=&\omega_{\mu_1\cdots\mu_k}\epsilon^{\mu_1\cdots\mu_k}_{\nu_1\cdots\nu_k}V^{\nu_1}\cdots V^{\nu_k}\end{array}
$$
と表せます。2段目の表式をもとに、Penroseのグラフ記法では以下のように表します。
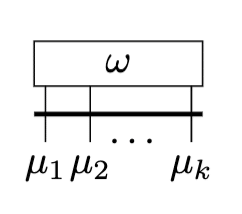
弱点として、$${M}$$上の点$${p}$$依存性を表すのには不向きです。結果、引き戻しやベクトルの押し出しなんかも不得手です。関連して、個人的には座標基底を図式に取り入れるのも好みではありません。反対称テンソルのせいで$${0}$$になりそうな見た目をしているので。
Lie微分
テンソルのLie微分はLeibnitz ruleによって以下の要領で展開できます。
$$
\begin{array}{l}\mathcal{L}_V(t_{\nu_1\cdots\nu_k}^{\mu_1\cdots\mu_l}\partial_{\mu_1}\otimes\cdots\partial_{\mu_l}\otimes d{x}^{\nu_1}\otimes\cdots\otimes d{x}^{\nu_k})\\=V^\lambda\partial_\lambda t_{\nu_1\cdots\nu_k}^{\mu_1\cdots\mu_l}\partial_{\mu_1}\otimes\cdots\otimes\partial_{\mu_l}\otimes d{x}^{\nu_1}\otimes\cdots\otimes d{x}^{\nu_k}\\\quad-t_{\nu_1\cdots\nu_k}^{\mu_1\cdots\mu_l}\partial_{\mu_1}V^\lambda\partial_\lambda\otimes\cdots\otimes\partial_{\mu_l}\otimes d{x}^{\nu_1}\otimes\cdots\otimes d{x}^{\nu_k}\\\quad-\cdots\\\quad-t_{\nu_1\cdots\nu_k}^{\mu_1\cdots\mu_l}\partial_{\mu_1}\otimes\cdots\otimes\partial_{\mu_l}V^\lambda\partial_\lambda\otimes d{x}^{\nu_1}\otimes\cdots\otimes d{x}^{\nu_k}\\\quad+t_{\nu_1\cdots\nu_k}^{\mu_1\cdots\mu_l}\partial_{\mu_1}\otimes\cdots\otimes\partial_{\mu_l}\otimes \partial_\lambda V^{\nu_1} d{x}^{\lambda}\otimes\cdots\otimes d{x}^{\nu_k}\\\quad+\cdots\\\quad+t_{\nu_1\cdots\nu_k}^{\mu_1\cdots\mu_l}\partial_{\mu_1}\otimes\cdots\otimes\partial_{\mu_l}\otimes d{x}^{\nu_1}\otimes\cdots\otimes\partial_\lambda V^{\nu_k} d{x}^{\lambda}\end{array}
$$
これをグラフ記法で表すと以下の通りです。

外積 (wedge product)
外積は太線をつなげるだけです。

実際、
$$
(\omega_{\mu_1\cdots\mu_k}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k})\wedge(\eta_{\nu_1\cdots\nu_l}dx^{\nu_1}\wedge\cdots\wedge dx^{\nu_l})=\omega_{\mu_1\cdots\mu_k}\eta_{\nu_1\cdots\nu_l}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}\wedge dx^{\nu_1}\wedge\cdots\wedge dx^{\nu_l}
$$
となります。
外微分
$$
d(\omega_{\mu_1\cdots}dx^{\mu_1}\wedge\cdots)=∂_\nu\omega_{\mu_1\cdots}dx^\nu\wedge dx^{\mu_1}\wedge\cdots
$$
を反映して以下のようにします。

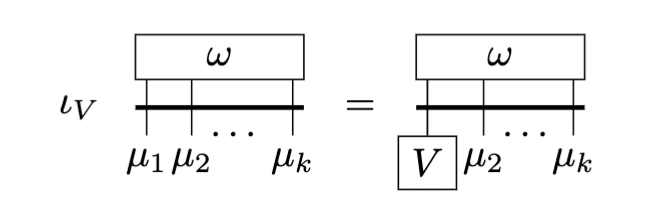
内部積
$$
\iota_V(\omega_{\mu_1\cdots\mu_k}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k})(V_1,\cdots,V_{k-1})=\sum_{s=1}^k\omega_{\mu_1\cdots\mu_s\cdots\mu_k}\epsilon^{\mu_1\cdots\mu_k}_{\nu_1\cdots\nu_k}V^{\nu_1}V_1^{\nu_2}\cdots V_{k-1}^{\nu_k}
$$
図で表すと下の通りです。
各種公式
Poincaréの補題
$$
d^2=0
$$
微分順序の交換と反対称性を使えば一発でわかります。

両辺を見比べると$${A=-A}$$の形になっているので、この値は$${0}$$に限られます。
内部積の別表現
内部積$${\iota_V\omega}$$を表す方法として、ベクトル$${V}$$で潰した$${\omega}$$の先頭の脚をLevi-Civitaテンソルから外す表し方があります。
$$
\iota_V\omega=k\omega_{\mu_1\cdots\mu_k}\epsilon^{\mu_2\cdots\mu_k}_{\mu_2'\cdots\mu_k'}V^{\mu_1'}dx^{\mu_2'}\otimes\cdots\otimes dx^{\mu_k'}
$$
Levi-Civitaテンソルの添字が$${\mu_2, \mu_2'}$$から始まることに注意してください。
これを証明するにはまず$${V}$$がつながった脚を反対称テンソルから外します。

$${\omega_{\mu_1\cdots\mu_k}}$$が添字に対して反対称であることに注意すると、1段目右辺にて正号がつくものは偶置換で、負号がつくものは奇置換で第1項に戻るので、各項全て同じ値となります。全部で$${k}$$項あるので2段目が得られます。
Cartanの公式
$$
d\iota_X+\iota_Xd=\mathcal{L}_X
$$
まずは左辺を書き出してみます。第 1 項の内部積は先ほどの別表現を使うのがいいでしょう。

右辺第1項はLeibnitz ruleによって分解します。
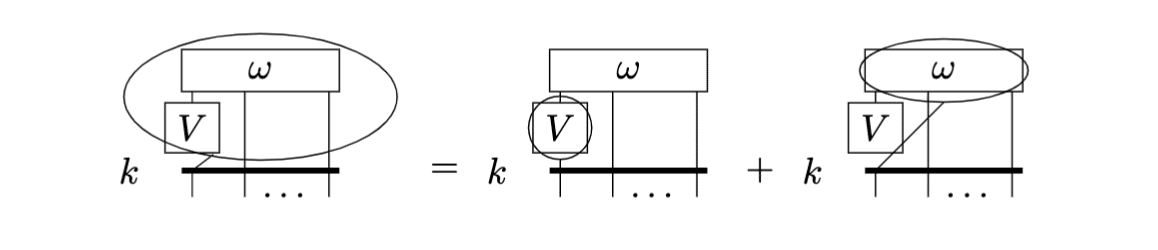
第2項は$${V}$$を反対称テンソルから外します。

従って元の式は以下の形になります。

さらに右辺第1項は$${\omega_{\mu_1\cdots\mu_k}}$$の添字に関する反対称性を使うことで以下のように展開できます。

これを元の式に戻すとk-formのLie微分に等しいことがわかります。よってCartanの公式が証明されました。
計量を含む多様体上の微分形式
ホッジスター
$${n}$$次元の計量が入った多様体について
$$
\ast\left(\frac{1}{k!}\omega_{\mu_1\cdots\mu_k}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}\right)=\frac{\sqrt{|g|}}{k!(n-k)!}g^{\mu_1\nu_1}\cdots g^{\mu_k\nu_k}\epsilon_{\mu_1\cdots\mu_k\mu_{k+1}\cdots\mu_n}dx^{\mu_{k+1}}\wedge\cdots\wedge dx^{\mu_n}
$$
なので、以下のように表せます。

余微分
$${k}$$-formへの作用は
$$
\delta=(-1)^{nk+n+1}\frac{g}{|g|}\ast d\ast
$$
で与えられ、これまでの図式から以下のように計算できます。

微分は$${\sqrt{|g|}}$$や$${\omega}$$に直接かかる$${g^{ij}}$$にも作用することに注意。
計量を含む多様体上の微分形式の公式
ホッジスターの2回作用
$${k}$$-form $${\omega}$$に対して、
$$
\ast\ast\omega=(-1)^{k(n-k)}\frac{g}{|g|}\omega
$$
です。

微分形式の外積
計量を含む$${n}$$次元多様体上の$${k}$$-form
$$
\xi=\frac{1}{k!}\xi_{\mu_1\cdots\mu_k}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}\\\eta=\frac{1}{k!}\eta_{\mu_1\cdots\mu_k}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}
$$
の外積は
$$
\left<\xi,\eta\right>=\xi\wedge\ast\eta=\frac{1}{k!}\xi_{\mu_1\cdots\mu_k}\eta^{\mu_1\cdots\mu_k}\sqrt{|g|}dx^1\wedge\cdots\wedge dx^n
$$
で与えられます。

