
統計学が最強の学問である 実践編①:中央値と平均値、因果関係を見るならどっちを使うべきか?
読書ノート(141日目)
明けましておめでとうございます🎍✨
2024年も引き続き、
どうぞよろしくお願いいたします。
さて、新年最初の読書ノートは…
昨年12月に宣言した目標の通り
「統計学が最強~」シリーズを読破する!
ということで、
今日からは「実践編」となります。
・序章:ビジネスと統計学を繋ぐために
・前著「統計学が最強の学問である」は
統計学の「入門の入門」について述べた本だった
・統計学の入門書の多くは、
確率論の説明、正規分布など確率分布の説明、
推定、検定、相関係数と回帰分析といった順番で
それぞれの概念を数学的に理解する、というのが一般的な内容
・第1章:統計学の実践は基本の見直しから始まる
・「平均」と「割合」の本質
・何かを集計するときには、
年齢や購入金額など連続値のときは「平均値」を、
性別や商品ジャンルなど非連続値のときは「割合」は使う
・統計学の実践は基本の見直しから始まる
・現状把握のための単純集計から、
分析による因果関係の洞察に踏み出すにあたり
まず身につけるべき知恵は3つ
(1)平均値や割合など統計指標の本質的な意味の理解
(2)「データを点ではなく幅で捉える」という考え方
(3)「何の値を何ごとに集計すべきか」という考え方
・因果関係の「洞察」には中央値よりも平均値を
・「現状把握」の統計学では平均値に加え、
中央値や最頻値と呼ばれる代表値がある
・因果関係の洞察を行う関心は多くの場合
「何かの要因を変えれば結果の値の総量がどうなるか」
であり、平均値はその答えを与えてくれるが中央値はその答えを与えない
・例えば、駄菓子屋さんに9人の顧客がいて、
8人は1回あたり300円、1人だけ2100円の顧客がいる場合、
仮に当たりくじを使って客単価を伸ばそうとした際に、
2100円の顧客の客単価だけが3000円に上昇すると
平均値は変化するが、中央値では変化がない結果となる。
・中央値を使った場合、当たりくじの有無で「変化なし」=「効果なし」
ということになってしまう
・標準偏差が示す「たいていのデータの範囲」
・現状把握に便利な四分位点
・平均客単価が3千円とだけ言われても、
「ほとんどの人が3千円前後使う」のか
「1000円しか使わない人も1万円使う人もいる」のかは分からない
・四分位点とは25%点、75%点、中央値を合わせたもので
データの幅を示すために用いる
・「チェビシェフの不等式」
ロシア人数学者のチェビシェフにより、
データのバラつきがどのようなものであれ、
平均値±2SD(標準偏差の2倍)までの範囲に
必ず全体の4分の3以上のデータが存在することを証明
さて、今日からは
「統計学が最強~」シリーズ全4冊のうち
2冊目に突入しました。
当初の予定からはやや遅れ気味ですが
今日はこの後で初詣など外出もあるので
明日から読書ペースを挽回する予定です!
さて今回は、数ある代表値の中でも
因果関係を見つけたいなら
中央値よりも平均値を使うべき。
でも平均値だけではデータの幅が
分からないから、四分位点も使おう!
という内容でした。
本書ではグラフ付きで
標準偏差から因果関係を洞察する
という内容が説明されており、
僕自身も重要だと感じたのですが
紙の本を写真で撮影しても
あまり綺麗にアップロードできず…
ということで、同じような内容が
こちらのサイトに記載されていたので、
お借りして説明すると…
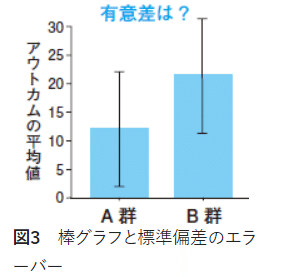
以下の棒グラフは、
A群とB群の平均値を比較したもので、
B群の平均値の方がA群よりも
高いことは分かりますが、
この差がたまたま偶然なのか、
そうでなく有意差なのかは
このグラフだけでは分からない…

そこで、標準偏差の出番!
ということで、
標準偏差をグラフ上に表すと
以下のようになりました。
一見すると、ヒゲの部分が
A群とB群で重なっている面積が
大きいので、平均値の差は
なんだか偶然生じているようにも
見えますが…
ここで平均値の差を検定する
T検定を実施したところ
偶然性を示すp値は0.003だったようで
(有意差がない可能性がある確率は0.3%)
つまり
たまたま偶然では起きない差がある
と統計的に検定ができた。
ということになります。
もしA群とB群がランダムに選ばれていて
何かの施策や処置がB群だけにされた。
という条件があって、この結果が出れば
その施策や処置は効果があっただろう。
と言え、因果関係の洞察ができます。
ExcelでもT検定はt.test関数で
簡単にp値を計算することができるので、
シンプルながら強力な武器ですね…!
ということで今日はこの辺で!
それでは皆さんも
良い元日をお過ごしくださいー!
そして、皆さんにとっても
僕にとっても素敵な2024年にしましょう!✨
それではまたー!😉
