高知県Ｂ日程｜公立高校入試確率問題2024

　１から６までの目が出る２つのさいころＡ，Ｂを同時に投げるとき，さいころＡの出た目の数を$${a}$$，さいころＢの出た目の数を$${b}$$とする。このとき，$${a+b-1}$$が素数となる確率を求めなさい。ただし，さいころはどの目が出ることも同様に確からしいとする。

分類：１１　さいころ２つ－代入（その１）

さいころ２つなので表

　さいころ２つなので，まずは表を書いて、各マスに$${a+b-1}$$を計算して入れてしまいましょう。

　そのうち素数ができるのは

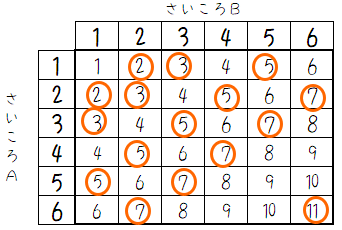
１６通り（１が素数でないこと、２を数え忘れないこと！）。ですから、その確率を求めると$${\dfrac{16}{36}=\dfrac{4}{9}}$$となります。

（別解）素数から迎えに行く

　このnoteでは，とにかく確実にもれなくダブりなく列挙できる表をお勧めしていますが，慣れてきてもれダブりを心配しないでスピードアップするなら，もちろん，素数という条件の方から迎えに行くアプローチもあります。
　$${a+b-1}$$の範囲は1から11ですから、この範囲の素数について、（$${a，b}$$）の組を考えます。すると、
２　（1,2），（2,1）２通り
３　（1,3），（2,2），（3,1）３通り
５　（1,5），（2,4），（3,3），（4,2），（5,1）５通り
７　（2,6），（3,5），（4,4），（5,3），（6,2）５通り
１１　（6,6）１通り
で、合わせて１６通り。

　どちらにしても，やってみて列挙しないとわからない、中学確率問題の典型問題ですね。

答

$${\bm{\dfrac{4}{9}}}$$