
鳥取県|公立高校入試確率問題2024
3枚の硬貨を同時に投げるとき,少なくとも1枚は表となる確率を求めなさい。
ただし,硬貨を投げるときの表,裏の出かたは,同様に確からしいものとする。
硬貨に区別をつけて、樹形図
問題文には、3枚の硬貨がどういう種類のものかは書いていません。3枚が見た目全く同じもので、見分けがつかないものかもしれません。確率を計算するためには同様に確からしいことがらを並べる必要がありますが、見分けのつかない硬貨を同時に投げてしまうと、「同様に確からしい」ことがらを区別することができなくなります。
そのためには、3人で1枚ずつ分担することができますので、1つひとつの硬貨は区別して、起こりうる場合を並べて考えます。
Aさん、Bさん、Cさんにそれぞれ1枚ずつ硬貨を投げるのを分担してもらうことにすると、区別できる偶然は3つ起こりますので、次のように樹形図をかいて考えることができます。起こりうるすべての場合の数は8通り。
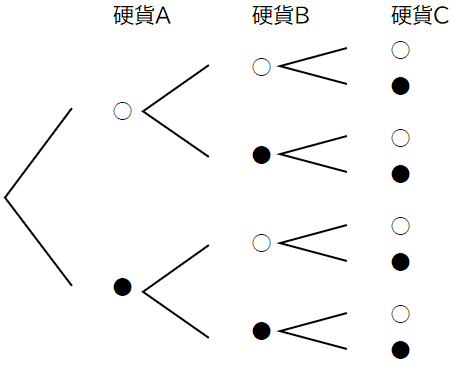
当てはまる条件は「少なくとも1」なので,じゃない方を考えた方がよいというサインです。「少なくとも1枚は表となる」じゃないというのは,「3枚とも裏」ですから,1通りしかありません。
求める確率は,$${1-\dfrac{1}{8}=\bm{\dfrac{7}{8}}}$$。
答
$${\bm{\dfrac{7}{8}}}$$
