岐阜県｜公立高校入試確率問題2024

　右の図のような正三角形ＡＢＣがあり，点Ｐは頂点Ａの位置にある。また。０から４までの数字が１つずつ書かれた５枚のカード[０][１][２][３][４]が，袋の中に入っている。
　次の操作を２回行う。

【操作】
　袋からカードを１枚取り出し，そのカードに書かれた数字の回数だけ，Ｐを正三角形の頂点から頂点へ左回りに移動させる。Ｐを移動させた後，取り出したカードを袋に戻す。

　例えば，１回目に[２]のカードを，２回目に[０]のカードを取り出したとき，１回目の操作後にＰは頂点Ｃにあり，２回目の操作後もＰは頂点Ｃにある。
　次の（１）～（３）の問いに答えなさい。
（１）　１回目の操作後にＰが頂点Ａにある確率を求めなさい。
（２）　１回目の操作後にＰが頂点Ａにあり，２回目の操作後もＰが頂点Ａにある確率を求めなさい。
（３）　２回目の操作後にＰが頂点Ａにある確率を求めなさい。

分類：応用❷（他のものを動かす、循環型）

（１）偶然が１回だけ起こるときの確率

　起こりうることがらは，例えば[１]のカードをひくことを［１］と表せば，［０］，［１］，［２］，［３］，［４］，［５］の５通りで，どのことがらが起こることも同様に確からしいですね。
　１回目の操作後にＰが頂点Ａにあるのは，その５通りのうち，［０］，［３］が起こったときの２通りですので，その確率は$${\dfrac{2}{5}}$$ということになります。

（２）偶然が２回起こるときの確率

　さいころ２回なので表をかいてしまうのがよいですね。

　１回目で点Ｐがどこの位置にあるのかも書き込んでしまった方がよいでしょう。

　起こりうるすべての場合の数は２５通りです。それで，ここでは１回目にＡの位置にあるところだけ考えればよいので，

　すると，２回目の操作でもＡの位置のある場合は

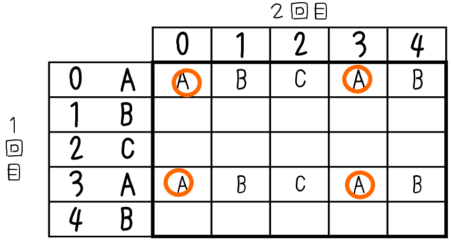
この４通りなので，その確率は$${\dfrac{4}{25}}$$と求められます。

（３）さっきの表を使ってさらに

　先ほどの表で，埋めなかったところも埋めて考えてみることにしましょう。

　すると，１回目の操作にかかわらず２回目でAの位置にあるのは

８通り，ということになりますので，求める確率は$${\dfrac{8}{25}}$$です。

答

（１）$${\bm{\dfrac{2}{5}}}$$　　　（２）$${\bm{\dfrac{4}{25}}}$$　　　（３）$${\bm{\dfrac{8}{25}}}$$

問題を解いた後に・・・

　実は，出たカードの数は，点Ｐの移動回数ですから，その和を求めて，

それを３でわった余りを考えれば，
　　　余り０（0，3，6）　→　Ａ
　　　余り１（1，4，7）　→　Ｂ
　　　余り２（2，5，8）　→　Ｃ
の位置にいることがわかります。三角形ぐらいの単純さなら，表をかいて力業でも大丈夫だと思いますが，ちょっと上を目指す人は，この「割り算のあまり」の考え方にも慣れておくとよいでしょう。