（追記有り）＜アーベルの証明③＞５次置換のうち、遇置換を３次巡回置換で表す

　クリームソーダを飲み終えた森田君は、「それでは再開します」とすぐにホワイトボードの前に立った。一つ一つ確認するように進めていくのが小学５年生の森田君のスタイル。とても丁寧に進めていくので竹村先生の出番はほとんどない。
　「では先ほどの授業の続きです。以前に６通りある３次置換をすべて互換で表し、遇置換と奇置換に分類しました（本シリーズ (6)）。先ほどは１２０通りある５次置換をすべて互換で表し、遇置換と奇置換に分類しました（本シリーズ (15)）。３次置換や５次置換で対称性を保つ式は、あらゆる置換を作用させても変化しない対称式です。その対称式の集合に、３次置換では $${X_3}$$、５次置換では $${X_5}$$ という差積を添加することによって、対称性を保つ置換を遇置換まで絞り込みました。いわば完全なる対称性（対称式）を、遇置換シンメトリーまで破壊する（崩す）ことができたわけです（本シリーズ (14)）。

$$
\begin{gather*}
{\bf ３次置換（対称式）}\\
6  通り\\[4pt]
\hspace{63pt}\downarrow  \Leftarrow 差積 X_3 の添加\\[6pt]
{\bf 遇置換シンメトリー}\\
\hspace{4pt}3  通り
\end{gather*}
\hspace{15pt}
\begin{gather*}
{\bf ５次置換（対称式）}\\
\,120  通り\\[4pt]
\hspace{63pt}\downarrow  \Leftarrow 差積 X_5 の添加\\[6pt]
{\bf 遇置換シンメトリー}\\
\hspace{4pt}60  通り\\[2pt]
\end{gather*}
$$

　次のステップとして、以前先生から次の性質を教えてもらいました。
　『すべての遇置換は３次巡回置換で表すことができる』
３次置換のうち３通りの遇置換は、すべて３次巡回置換で表すことができます（本シリーズ (14)）（注１）。そこでここからは、５次置換のうち６０通りある遇置換も、すべて３次巡回置換で表してみようと思います。３次方程式の解の公式では、対称性を保つ置換を恒等置換にまで絞り込むことによって解の公式が導出できました（本シリーズ (12)、(13)）。その導出過程と同じ経路をたどることで、５次以上の方程式では矛盾が生じ、解の公式が存在すると仮定することでの背理法によって、解の公式が存在しないことが証明できそうです」

$$
\begin{gather*}
{\bf ３次置換（対称式）}\\
\,6  通り\\[4pt]
\hspace{63pt}\downarrow  \Leftarrow 差積 X_3 の添加\\[6pt]
{\bf 遇置換シンメトリー}\\
\hspace{4pt}3  通り\\[4pt]
\hspace{63pt}\downarrow  \Leftarrow A の添加\\[6pt]
{\bf 恒等置換}\\
\,\,\,1  通り\\
\hspace{2pt}\downarrow\\
{\bf 解の公式が存在する}\\[-48pt]
\end{gather*}
\hspace{0pt}
\begin{gather*}
{\bf ５次方程式に解の公式}\\
{\bf が存在すると仮定する}\hspace{8pt}\\
\hspace{2pt}\downarrow\\
{\bf ５次置換（対称式）}\\
\,120  通り\\[4pt]
\hspace{63pt}\downarrow  \Leftarrow 差積 X_3 の添加\\[6pt]
{\bf 遇置換シンメトリー}\\
\hspace{4pt}60  通り\\[4pt]
\hspace{63pt}\downarrow  \Leftarrow ？ の添加\\
\hspace{2pt}\vdots\\
{\bf 矛盾}\\
\hspace{2pt}\downarrow\\
{\bf 解の公式が存在しない（背理法）}
\end{gather*}
$$

「なるほど・・・」と竹村は小さくつぶやく。
　森田君はマーカーを手に取った。
「では遇置換を３次巡回置換で表すにあたって、まずは２つの公式を提示していきます。

1. ３次巡回置換を共通の文字を含む互換の積で表す（復習）

　まずは復習として、次の式を確認します。休憩前、注意３-２『３次巡回置換を互換の積で表す方法』でやりました。

$$
\begin{align*}
(\underline{x_1}     x_2     x_3)=(\underline{x_1}     x_2)(\underline{x_1}     x_3)
\end{align*}
$$

これは３次巡回置換を、互換の積で表す公式とみることができます。３次巡回置換 $${(x_1     x_2     x_3)}$$ は、$${x_1}$$ と $${x_2}$$ との互換 $${(x_1     x_2)}$$ と、$${x_1}$$ と $${x_3}$$ との互換 $${(x_1     x_3)}$$ の積で表せる、という公式です。最初の文字（下線部）が常に先頭になるよう変換します。なお、互換は前から（左から）作用させると定義したので
　$${(x_1     x_2)(x_1     x_3)}$$
は先に $${(x_1     x_2)}$$ を作用させてから、次に $${(x_1     x_3)}$$ を作用さます。
　他に例を上げると

$$
\begin{align*}
(\underline{x_1}     x_3     x_4)&=(\underline{x_1}     x_3)(\underline{x_1}     x_4)\\
(\underline{x_1}     x_4     x_3)&=(\underline{x_1}     x_4)(\underline{x_1}     x_3)\\
(\underline{x_2}     x_4     x_5)&=(\underline{x_2}     x_4)(\underline{x_2}     x_5)\\
(\underline{x_3}     x_5     x_4)&=(\underline{x_3}     x_5)(\underline{x_3}     x_4)\\
\end{align*}
$$

先頭にある下線部の文字を、互換の先頭で固定するのがポイントです。
　これは、記号を使って次のように図式化することが可能です。

$$
\begin{align*}
(〇     ♠     ♣)=(〇     ♠)(〇     ♣)
\end{align*}
$$

先頭の〇を固定して、♠との互換、♣との互換と順に並べていきます。
　この公式を左右逆にすると、共通の文字を含む互換の積を３次巡回置換に変換する公式としてみることもできます。ではそれについてみていきます。

2. 共通の文字を含む互換の積を３次巡回置換で表す。

　先ほどの

$$
\begin{align*}
(\underline{x_1}     x_2     x_3)=(\underline{x_1}     x_2)(\underline{x_1}     x_3)
\end{align*}
$$

について、両辺を逆にしてみます。

$$
\begin{align*}
(\underline{x_1}     x_2)(\underline{x_1}     x_3)=(\underline{x_1}     x_2     x_3)
\end{align*}
$$

これは、共通の文字を含む互換の積を３次巡回置換に変換する公式としてみることができます。つまり、各々の互換の最初にある $${x_1}$$ を先頭に $${x_2}$$,  $${x_3}$$ と順に並べていきます。これを図式化すると次のように表せます。

$$
\begin{align*}
(〇     ♠)(〇     ♣)=(〇     ♠     ♣)　\cdots（公式１）
\end{align*}
$$

つまり$${〇}$$を先頭にして、赤矢印の順に文字を並べていきます。

この公式を使った具体例をみていきます。

$$
\begin{align*}
(\underline{x_1}     x_3)(\underline{x_1}     x_4)&=(\underline{x_1}     x_3     x_4)\\
(\underline{x_1}     x_4)(\underline{x_1}     x_3)&=(\underline{x_1}     x_4     x_3)\\
(\underline{x_2}     x_4)(\underline{x_2}     x_5)&=(\underline{x_2}     x_4     x_5)\\
(\underline{x_3}     x_5)(\underline{x_3}     x_4)&=(\underline{x_3}     x_5     x_4)
\end{align*}
$$

最初の下線部の文字を、３次巡回置換の先頭で固定するのがポイントです。
　なお $${(x_4     x_1)=(x_1     x_4)}$$ であることから、文字の順番が違っても、並べ替えることによって次のように（公式１）が使えるようになります。

$$
\begin{align*}
(\underline{x_1}     x_3)(x_4     \underline{x_1})&=(\underline{x_1}     x_3)(\underline{x_1}     x_4)\\
&=(\underline{x_1}     x_3     x_4)
\end{align*}
$$

　これで、共通の文字を含む互換の積を３次巡回置換で表す方法がわかりました。次は共通の文字の無い、互いに独立した互換の積を３次巡回置換で表す方法を考えます。

3. 共通の文字を含まない互換の積を３次巡回置換で表す。

　共通の文字を含まない互換の積とは、例えば次のような式です。

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)
\end{align*}
$$

最初の互換 $${(x_1     x_2)}$$ と次の互換 $${(x_3     x_4)}$$ には共通の文字がありません。これを３次巡回置換で表すには、間に恒等置換である
　$${I=(x_2     x_3)(x_2     x_3)}$$
をはさみ、次のようにします。

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)&=(x_1     x_2)  I  (x_3     x_4)\\
&=(x_1     x_2)\underset{恒等置換を間にはさむ}{\underline{(x_2     x_3)(x_2     x_3)}}(x_3     x_4)
\end{align*}
$$

$${(x_2     x_3)(x_2     x_3)}$$ は、$${x_2}$$ と $${x_3}$$ を入れ替えた後、もう一度 $${x_2}$$ と $${x_3}$$ を入れ替えるので、作用させても変化しない恒等置換 $${I}$$ となります。実際、文字列
　$${x_1,  x_2,  x_3,  x_4,  x_5}$$
に $${(x_2     x_3)(x_2     x_3)}$$ を作用させると

$$
\begin{align*}
x_1       x_2       &x_3       x_4       x_5\\
&\Downarrow　(x_2     x_3)  を作用\\
x_1       x_3       &x_2       x_4       x_5\\
&\Downarrow　(x_2     x_3)  を作用\\
x_1       x_2       &x_3       x_4       x_5　\leftarrow 変化しない
\end{align*}
$$

より何も変化しないので、$${(x_2     x_3)(x_2     x_3)}$$ は恒等置換 $${I}$$ です。恒等置換は途中にはさんでも、もとの置換と変化しません。ただしはさみ方として、次のように $${x_2}$$ と $${x_3}$$ がつながるようにはさみ込みます。

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)=(x_1     \underline{x_2})(\underline{x_2}     x_3)(x_2     \underline{\underline{x_3}})(\underline{\underline{x_3}}     x_4)
\end{align*}
$$

一重線部 $${x_2}$$ と、二重線部 $${x_3}$$ がつながるように恒等置換
　$${I=(x_2     x_3)(x_2     x_3)}$$
をはさみ込むわけです。次に前２つと、後ろ２つをセットにして、２つの積に分けます。

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)=\underset{この２つをセット}{\underline{(x_1     x_2)(x_2     x_3)}}\,\underset{この２つをセット}{\underline{\underline{(x_2     x_3)(x_3     x_4)}}}
\end{align*}
$$

次に、前２つの先頭を $${x_2}$$ に、後ろ２つの先頭を $${x_3}$$ でそろえて

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)=\underset{先頭の文字をそろえる}{\underline{(x_2     x_1)(x_2     x_3)}}\,\underset{先頭の文字をそろえる}{\underline{\underline{(x_3     x_2)(x_3     x_4)}}}
\end{align*}
$$

ここで、先にやった（公式１）

を用いると、最初の互換の積は
　$${(\underline{x_2}     x_1)(\underline{x_2}     x_3)=(\underline{x_2}     x_1     x_3)}$$
後ろの互換の積は
　$${(\underline{x_3}     x_2)(\underline{x_3}     x_4)=(\underline{x_3}    x_2     x_4)}$$
とそれぞれ３次巡回置換で表せるので

$$
\begin{align*}
(x_2     x_3)(x_2     x_3)=\underset{公式１利用}{\underline{(x_2     x_1     x_3)}}\,\underset{公式１利用}{\underline{\underline{(x_3     x_2     x_4)}}}
\end{align*}
$$

さらに、先頭の文字の添え字が最小になるように文字を並べ替えると　
　$${(x_2     \underline{x_1}     x_3)=(\underline{x_1}     x_3     x_2)}$$
　$${(x_3     \underline{x_2}     x_4)=(\underline{x_2}     x_4     x_3)}$$
となるので

$$
\begin{align*}
(x_2     x_3)(x_2     x_3)=\underline{(x_1     x_3     x_2)}\,\underline{\underline{(x_2     x_4     x_3)}}
\end{align*}
$$

となり、これで完成となります。もう一度まとめますと

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)&=(x_1     x_2)\underset{恒等置換を間に挟む}{\underline{(x_2     x_3)(x_2     x_3)}}(x_3     x_4)\\
&=\underset{前の２つをセット}{\underline{(x_1     x_2)(x_2     x_3)}}\,\underset{後ろの２つをセット}{\underline{\underline{(x_2     x_3)(x_3     x_4)}}}\\
&=\underset{先頭の文字をそろえる}{\underline{(x_2     x_1)(x_2     x_3)}}\,\underset{先頭の文字をそろえる}{\underline{\underline{(x_3     x_2)(x_3     x_4)}}}\\
&=\underset{公式１利用}{\underline{(x_2     x_1     x_3)}}\,\underset{公式１利用}{\underline{\underline{(x_3     x_2     x_4)}}}\\
&=\underset{並び替え}{\underline{(x_1     x_3     x_2)}}\,\underset{並び替え}{\underline{\underline{(x_2     x_4     x_3)}}}
\end{align*}
$$

より

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)&=(x_1     x_3     x_2)(x_2     x_4     x_3)
\end{align*}
$$

と、３次巡回置換の積で表すことができました。具体的に等しくなることを確認します。文字列 $${x_1,  x_2,  x_3,  x_4,  x_5}$$ に左辺 $${(x_1     x_2)(x_3     x_4)}$$ を作用させると

$$
\begin{align*}
x_1       x_2       &x_3       x_4       x_5\\
&\Downarrow　(x_1     x_2)  を作用\\
x_2       x_1       &x_3       x_4       x_5\\
&\Downarrow　(x_3     x_4)  を作用\\
x_2       x_1       &x_4       x_3       x_5     \cdots  (*1)
\end{align*}
$$

一方、右辺 $${(x_1     x_3     x_2)(x_2     x_4     x_3)}$$ を作用させると

$$
\begin{align*}
x_1       x_2       &x_3       x_4       x_5\\
&\Downarrow　(x_1     x_3     x_2)  を作用\\
x_3       x_1       &x_2       x_4       x_5\\
&\Downarrow　(x_2     x_4     x_3)  を作用\\
x_2       x_1       &x_4       x_3       x_5     \cdots  (*2)
\end{align*}
$$

より、$${(*1)}$$ と $${(*2)}$$ は同じ結果となります。この変換

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)&=(x_1     x_3     x_2)(x_2     x_4     x_3)
\end{align*}
$$

は、次のような形式で公式化してもいいでしょう。

$$
\begin{align*}
(〇     ♠)(△     ♣)&=(〇     △     ♠)(♠     ♣     △)　\cdots（公式２）
\end{align*}
$$

つまり、赤矢印、青矢印の順に文字を拾っていきます。

例を上げますと

（例）

$$
\begin{align*}
(x_1     x_3)(x_4     x_5)&=(x_1     x_4     x_3)(x_3     x_5     x_4)\\
(x_2     x_5)(x_3     x_4)&=(x_2     x_3     x_5)(x_5     x_4     x_3)\\
&=(x_2     x_3     x_5)\underline{(x_3     x_5     x_4)}
\end{align*}
$$

なお下線部は、先頭の文字の添え字が最小になるように並べ替えています。

4. ５次置換を遇置換と奇置換に分類（復習）

　さて休憩前の授業では５次置換すべてを互換の積で表し、遇置換と奇置換に分類しました。偶数個の互換の積が遇置換、奇数個の互換の積が奇置換です。再び確認します。

(case1)　動かない文字が５つの場合　$${1}$$ 通り　遇置換
例　恒等置換 $${I=(x_1     x_2)(x_1     x_2)}$$
(case2)　動かない文字が３つの場合　$${10}$$ 通り　奇置換
例　互換 $${(x_1     x_2)}$$
(case3)　動かない文字が２つの場合　$${20}$$ 通り　遇置換
例　３次巡回置換 $${(x_1     x_2     x_3)=(x_1     x_2)(x_1     x_3)}$$
　　これは共通の文字が１つある２つの互換の積とみることもできる。
(case4)　動かない文字が１つの場合
　(case4-1)     共通の文字のない２つの互換の積　$${15}$$ 通り　遇置換
例　$${(x_1     x_2)(x_3     x_4)}$$
　(case4-2)　４次巡回置換　$${30}$$ 通り　奇置換
例　$${(x_1     x_2     x_3     x_4)=(x_1     x_2)(x_1     x_3)(x_1     x_4)}$$
(case5)　動かない文字が０の場合
　(case5-1)　互いに共通の文字のない、１つの互換と３次巡回置換との積　$${20}$$ 通り　奇置換
例　$${(x_1     x_2)(x_3     x_4     x_5)=(x_1     x_2)(x_3     x_4)(x_3     x_5)}$$
　(case5-2)　５次巡回置換　$${24}$$ 通り
例　$${(x_1     x_2     x_3     x_4     x_5)=(x_1     x_2)(x_1     x_3)(x_1     x_4)(x_1     x_5)}$$　遇置換

　全部で何通りあるかを確認すると
　(case1)+(case2)+(case3)+(case4-1)+(case4-2)+(case5-1)+(case5-2)
$${＝1+10+20+15+30+20+24}$$
$${=120}$$ 通り
となります。そのうち遇置換は
　(case1)+(case3)+(case4-1)+(case5-2)
$${＝1+20+15+24}$$
$${=60}$$ 通り
奇置換は
　(case2)+(case4-2)+(case5-1)
$${＝10+30+20}$$
$${=60}$$ 通り
となり、遇置換と奇置換の数はちょうど半分ずつの $${60}$$ 通りになります。

5. 60通りの遇置換を３次巡回置換で表す。

　ではこの $${60}$$ 通り遇置換について、それぞれのケースごとに３次巡回置換、または３次巡回置換の積で表していきます。

(case1)　動かない文字が５つの場合

　この場合は何も変化させない恒等置換 $${I}$$ でした。３次巡回置換は同じ置換を３回繰り返せば元に戻るので、例えば

$$
\begin{align*}
I=(x_1     x_2     x_3)(x_1     x_2     x_3)(x_1     x_2     x_3)
\end{align*}
$$

と表すことによって、恒等置換を３次巡回置換の積で表すことができます。$${(x_1     x_2     x_3)}$$ は
　$${x_1 \rightarrow x_2 \rightarrow x_3 \rightarrow x_1}$$
と、$${x_1}$$ を $${x_2}$$ に、 $${x_2}$$ を $${x_3}$$ に、$${x_3}$$ を $${x_1}$$ に巡回的に入れ替える置換です。この置換を３回連続作用させると元に戻ります。実際、文字列
　$${x_1       x_2       x_3       x_4       x_5}$$
に $${(x_1     x_2     x_3)(x_1     x_2     x_3)(x_1     x_2     x_3)}$$ を作用させると

$$
\begin{align*}
x_1       x_2       &x_3       x_4       x_5\\
&\Downarrow　(x_1     x_2     x_3)  を作用\\
x_2       x_3       &x_1       x_4       x_5\\
&\Downarrow　(x_1     x_2     x_3)  を作用\\
x_3       x_1       &x_2       x_4       x_5\\
&\Downarrow　(x_1     x_2     x_3)  を作用\\
x_1       x_2       &x_3       x_4       x_5　\Leftarrow 変化しない
\end{align*}
$$

となり、何も変化しません。よって、恒等置換 $${I}$$ は

$$
\begin{align*}
I=(x_1     x_2     x_3)(x_1     x_2     x_3)(x_1     x_2     x_3)
\end{align*}
$$

と３次巡回置換の積で表すことができました。

(case3)　動かない文字が２つの場合

　この場合は３次巡回置換そのもので、次のように①から⑮の $${15}$$ 通りの置換がありました。

（再掲）

$$
\begin{align*}
&(x_1     〇     〇)  型\\
&①       (x_1     x_2     x_3)=(x_1     x_2)(x_1     x_3)\\
&②       (x_1     x_2     x_4)=(x_1     x_2)(x_1     x_4)\\
&③       (x_1     x_2     x_5)=(x_1     x_2)(x_1     x_5)\\
&④       (x_1     x_3     x_2)=(x_1     x_3)(x_1     x_2)\\
&⑤       (x_1     x_3     x_4)=(x_1     x_3)(x_1     x_4)\\
&⑥       (x_1     x_3     x_5)=(x_1     x_3)(x_1     x_5)\\
&⑦       (x_1     x_4     x_2)=(x_1     x_4)(x_1     x_2)\\
&⑧       (x_1     x_4     x_3)=(x_1     x_4)(x_1     x_3)\\
&⑨       (x_1     x_4     x_5)=(x_1     x_4)(x_1     x_5)\\
&⑩       (x_1     x_5     x_2)=(x_1     x_5)(x_1     x_2)\\
&⑪       (x_1     x_5     x_3)=(x_1     x_5)(x_1     x_3)\\
&⑫       (x_1     x_5     x_4)=(x_1     x_5)(x_1     x_4)\\[5pt]
&(x_2     〇     〇)  型\\
&⑬       (x_2     x_3     x_4)=(x_2     x_3)(x_2     x_4)\\
&⑭       (x_2     x_3     x_5)=(x_2     x_3)(x_2     x_5)\\
&⑮       (x_2     x_4     x_3)=(x_2     x_4)(x_2     x_3)\\
&⑯       (x_2     x_4     x_5)=(x_2     x_4)(x_2     x_5)\\
&⑰       (x_2     x_5     x_3)=(x_2     x_5)(x_2     x_3)\\
&⑱       (x_2     x_5     x_4)=(x_2     x_5)(x_2     x_4)\\[5pt]
&(x_3     〇     〇)  型\\
&⑲       (x_3     x_4     x_5)=(x_3     x_4)(x_3     x_5)\\
&⑳       (x_3     x_5     x_4)=(x_3     x_5)(x_3     x_4)
\end{align*}
$$

すると、このリストを左右逆にすれば、共通の文字のある２つの互換の積を、先にやった（公式１）

を用いて３次巡回置換に変換した、とみることができます。

$$
\begin{align*}
&(x_1     〇     〇)  型\\
&①       (x_1     x_2)(x_1     x_3)=(x_1     x_2     x_3)\\
&②       (x_1     x_2)(x_1     x_4)=(x_1     x_2     x_4)\\
&③       (x_1     x_2)(x_1     x_5)=(x_1     x_2     x_5)\\
&④       (x_1     x_3)(x_1     x_2)=(x_1     x_3     x_2)\\
&⑤       (x_1     x_3)(x_1     x_4)=(x_1     x_3     x_4)\\
&⑥       (x_1     x_3)(x_1     x_5)=(x_1     x_3     x_5)\\
&⑦       (x_1     x_4)(x_1     x_2)=(x_1     x_4     x_2)\\
&⑧       (x_1     x_4)(x_1     x_3)=(x_1     x_4     x_3)\\
&⑨       (x_1     x_4)(x_1     x_5)=(x_1     x_4     x_5)\\
&⑩       (x_1     x_5)(x_1     x_2)=(x_1     x_5     x_2)\\
&⑪       (x_1     x_5)(x_1     x_3)=(x_1     x_5     x_3)\\
&⑫       (x_1     x_5)(x_1     x_4)=(x_1     x_5     x_4)\\[5pt]
&(x_2     〇     〇)  型\\
&⑬       (x_2     x_3)(x_2     x_4)=(x_2     x_3     x_4)\\
&⑭       (x_2     x_3)(x_2     x_5)=(x_2     x_3     x_5)\\
&⑮       (x_2     x_4)(x_2     x_3)=(x_2     x_4     x_3)\\
&⑯       (x_2     x_4)(x_2     x_5)=(x_2     x_4     x_5)\\
&⑰       (x_2     x_5)(x_2     x_3)=(x_2     x_5     x_3)\\
&⑱       (x_2     x_5)(x_2     x_4)=(x_2     x_5     x_4)\\[5pt]
&(x_3     〇     〇)  型\\
&⑲       (x_3     x_4)(x_3     x_5)=(x_3     x_4     x_5)\\
&⑳       (x_3     x_5)(x_3     x_4)=(x_3     x_5     x_4)
\end{align*}
$$

これで (case3) のすべての互換の積を、３次巡回置換で表すことができました。

(case4)　動かない文字が１つの場合

(case4-1)
　この場合は共通の文字のない２つの互換の積で、次のように①から⑮の $${15}$$ 通りの置換がありました。

（再掲）

$$
\begin{align*}
&(x_1     x_2)(〇     △)  型\\
&①       (x_1     x_2)(x_3     x_4)\\
&②       (x_1     x_2)(x_3     x_5)\\
&③       (x_1     x_2)(x_4     x_5)\\[5pt]
&(x_1     x_3)(〇     △)  型\\
&④       (x_1     x_3)(x_2     x_4)\\
&⑤       (x_1     x_3)(x_2     x_5)\\
&⑥       (x_1     x_3)(x_4     x_5)\\[5pt]
&(x_1     x_4)(〇     △)  型\\
&⑦       (x_1     x_4)(x_2     x_3)\\
&⑧       (x_1     x_4)(x_2     x_5)\\
&⑨       (x_1     x_4)(x_3     x_5)\\[5pt]
&(x_1     x_5)(〇     △)  型\\
&⑩       (x_1     x_5)(x_2     x_3)\\
&⑪       (x_1     x_5)(x_2     x_4)\\
&⑫       (x_1     x_5)(x_3     x_4)\\[5pt]
&(x_2     x_3)(〇     △)  型\\
&⑬       (x_2     x_3)(x_4     x_5)\\[5pt]
&(x_2     x_4)(〇     △)  型\\
&⑭       (x_2     x_4)(x_3     x_5)\\[5pt]
&(x_2     x_5)(〇     △)  型\\
&⑮       (x_2     x_5)(x_3     x_4)
\end{align*}
$$

なお、これらは共通の文字の無い互いに独立な互換の積なので、順番を入れ替えても同じものとなります。
（例）①について
　$${(x_1     x_2)(x_3     x_4)=(x_3     x_4)(x_1     x_2)}$$

これらは、先にやった（公式２）

を用いれば、すべて３次巡回置換で表すことができます。すでにやりましたが、①に関して具体的にやってみると

$$
\begin{align*}
(x_1     x_2)(x_3     x_4)&=(x_1     x_2)\underset{恒等置換を間に挟む}{\underline{(x_2     x_3)(x_2     x_3)}}(x_3     x_4)\\
&=\underset{前の２つをセット}{\underline{(x_1     x_2)(x_2     x_3)}}\,\underset{後ろの２つをセット}{\underline{\underline{(x_2     x_3)(x_3     x_4)}}}\\
&=\underset{先頭の文字をそろえる}{\underline{(x_2     x_1)(x_2     x_3)}}\,\underset{先頭の文字をそろえる}{\underline{\underline{(x_3     x_2)(x_3     x_4)}}}\\
&=\underset{公式１利用}{\underline{(x_2     x_1     x_3)}}\,\underset{公式１利用}{\underline{\underline{(x_3     x_2     x_4)}}}\\
&=\underset{並び替え}{\underline{(x_1     x_3     x_2)}}\,\underset{並び替え}{\underline{\underline{(x_2     x_4     x_3)}}}
\end{align*}
$$

と恒等置換をはさみ込む方法です。この変換を $${15}$$ 通りのすべての置換に実行すると、次のようになります。結果は先頭の文字の添え字の数が、最も小さくなるように整理しています。

$$
\begin{alignat*}{2}
&(x_1     x_2)(〇     △)  型\\
&①       (x_1     x_2)(x_3     x_4) & &=(x_1     x_3     x_2)(x_2     x_4     x_3)\\
&②       (x_1     x_2)(x_3     x_5) & &=(x_1     x_3     x_2)(x_2     x_5     x_3)\\
&③       (x_1     x_2)(x_4     x_5) & &=(x_1     x_4     x_2)(x_2     x_5     x_4)\\[5pt]
&(x_1     x_3)(〇     △)  型\\
&④       (x_1     x_3)(x_2     x_4) & &=(x_1     x_2     x_3)(x_3     x_4     x_2)\\
&⑤       (x_1     x_3)(x_2     x_5) & &=(x_1     x_2     x_3)(x_3     x_5     x_2)\\
&⑥       (x_1     x_3)(x_4     x_5) & &=(x_1     x_4     x_3)(x_3     x_5     x_4)\\[5pt]
&(x_1     x_4)(〇     △)  型\\
&⑦       (x_1     x_4)(x_2     x_3) & &=(x_1     x_2     x_4)(x_4     x_3     x_2)\\
& & &=(x_1     x_2     x_4)(x_2     x_4     x_3)\\
&⑧       (x_1     x_4)(x_2     x_5) & &=(x_1     x_2     x_4)(x_4     x_5     x_2)\\
& & &=(x_1     x_2     x_4)(x_2     x_4     x_5)\\
&⑨       (x_1     x_4)(x_3     x_5) & &=(x_1     x_3     x_4)(x_4     x_5     x_3)\\
& & &=(x_1     x_3     x_4)(x_3     x_4     x_5)\\[5pt]
&(x_1     x_5)(〇     △)  型\\
&⑩       (x_1     x_5)(x_2     x_3) & &=(x_1     x_2     x_5)(x_5     x_3     x_2)\\
& & &=(x_1     x_2     x_5)(x_2     x_5     x_3)\\
&⑪       (x_1     x_5)(x_2     x_4) & &=(x_1     x_2     x_5)(x_5     x_4     x_2)\\
& & &=(x_1     x_2     x_5)(x_2     x_5     x_4)\\
&⑫       (x_1     x_5)(x_3     x_4) & &=(x_1     x_3     x_5)(x_5     x_4     x_3)\\
& & &=(x_1     x_3     x_5)(x_3     x_5     x_4)\\[5pt]
&(x_2     x_3)(〇     △)  型\\
&⑬       (x_2     x_3)(x_4     x_5) & &=(x_2     x_4     x_3)(x_3     x_5     x_4)\\[5pt]
&(x_2     x_4)(〇     △)  型\\
&⑭       (x_2     x_4)(x_3     x_5) & &=(x_2     x_3     x_4)(x_4     x_5     x_3)\\
& & &=(x_2     x_3     x_5)(x_3     x_4     x_5)\\[5pt]
&(x_2     x_5)(〇     △)  型\\
&⑮       (x_2     x_5)(x_3     x_4) & &=(x_2     x_3     x_5)(x_5     x_4     x_3)\\
& & &=(x_2     x_3     x_5)(x_3     x_5     x_4)
\end{alignat*}
$$

これで (case4-1) のすべての互換の積を、３次巡回置換の積で表すことができました。

(case5)　動かない文字が０の場合

(case5-2)
　この場合は５次巡回置換で、次のように①から㉔の $${24}$$ 通りの置換がありました。

（再掲）

$$
\begin{align*}
&(x_1     x_2     〇     △     \square)  型\\
&①       (x_1     x_2     x_3     x_4     x_5)=(x_1     x_2)(x_1     x_3)(x_1     x_4)(x_1     x_5)\\
&②       (x_1     x_2     x_3     x_5     x_4)=(x_1     x_2)(x_1     x_3)(x_1     x_5)(x_1     x_4)\\
&③       (x_1     x_2     x_4     x_3     x_5)=(x_1     x_2)(x_1     x_4)(x_1     x_3)(x_1     x_5)\\
&④       (x_1     x_2     x_4     x_5     x_3)=(x_1     x_2)(x_1     x_4)(x_1     x_5)(x_1     x_3)\\
&⑤       (x_1     x_2     x_5     x_3     x_4)=(x_1     x_2)(x_1     x_5)(x_1     x_3)(x_1     x_4)\\
&⑥       (x_1     x_2     x_5     x_4     x_3)=(x_1     x_2)(x_1     x_5)(x_1     x_4)(x_1     x_3)\\[5pt]
&(x_1     x_3     〇     △     \square)  型\\
&⑦       (x_1     x_3     x_2     x_4     x_5)=(x_1     x_3)(x_1     x_2)(x_1     x_4)(x_1     x_5)\\
&⑧       (x_1     x_3     x_2     x_5     x_4)=(x_1     x_3)(x_1     x_2)(x_1     x_5)(x_1     x_4)\\
&⑨       (x_1     x_3     x_4     x_2     x_5)=(x_1     x_3)(x_1     x_4)(x_1     x_2)(x_1     x_5)\\
&⑩       (x_1     x_3     x_4     x_5     x_2)=(x_1     x_3)(x_1     x_4)(x_1     x_5)(x_1     x_2)\\
&⑪       (x_1     x_3     x_5     x_2     x_4)=(x_1     x_3)(x_1     x_5)(x_1     x_2)(x_1     x_4)\\
&⑫       (x_1     x_3     x_5     x_4     x_2)=(x_1     x_3)(x_1     x_5)(x_1     x_4)(x_1     x_2)\\[5pt]
&(x_1     x_4     〇     △     \square)  型\\
&⑬       (x_1     x_4     x_2     x_3     x_5)=(x_1     x_4)(x_1     x_2)(x_1     x_3)(x_1     x_5)\\
&⑭       (x_1     x_4     x_2     x_5     x_3)=(x_1     x_4)(x_1     x_2)(x_1     x_5)(x_1     x_3)\\
&⑮       (x_1     x_4     x_3     x_2     x_5)=(x_1     x_4)(x_1     x_3)(x_1     x_2)(x_1     x_5)\\
&⑯       (x_1     x_4     x_3     x_5     x_2)=(x_1     x_4)(x_1     x_3)(x_1     x_5)(x_1     x_2)\\
&⑰       (x_1     x_4     x_5     x_2     x_3)=(x_1     x_4)(x_1     x_5)(x_1     x_2)(x_1     x_3)\\
&⑱       (x_1     x_4     x_5     x_3     x_2)=(x_1     x_4)(x_1     x_5)(x_1     x_3)(x_1     x_2)\\[5pt]
&(x_1     x_5     〇     △     \square)  型\\
&⑲       (x_1     x_5     x_2     x_3     x_4)=(x_1     x_5)(x_1     x_2)(x_1     x_3)(x_1     x_4)\\
&⑳       (x_1     x_5     x_2     x_4     x_3)=(x_1     x_5)(x_1     x_2)(x_1     x_4)(x_1     x_3)\\
&㉑       (x_1     x_5     x_3     x_2     x_4)=(x_1     x_5)(x_1     x_3)(x_1     x_2)(x_1     x_4)\\
&㉒       (x_1     x_5     x_3     x_4     x_2)=(x_1     x_5)(x_1     x_3)(x_1     x_4)(x_1     x_2)\\
&㉓       (x_1     x_5     x_4     x_2     x_3)=(x_1     x_5)(x_1     x_4)(x_1     x_2)(x_1     x_3)\\
&㉔       (x_1     x_5     x_4     x_3     x_2)=(x_1     x_5)(x_1     x_4)(x_1     x_3)(x_1     x_2)
\end{align*}
$$

これらは前２つと後ろ２つに分けで、それぞれは共通の文字のある互換の積なので、（公式１）

を用いて３次巡回置換に変換します。例えば①について具体的にやってみると

$$
\begin{align*}
 (x_1     x_2     x_3     x_4     x_5)&=\,\underset{前の２つをセット}{\underline{(x_1     x_2)(x_1     x_3)}}\,\underset{後ろの２つをセット}{\underline{\underline{(x_1     x_4)(x_1     x_5)}}}\\
&=\,\underset{公式１を利用}{\underline{(x_1     x_2     x_3)}}\,\underset{公式１を利用}{\underline{\underline{(x_1     x_4     x_5)}}}
\end{align*}
$$

この変形をすべての置換に実行していくと、次のようになります。

$$
\begin{alignat*}{2}
&(x_1     x_2     〇     △     \square)  型\\
&①       (x_1     x_2     x_3     x_4     x_5) & &=(x_1     x_2)(x_1     x_3)(x_1     x_4)(x_1     x_5)\\
& & &=(x_1     x_2     x_3)(x_1     x_4     x_5)\\
&②       (x_1     x_2     x_3     x_5     x_4) & &=(x_1     x_2)(x_1     x_3)(x_1     x_5)(x_1     x_4)\\
& & &=(x_1     x_2     x_3)(x_1     x_5     x_4)\\
&③       (x_1     x_2     x_4     x_3     x_5) & &=(x_1     x_2)(x_1     x_4)(x_1     x_3)(x_1     x_5)\\
& & &=(x_1     x_2     x_4)(x_1     x_3     x_5)\\
&④       (x_1     x_2     x_4     x_5     x_3) & &=(x_1     x_2)(x_1     x_4)(x_1     x_5)(x_1     x_3)\\
& & &=(x_1     x_2     x_4)(x_1     x_5     x_3)\\
&⑤       (x_1     x_2     x_5     x_3     x_4) & &=(x_1     x_2)(x_1     x_5)(x_1     x_3)(x_1     x_4)\\
& & &=(x_1     x_2     x_5)(x_1     x_3     x_4)\\
&⑥       (x_1     x_2     x_5     x_4     x_3) & &=(x_1     x_2)(x_1     x_5)(x_1     x_4)(x_1     x_3)\\
& & &=(x_1     x_2     x_5)(x_1     x_4     x_3)\\[5pt]
&(x_1     x_3     〇     △     \square)  型\\
&⑦       (x_1     x_3     x_2     x_4     x_5) & &=(x_1     x_3)(x_1     x_2)(x_1     x_4)(x_1     x_5)\\
& & &=(x_1     x_3     x_2)(x_1     x_4     x_5)\\
&⑧       (x_1     x_3     x_2     x_5     x_4) & &=(x_1     x_3)(x_1     x_2)(x_1     x_5)(x_1     x_4)\\
& & &=(x_1     x_3     x_2)(x_1     x_5     x_4)\\
&⑨       (x_1     x_3     x_4     x_2     x_5) & &=(x_1     x_3)(x_1     x_4)(x_1     x_2)(x_1     x_5)\\
& & &=(x_1     x_3     x_4)(x_1     x_2     x_5)\\
&⑩       (x_1     x_3     x_4     x_5     x_2) & &=(x_1     x_3)(x_1     x_4)(x_1     x_5)(x_1     x_2)\\
& & &=(x_1     x_3     x_4)(x_1     x_5     x_2)\\
&⑪       (x_1     x_3     x_5     x_2     x_4) & &=(x_1     x_3)(x_1     x_5)(x_1     x_2)(x_1     x_4)\\
& & &=(x_1     x_3     x_5)(x_1     x_2     x_4)\\
&⑫       (x_1     x_3     x_5     x_4     x_2) & &=(x_1     x_3)(x_1     x_5)(x_1     x_4)(x_1     x_2)\\
& & &=(x_1     x_3     x_5)(x_1     x_4     x_2)\\[5pt]
&(x_1     x_4     〇     △     \square)  型\\
&⑬       (x_1     x_4     x_2     x_3     x_5) & &=(x_1     x_4)(x_1     x_2)(x_1     x_3)(x_1     x_5)\\
& & &=(x_1     x_4     x_2)(x_1     x_3     x_5)\\
&⑭       (x_1     x_4     x_2     x_5     x_3) & &=(x_1     x_4)(x_1     x_2)(x_1     x_5)(x_1     x_3)\\
& & &=(x_1     x_4     x_2)(x_1     x_5     x_3)\\
&⑮       (x_1     x_4     x_3     x_2     x_5) & &=(x_1     x_4)(x_1     x_3)(x_1     x_2)(x_1     x_5)\\
& & &=(x_1     x_4     x_3)(x_1     x_2     x_5)\\
&⑯       (x_1     x_4     x_3     x_5     x_2) & &=(x_1     x_4)(x_1     x_3)(x_1     x_5)(x_1     x_2)\\
& & &=(x_1     x_4     x_3)(x_1     x_5     x_2)\\
&⑰       (x_1     x_4     x_5     x_2     x_3) & &=(x_1     x_4)(x_1     x_5)(x_1     x_2)(x_1     x_3)\\
& & &=(x_1     x_4     x_5)(x_1     x_2     x_3)\\
&⑱       (x_1     x_4     x_5     x_3     x_2) & &=(x_1     x_4)(x_1     x_5)(x_1     x_3)(x_1     x_2)\\
& & &=(x_1     x_4     x_5)(x_1     x_3     x_2)\\[5pt]
&(x_1     x_5     〇     △     \square)  型\\
&⑲       (x_1     x_5     x_2     x_3     x_4) & &=(x_1     x_5)(x_1     x_2)(x_1     x_3)(x_1     x_4)\\
& & &=(x_1     x_5     x_2)(x_1     x_3     x_4)\\
&⑳       (x_1     x_5     x_2     x_4     x_3) & &=(x_1     x_5)(x_1     x_2)(x_1     x_4)(x_1     x_3)\\
& & &=(x_1     x_5     x_2)(x_1     x_4     x_3)\\
&㉑       (x_1     x_5     x_3     x_2     x_4) & &=(x_1     x_5)(x_1     x_3)(x_1     x_2)(x_1     x_4)\\
& & &=(x_1     x_5     x_3)(x_1     x_2     x_4)\\
&㉒       (x_1     x_5     x_3     x_4     x_2) & &=(x_1     x_5)(x_1     x_3)(x_1     x_4)(x_1     x_2)\\
& & &=(x_1     x_5     x_3)(x_1     x_4     x_2)\\
&㉓       (x_1     x_5     x_4     x_2     x_3) & &=(x_1     x_5)(x_1     x_4)(x_1     x_2)(x_1     x_3)\\
& & &=(x_1     x_5     x_4)(x_1     x_2     x_3)\\
&㉔       (x_1     x_5     x_4     x_3     x_2) & &=(x_1     x_5)(x_1     x_4)(x_1     x_3)(x_1     x_2)\\
& & &=(x_1     x_5     x_4)(x_1     x_3     x_2)\\
\end{alignat*}
$$

　これで (case5) のすべての５次巡回置換を、３次巡回置換の積で表すことができました。以上で６０通りすべての遇置換を３次巡回置換、または３次巡回置換の積で表せたことになります」
「なるほど、よくできました。では５次置換のうち、遇置換を３次巡回置換で表せたことにどういう意味があるのか、それが問題だね」
「はい、それが問題です。まだ分かっていないので、５次以上の方程式には解の公式が存在しないことについて、これまでのステップを復習してみます。もう一度最初から眺めることによって、その謎を紐解くヒントが得られそうです」

6. ５次方程式について、これまでのステップを復習

「条件１」を満たす『差積』を添加して、対称性を遇置換シンメトリーまで破壊する

　「まず初めに、「条件Ⅰ」

「条件Ⅰ」
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は５次置換で対称性が壊れているが、$${X^2}$$ では５次置換で対称性を保つ。』

を満たす「解の式」$${X}$$ を考えます。「解の式」$${X}$$ とは、文字通り５次方程式の解
　$${x_1,  x_2,  x_3,  x_4,  x_5}$$
で作られる式のことで、例えば、以下のような式です。
　$${x_1+x_2+x_3+x_4+x_5}$$
　$${x_1x_2x_3x_4x_5}$$
　$${(x_1)^2+(x_2)^2+(x_3)^2+(x_4)^2+(x_5)^2}$$
　$${x_3-2x_5}$$
　$${x_1+4x_2x_3-3x_5+5}$$
　$${\dfrac{x_1-3x_3}{7x_4x_5}}$$
　$${x_1}$$
　$${x_2}$$
$${x_3-2x_5}$$ のようにすべての文字を使う必要はありません。また、$${x_1,  x_2,  \cdots}$$ のように解そのものを表す１文字の式も解の式となります。

　さて、最高次数の係数を $${1}$$ にした５次方程式
　$${x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5}$$
の係数 $${a_1,  a_2,  a_3,  a_4,  a_5}$$ は、基本対称式（及びその $${-1}$$ 倍）になることはすでに勉強しました。よって
　『対称式は基本対称式の加減乗除で表すことができる』
という＜対称式の基本定理＞により、対称式は元の５次方程式の係数で表すことができます。

$$
\begin{align*}
対称式 &\longleftrightarrow 基本対称式で表せる（対称式の基本定理）\\
&\longleftrightarrow ５次方程式の係数で表せる（係数は基本対称式）
\end{align*}
$$

しかし対称式でないものは係数で表すことができません。よって、$${x_1}$$ という解そのものを表す式も、対称式ではないので係数の加減乗除で表すことはできません。これは、係数の加減乗除だけでは解の公式を表せないことを意味しています。
　そこで、なんらかの”新しい数”を追加（添加）し、使える式の集まり（集合）を拡大する必要があります。この”新しい式”は、それまでに使えた”古い式”の累乗根です。具体的には、対称性（シンメトリー）をもつ「解の式」の累乗根です。この累乗根という”新しい数”の添加によって、使える式の範囲を拡大すると同時に、使える式の対称性を破壊していきます。そして、最終的に完全に対称性の失われた「恒等置換でした対称性を保てないレベル」にまで対称性が破壊できれば、その段階で使える”新しい数”を用いて解の公式を構成することが可能となります。
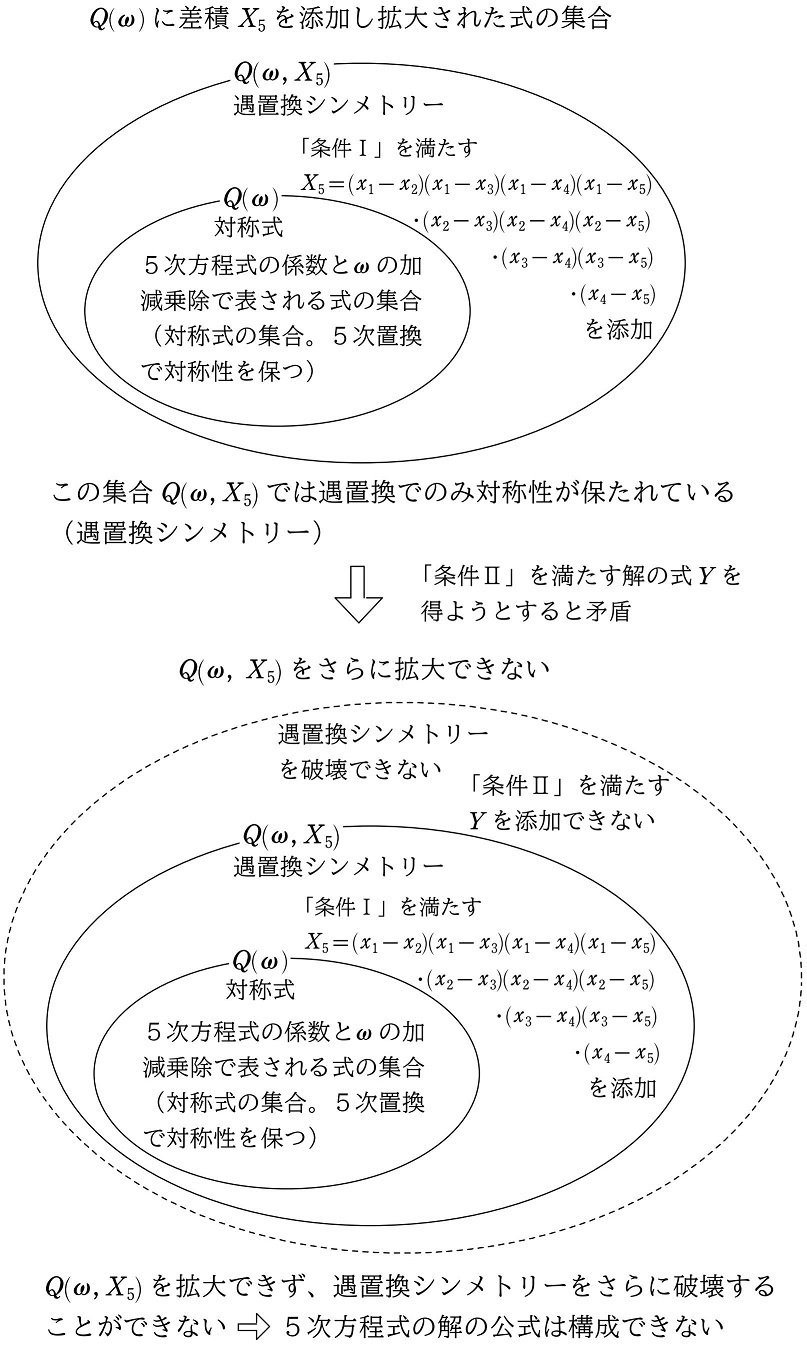
　そこでまず５次方程式では、第１段階として「条件Ⅰ」を満たす「解の式」$${X}$$ として、差積 $${X_5}$$ を $${Q(\omega)}$$ に添加して、 $${Q(\omega,  X_5)}$$ という集合を考えました。 $${Q(\omega)}$$ とは５次方程式の係数の加減乗除で表される式の集合 $${Q}$$ に $${\omega}$$ を添加した集合です（$${\Rightarrow}$$ 詳しくは本シリーズ (14)）。なお $${\omega}$$ は３乗して１になる数（１の３乗根）のうち、複素数であるものです。
　改めてまとめますと、$${x^5}$$ の係数を $${1}$$ とした５次方程式
　$${x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0}$$
において
　$${Q}$$ は、係数 $${a_1,  a_2,  a_3,  a_4,  a_5}$$ の加減乗除で表せる式全体の集合
　$${Q(\omega)}$$ は、係数 $${a_1,  a_2,  a_3,  a_4,  a_5}$$ と $${\omega}$$ の加減乗除で表せる式全体の集合
　$${Q(\omega,  X_5)}$$ は、係数 $${a_1,  a_2,  a_3,  a_4,  a_5}$$ と $${\omega}$$ と差積 $${X_5}$$ の加減乗除で表せる式全体の集合となります（本シリーズ (14)）。
　このように、次々と使える数や式（使える道具）を添加していくことによって、解の公式を導くために必要な式を拡大していきます。その添加された $${X_5}$$ は上記の「条件Ⅰ」を満たす $${X}$$ のことで、５次方程式の５つの解 $${x_1,  x_2,  x_3,  x_4,  x_5}$$ を用いて次のような差積で表現できます。

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

この解の差積 $${X_5}$$ を $${Q(\omega)}$$ に添加することによって、対称性を保つ置換を５次置換から遇置換まで絞り込むことに成功、いわば、完全なる対称性（対称式）を遇置換シンメトリーまで破壊すことができたわけです（$${\Rightarrow}$$ 詳しくは本シリーズ (14)）。

$$
\begin{gather*}
Q(\omega)\\
\hspace{67pt}\downarrow  \Leftarrow  X_5 の添加\\
Q(\omega,  X_5)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf ５次置換（対称式）}\\
\hspace{67pt}\downarrow  \Leftarrow  X_5 の添加\\
{\bf 遇置換シンメトリー}
\end{gather*}
$$

　添加による使える式の拡大と対称性を保つ置換には、上記のような”対応関係”があること、つまり
　『使える式が拡大するにつれて、対称性を保つ置換は逆に絞られていく』
ことが重要です。使える式が大きくなると、それに反して置換は少なくなるわけです。最終的に、対称性を保つ置換が恒等置換１つだけになるまで使える式を添加していきます。恒等置換でしか対称性を保てない式は、完全に対称性が壊れています。つまり対称性を保つ置換が恒等置換だけになれば、その集合内では完全に対称性の壊れた「解の公式」を作り上げることができるわけです（注２）。
　さて、２次以上の方程式は、何次であってもその解を用いて差積を作ることができます。具体的には、２次方程式では、その２つの解を $${\alpha,  \beta}$$ とすると

$$
\begin{align*}
X_2=\alpha-\beta
\end{align*}
$$

３次方程式では、その３つの解を $${\alpha,  \beta,  \gamma}$$ とすると

$$
\begin{align*}
X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$

４次方程式では、その４つの解を $${x_1,  x_2,  x_3,  x_4}$$ とすると

$$
\begin{align*}
X_4=(x_1-x_2)(x_1-x_3)(x_1-x_4)&\\
\cdot\,(x_2-x_3)(x_2-x_4)&\\
\cdot\,(x_3-x_4)&
\end{align*}
$$

と、その解を用いて差積を作ることができます。そしてこの差積の添加によって、完全なシンメトリー（対称式）を遇置換シンメトリーにまで破壊することが可能となります。差積の添加は、対称性を遇置換シンメトリーまで破壊する常套手段です。５次方程式においても、差積 $${X_5}$$ の添加によって、完全なシンメトリーを遇置換シンメトリーまで破壊することができました。
　さて次は、この遇置換シンメトリーをどのように破壊していくか、ということです。そこで次の「条件Ⅱ」を考えます。

「条件Ⅱ」を用いて、さらに遇置換シンメトリーを破壊する

　遇置換シンメトリーをさらに破壊するために、５次方程式においても、次の「条件Ⅱ」を満たす解の式 $${Y}$$ を考えます（注３）。

「条件Ⅱ」
　『$${Y}$$ はある遇置換で変化するが、$${Y^3}$$ はすべての遇置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は遇置換で対称性が壊れているが、$${Y^3}$$ は遇置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

　なお「$${Y^3}$$ は対称式ではない」という補足は、「条件Ⅰ」を満たす式 $${X_5}$$ の添加によって、対称性はすでに遇置換シンメトリーまで破壊されているからです。遇置換シンメトリーを保つ式体系の中で、新たに「条件Ⅱ」を満たす式を添加することでさらに対称性を破壊していきます。
　３次方程式の場合、この「条件Ⅱ」を満たす式 $${Y}$$ はラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
でした。この $${A}$$ は遇置換で変化しますが、その３乗
　$${A^3=(\alpha+\omega\beta+\omega^2\gamma)^3}$$
は遇置換で変化しません（注４）（$${\Rightarrow}$$ 詳しくは本シリーズ(13)）。
　なお $${A^3}$$ は、例えば互換 $${(\alpha     \beta)}$$ で違う式に変化するので対称式ではありません。つまり $${A^3}$$ は「条件Ⅱ」の補足である「対称式ではない」という条件も満たしています（注５）。
　このラグランジュ・リゾルベント $${A}$$ を$${Q(\omega,  X_3)}$$ に添加することによって、対称性を保つ置換を遇置換から恒等置換にまで絞り込むことができ、３次方程式の解の公式が実現できました（$${\Rightarrow}$$ 詳しくは本シリーズ (12)、(13) ）。

$$
\begin{gather*}
Q(\omega)\\
\hspace{66pt}\downarrow  \Leftarrow  X_3 の添加\\
Q(\omega,  X_3)\\
\hspace{63pt}\downarrow  \Leftarrow  A の添加\\
Q(\omega,  X_3,  A)
\end{gather*}
\hspace{15pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf ３次置換（対称式）}\\
\hspace{66pt}\downarrow  \Leftarrow  X_3 の添加\\
{\bf 遇置換シンメトリー}\\
\hspace{63pt}\downarrow  \Leftarrow  A の添加\\
{\bf 恒等置換}
\end{gather*}
$$

　解の公式が構成できる都合のいい式の添加により、利用できる式の世界（集合）を広げていきます。その添加した式の対称性に依存して、使える式の世界の対称性は絞られて（破壊されて）いきます。いわば、使える式が大きくなるにつれて、対称性は逆に小さくなっていくわけです。
　解の公式が存在するということは、置換の言葉で言えば「対称性が恒等置換まで破壊される」ということです。
　ではなぜ恒等置換まで破壊させる必要があるのか。その理由は、解の式 $${x_1,  x_2,  \cdots}$$ のすべてを変化せない置換は恒等置換のみだからです。例えば、３次方程式の解 $${x_1,  x_2,  x_3}$$ に恒等置換を作用させても、$${x_1,  x_2,  x_3}$$ はいずれも変化しません。

$$
\begin{align*}
x_1       &x_2       x_3\\
&\downarrow　{\small 恒等置換を作用}\\
x_1       &x_2       x_3　{\small \Leftarrow いずれも変化しない}
\end{align*}
$$

解の公式は文字通り解を表す式なので、解の式 $${x_1,  x_2,  \cdots}$$ と同等の対称性をもちます。よって、次々と都合のいい式（使える式）を添加していき、構成可能な式の対称性を最終的に恒等置換にまで破壊できれば、それまでに添加されたすべての式の加減乗除によって、いよいよ解の公式が実現できるわけです。
　以上のことを集合として簡単に図式化（イメージ化）すると、以下のようになります。

　差積 $${X_3}$$ を添加することと、差積の２乗の平方根 $${\sqrt{(X_3)^2}}$$ を添加することは同じなので、$${X_3}$$ の添加によって平方根 $${\sqrt{(X_3)^2}}$$ の利用が可能となります（本シリーズ (14)）。
　また、ラグランジュ・リゾルベント $${A}$$ を添加することと、その３乗の３乗根 $${\sqrt[3]{A^3}}$$ を添加することは同じなので、$${A}$$ の添加によって３乗根 $${\sqrt[3]{A^3}}$$ の利用が可能となります（本シリーズ (14)）。
　それら累乗根（平方根、３乗根）を計算に用いることによって、（対称性が恒等置換にまで破壊されている）３次方程式の解の公式が実現できました（$${\Rightarrow}$$ 詳しくは本シリーズ (12)、(13) ）。

　では５次方程式の場合はどうでしょうか。「条件Ⅰ」を満たす差積 $${X_5}$$ の添加によって遇置換シンメトリーまで対称性を破壊することができました。さらに次のステップとして、「条件Ⅱ」を満たす解の式 $${Y}$$ を具体的に構成できれば、３次方程式と同様に、遇置換シンメトリーをさらに破壊することが期待できます。

　そこで、５次方程式において「条件Ⅱ」を満たす解の式 $${Y}$$ を考えます。ここで最初に述べた
　『すべての遇置換は３次巡回置換で表すことができる』
という性質を使います。遇置換はすべて３次巡回置換で表せることから、「条件Ⅱ」

「条件Ⅱ」
　『$${Y}$$ はある遇置換で変化するが、$${Y^3}$$ はすべての遇置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は遇置換で対称性が壊れているが、$${Y^3}$$ は遇置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

について、「遇置換」を「３次巡回置換」に言い換えることができます。

「条件Ⅱ」（３次巡回置換バージョン）
　『$${Y}$$ はある３次巡回置換で変化するが、$${Y^3}$$ はすべての３次巡回置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は３次巡回置換で対称性が壊れているが、$${Y^3}$$ は３次巡回置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

遇置換の代わりに３次巡回置換を使って議論しても同じこととなります。
　すると、前半の条件『$${Y}$$ は３次巡回置換で変化する』ことから、 $${Y}$$ を変化させる３次巡回置換が少なくとも１つ存在することになります。『$${Y}$$ は”ある”３次巡回置換で変化する』と「ある」という言葉を使っているのはそういう意味です（注６）。
　そのある３次巡回置換を $${(i     j     k)}$$ とおきます。すると、$${Y}$$ にその $${(i     j     k)}$$ を作用させると別の式 $${Y'}$$ に変化するので
　$${(i     j     k)Y=Y'\,(\ne Y)　\cdots ①}$$
なお $${(i     j     k)Y}$$ とは、式 $${Y}$$ に３次巡回置換 $${(i     j     k)}$$ を作用させるという意味です（注７）。式 $${Y}$$ の文字に対して
　$${i \rightarrow j \rightarrow k \rightarrow i}$$
と文字を置換せよ、という命令です。
　また、後半の条件『$${Y^3}$$ は３次巡回置換で変化しない』ことから、$${Y^3}$$ に３次巡回置換 $${(i     j     k)}$$ を作用させても変化しないので
　$${(i     j     k)Y^3=Y^3　\cdots ②}$$
ここで、この式の左辺について考えます。 $${(i     j     k)}$$ は $${Y}$$ だけに作用し、指数部分の $${3}$$ 乗は変化させません。つまり、$${Y^3}$$ に $${(i     j     k)}$$ を作用させるということは、$${Y}$$ に $${(i     j     k)}$$ を作用させたものを $${3}$$ 乗するということなので
　$${(i     j     k)Y^3=(i     j     k)Y\cdot(i     j     k)Y\cdot(i     j     k)Y}$$
より
　$${(i     j     k)Y^3=\{{(i     j     k)Y}\}^3　\cdots ③}$$
$${③=②}$$ より
　$${\{(i     j     k)Y\}^3=Y^3}$$
すると $${(i     j     k)Y}$$ は一時的に
　$${(i     j     k)Y=Y,  \omega Y,  \omega^2Y}$$
となりますが（注８）、$${①}$$ より $${(i     j     k)Y\ne Y}$$ なので、$${Y}$$ は却下されて
　$${(i     j     k)Y=\omega Y,  \omega^2Y　\cdots ④}$$
ただし、$${\omega}$$ は「$${3}$$ 乗して $${1}$$ になる数（$${1}$$ の $${3}$$ 乗恨）のうち、$${1}$$ ではない数」です。具体的には虚数
　$${\omega=\dfrac{1+\sqrt{3}i}{2}}$$　または　$${\dfrac{1-\sqrt{3}i}{2}}$$
となります（$${\Rightarrow}$$ 詳しくは本シリーズ (2)）。
　ここで分かったことは、「条件Ⅱ」を満たす解の式 $${Y}$$ は、ある３次巡回置換 $${(i     j     k)}$$ によって
　$${(i     j     k)Y=\omega Y}$$
または
　$${(i     j     k)Y=\omega^2Y}$$
に変化しなければならない、ということです。３次方程式の場合、その解の式 $${Y}$$ はラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
であることはすでにやりました（本シリーズ (13)）。

（補足を追記）

（補足始め）
　３次巡回置換については本シリーズ (14) で初めて登場します。しかし、本シリーズ (13) の段階では３次巡回置換の解説はまだしていないので、３次方定式の解の公式の「条件Ⅱ」については、簡単のために遇置換のままで証明しています。
　具体的には、$${Y}$$（つまりラグランジュ・リゾルベント $${A}$$） に遇置換（ただし恒等置換以外）を作用させると、$${A}$$ は $${\omega}$$ 倍か $${\omega^2}$$ 倍に変化することを証明し、それによって遇置換シンメトリーが破壊されると解説しています（注４）。

　$${(恒等置換以外の遇置換)A=\omega A}$$
または
　$${(恒等置換以外の遇置換)A=\omega^2A}$$

結局、３次置換においては遇置換（$${①、➁、➂}$$）は３次巡回置換そのものなので、問題はありませんでした（本シリーズ (14)）。$${Y}$$ としてラグランジュ・リゾルベント $${A}$$ を取れることには違いはありません。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

　５次方程式においては「遇置換は３次巡回置換で表せる」という定理が本質的に必要になってくるので、３次方程式においても、先に３次巡回置換を解説してから「条件Ⅱ」（３次巡回置換バージョンとして）を提示した方が分かりやすかったかもしれません。その方が５次方程式との関連が見えやすくなりそうです（後で修正するかも）。
　遅ればせながら、ラグランジュ・リゾルベント $${A}$$ に３次巡回置換を作用させると $${\omega}$$ 倍か $${\omega^2}$$ 倍に変化することの証明は、（注４）で行いました。
（補足終わり）

　その $${A}$$ に３次巡回置換 $${(\alpha     \beta     \gamma)}$$ を作用させると
　$${(\alpha     \beta     \gamma)A=\omega^2A}$$
と $${\omega^2}$$ 倍となり、３次巡回置換 $${(\alpha     \gamma     \beta)}$$ を作用させると
　$${(\alpha     \gamma     \beta)A=\omega A}$$
と $${\omega}$$ 倍になり、確かに $${\omega}$$ 倍か、 $${\omega^2}$$ 倍に変化しています（注４で証明）。５次方程式においても、「条件Ⅱ」を満たす解の式 $${Y}$$ に３次巡回置換を作用させると、それは $${Y}$$ の$${\omega}$$ 倍か、 $${\omega^2}$$ 倍になることは先ほど示しました。
　ここまでは３次方程式のときと同じ筋書きで問題無いように思えます。５次方程式においても、３次方程式と同様に「条件Ⅱ」をみたす解の式 $${Y}$$ を添加すれば、遇置換シンメトリーをさらに破壊することが期待できます。しかし・・・」
「しかし？」
「５次方程式の場合、都合のいい解の式 $${Y}$$ が、具体的に作れないように思えます・・・」
「そうそう。３次方程式のときのラグランジュリゾルベントのように、作れるんだったら具体的に作ればいいんだね。ではもし作れないとすると？」
「対称性の破壊は遇置換シンメトリーでストップ、最終的に恒等置換にまで破壊することが不可能となるので、５次方程式に解の公式が存在すると仮定したことに矛盾します」
「そう。矛盾が導き出せたので、背理法により５次方程式に解の公式が存在しないことが証明できる」

「では森田君、どうやって $${Y}$$ が作れないことを証明する？」
「うーん・・・」森田君は悩み込む。
「では森田君」いよいよとばかり竹村が口を開いた。
「同じ３次巡回置換は何回作用させると元に戻る？」
「３回です」
「では５次巡回置換は？」
「５回です、あっ！」
　森田君は口を開いた。
「遇置換は必ず３次巡回置換で表せることは勉強しました。すると・・・」
「すると？」
「すべての３次巡回置換が５次巡回置換で表せるとしたら・・・、そうか！」
　森田君はもの凄いスピードでホワイトボードに図形を書き始めた。竹村はホワイトボードを凝視した。

（続く）

（コメント）
　結論まで書くつもりでしたが、途中で息切れしてきたので、とりあえずここまでとなります。「すべての３次巡回置換は５次巡回置換の積で表せる」ということから矛盾が生じ、解の公式が存在しないことが証明されますが、どうまとめるか考慮中です。
　あと（注）が本文より長く？なってしまいました。本シリーズで既に述べたことも（注）で書いています。必要なのかどうか、むしろ分かりにくくなりそうな気もしますが、もう少し整理した形にできればと思います。
　特に（注２）（注３）はうまく記述できているのか分からないので、何か気付いたら随時修正していきます。

（注１）３次置換のうち、遇置換を３次巡回置換で表す（復習）。

　３次置換のうち、遇置換をすべて３次巡回置換で表す（本シリーズ (14)）。恒等置換は、同じ３次巡回置換を３回連続作用させることによって表すことができる。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換
\end{align*}
$$

①は同じ３次巡回置換 $${(\alpha     \beta     \gamma)}$$ を連続３回作用させるので、結局元に戻って同じになる。つまり作用させても何も変化しないので恒等置換 $${I}$$ と同じ。一般に
『すべての遇置換は３次巡回置換（およびその積）で表すことができる』
この事実は、５次以上の方程式に解の公式が存在しないことの証明で利用される。

（注２）解の公式の対称性について（復習）

　２次方程式 $${ax^2+bx+c=0}$$ の解の公式は

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

と表せます。ここで $${\pm}$$ それぞれについて、プラスの方を
　$${\alpha=\dfrac{-b+\sqrt{b^2-4ac}}{2a}}$$
マイナスの方を
　$${\beta=\dfrac{-b-\sqrt{b^2-4ac}}{2a}}$$
と置きます。この解 $${\alpha,  \beta}$$ の置換には
　①　$${\dbinom{\alpha       \beta}{\alpha       \beta}=I}$$
と
　➁　$${\dbinom{\alpha       \beta}{\beta       \alpha}=(\alpha     \beta)}$$
の２つがあります。①は何も変化しない恒等置換 $${I}$$、②は $${\alpha}$$ と $${\beta}$$ を入れ替えるので互換 $${(\alpha     \beta)}$$ となります。
　さて、２つの解 $${\alpha,  \beta}$$ を、$${\alpha}$$ は $${\alpha}$$ のまま、かつ $${\beta}$$ は $${\beta}$$ のままで変化させない置換は恒等置換 $${I}$$ のみです。

$$
\begin{align*}
&\alpha       \beta\\
&\hspace{6pt}\Downarrow　{\small 恒等置換  I  を作用}\\
&\alpha       \beta　\leftarrow {\small 変化しない}
\end{align*}
$$

つまり、解を表す１文字の式 $${\alpha,  \beta}$$ そのものは、「恒等置換でしか対称性を保つことのできない、完全に対称性の壊れた式」となります。よって、その $${\alpha,  \beta}$$

　$${\alpha=\dfrac{-b+\sqrt{b^2-4ac}}{2a}}$$

　$${\beta=\dfrac{-b-\sqrt{b^2-4ac}}{2a}}$$

を１つの式で表した解の公式

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

も、完全に対称性の壊れた式です。このように解の公式を導くためには「恒等置換でしか対称性を保つことのできない、完全に対称性の壊れた式」を構成することが必要です。そのための手段として、２次方程式では差積 $${X_2}$$
　$${X_2=\alpha-\beta}$$
の添加というアイデアがありました（$${\Rightarrow}$$ 詳しくは本シリーズ (11)、(13)）。このことは３次方程式、４次方程式と次数が高くなっても同じです。５次方程式の解を
　 $${x_1,  x_2,  x_3,  x_4,  x_5}$$
とすると、その解の置換（５次置換）は１２０通りありました。そのうち$${x_1}$$ は $${x_1}$$ のまま、かつ $${x_2}$$ は $${x_2}$$ のまま、かつ $${x_3}$$ は $${x_3}$$ のまま、 かつ $${x_4}$$ は $${x_4}$$ のまま、かつ $${x_5}$$ は $${x_5}$$ のままと、すべての解を変化させない置換は恒等置換 $${I}$$ のみです。

$$
\begin{align*}
x_1       x_2       &x_3       x_4       x_5\\
&\Downarrow　{\small 恒等置換  I  を作用}\\
x_1       x_2       &x_3       x_4       x_5　\leftarrow {\small 変化しない}
\end{align*}
$$

仮に互換 $${(x_1     x_2)}$$ を作用させると、$${x_3,  x_4,  x_5}$$ は変化しませんが、$${x_1}$$ と $${x_2}$$ は入れ替わるので変化します。

$$
\begin{align*}
x_1       x_2       &x_3       x_4       x_5\\
&\Downarrow　{\small 互換  (x_1,  x_2)  を作用}\\
x_2       x_1       &x_3       x_4       x_5　\leftarrow {\small x_1  と  x_2  は変化する}
\end{align*}
$$

つまり、解を表す１文字の式 $${x_1,  x_2,  x_3,  x_4,  x_5}$$ そのものは、「恒等置換でしか対称性を保つことができない、完全に対称性の壊れた式」となります。解の公式とは
　$${x_1=・・・・・・}$$
　$${x_2=・・・・・・}$$
　　$${\vdots}$$
と表せたものを、１つの文字 $${x}$$ を使って
　$${x=・・・・・・}$$
と書いたものです。すなわち解の公式は、$${x_1,  x_2,  x_3,  x_4,  x_5}$$ と同等の対称性をもつ「恒等置換でしか対称性を保つことのできない、完全に対称性の壊れた式」となります。３次置換においては、差積 $${X_3}$$

$$
\begin{align*}
X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$

の添加によって、３次置換の対称性（対称式）を遇置換シンメトリーまで破壊することができました（$${\Rightarrow}$$ 詳しくは本シリーズ (12)）。それと同様に、５次置換に置いても、差積 $${X_5}$$

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

の添加によって、５次置換の対称性（対称式）を遇置換シンメトリーまで破壊することができました（$${\Rightarrow}$$ 詳しくは本シリーズ (14)）。差積の添加は対称性を遇置換シンメトリーまで破壊する常套手段ですが、解の公式を導き出すためには、さらに都合のいい解の式の添加によって、遇置換シンメトリーを破壊し、最終的に対称性を保つ置換を恒等置換にまで絞り込むことが必要です。３次方程式ではそれを担ったのはラグランジュ・リゾルベント $${A}$$
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
の添加でした（$${\Rightarrow}$$ 詳しくは本シリーズ (13)）。しかし５次以上の方程式では解の公式は存在しないので、５次置換においては対称性を保つ置換を恒等置換にまで絞り込むことはできないことになります。それを証明することが本シリーズでのメインテーマです。

（注３）「条件Ⅱ」を厳密化

　本文で述べた「条件Ⅱ」

「条件Ⅱ」
　『$${Y}$$ はある遇置換で変化するが、$${Y^3}$$ はすべての遇置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は遇置換で対称性が壊れているが、$${Y^3}$$ は遇置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

について、厳密には $${3}$$ 乗のところを $${p}$$ 乗にして議論しなければなりません。次がその $${p}$$ 乗のバージョンです。

「条件Ⅱ」（$${p}$$ 乗のバージョン）
　『$${Y}$$ はある遇置換で変化するが、$${Y^p}$$ はすべての遇置換で変化しない（ただし $${Y^p}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は遇置換で対称性が壊れているが、$${Y^p}$$ は遇置換で対称性が保たれている（ただし $${Y^p}$$ 対称式ではない）』

本シリーズでは初めから $${p=3}$$ として議論を進めていますが、実際はその値で決まっているわけではなく、「条件Ⅱ」を満たす $${Y}$$ が存在するためには $${p=3}$$ であることを証明する必要があります。本文ではこの証明を割愛しました（この証明を本文中に入れるかどうか検討中。やや難しく長くなるので（注３）にしました）。
　$${p=3}$$ を証明するための全体の流れは、
『$${Y}$$ は遇置換で変化するが、$${Y^p}$$ は遇置換で変化しない（ただし $${Y^p}$$ は対称式ではない）』
より、ある遇置換で $${Y}$$ が $${Y'\,(\ne Y)}$$ に変化したとすると、その $${Y'}$$ は
　$${Y'=\omega_p Y}$$
ただし $${\omega_p}$$ は $${1}$$ の $${p}$$ 乗恨（$${p}$$ 乗すると $${1}$$ になる数のうち $${1}$$ ではない数）と表すことができ、かつ遇置換は３次巡回置換で表せることから、同じ３次巡回置換は３回作用させると元に戻るという性質により
　$${p=3}$$
と決定するという流れです。なお $${p}$$ は素数となります。その理由は（注３）の最後に述べます。
　さて、本題である $${p=3}$$ となる証明を述べていきます。
　まず
　『すべての遇置換は３次巡回置換で表すことができる』
ことから、「条件Ⅱ」の $${p}$$ 乗のバージョンについて、遇置換を３次巡回置換に書き換えることができます。

$${\boldsymbol{Y}}$$ の「条件Ⅱ」（$${p}$$ 乗のバージョン）
　『$${Y}$$ はある３次巡回置換で変化するが、$${Y^p}$$ はすべての３次巡回置換で変化しない（ただし $${Y^p}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は３次巡回置換で対称性が壊れているが、$${Y^p}$$ は３次巡回置換で対称性が保たれている（ただし $${Y^p}$$ 対称式ではない）』

　この「条件Ⅱ」を満たす $${Y}$$ が存在したとします。すると、前半の条件『$${Y}$$ はある３次巡回置換で変化する』ことから、 $${Y}$$ を変化させる３次巡回置換が少なくとも１つ存在することになります。『$${Y}$$ は”ある”３次巡回置換で変化する』と「ある」という言葉を使っているのはそういう意味です（注６）。
　そのある３次巡回置換を $${(i     j     k)}$$ とおきます。$${Y}$$ にその $${(i     j     k)}$$ を作用させると別の式 $${Y'}$$ に変化するので
　$${(i     j     k)Y=Y'\,(\ne Y)　\cdots ①}$$
なお $${(i     j     k)Y}$$ とは、式 $${Y}$$ に３次巡回置換 $${(i     j     k)}$$ を作用させるという意味です。式 $${Y}$$ の文字にたいして
　$${i \rightarrow j \rightarrow k \rightarrow i}$$
と文字を置換せよ、という命令です。
また、後半の条件『$${Y^p}$$ は３次巡回置換で変化しない』ので、$${Y^p}$$ に３次巡回置換 $${(i     j     k)}$$ を作用させても $${Y^p}$$ は変化しません。つまり
　$${(i     j     k){Y^p}=Y^p　\cdots ②}$$
ここで、この式の左辺について考えてみます。$${(i     j     k)}$$ は $${Y}$$ だけに作用し、指数部分の $${p}$$ 乗は変化させません。つまり、$${Y^p}$$ に $${(i     j     k)}$$ を作用させるということは $${Y}$$ に $${(i     j     k)}$$ を作用させたものを $${p}$$ 回掛けるということなので
　$${(i     j     k)Y^p=\underbrace{(i     j     k)Y\cdot(i     j     k)Y\cdots(i     j     k)Y}_{p  個の積}}$$
より
　$${(i     j     k)Y^p=\{(i     j     k){Y}\}^p　\cdots ③}$$
$${③=②}$$ より
　$${\{(i     j     k){Y}\}^p=Y^p　\cdots ④}$$
$${①}$$ を $${④}$$ に代入して
　$${{(Y’)}^p=Y^p     \cdots ⑤}$$
これを $${Y'}$$ について解くと
　$${Y'=\omega_p Y    \cdots ⑥}$$
ただし $${\omega_p}$$ は「$${p}$$ 乗して $${1}$$ になる数（$${1}$$ の $${p}$$ 乗恨）のうち $${1}$$ ではない数」です。つまり $${\omega_p}$$ は
　$${(\omega_p)^p=1    \cdots ⑦}$$
かつ
　$${\omega_p\ne1    \cdots ⑧}$$
を満たす定数となります。

　ここは抽象的なので、具体的な例をあげて考えてみる。$${p}$$ のままだと抽象的なので、$${p=2}$$ のとき、$${p=3}$$ のときと具体的に考えるとわかりやすい。
＜$${\boldsymbol{p=2}}$$ のとき＞
　$${⑤}$$ 式 $${{(Y’)}^p=Y^p}$$ について $${p=2}$$ とすると
　$${{Y’}^2=Y^2}$$
これを $${Y'}$$ について解くと
　$${Y’=\pm Y}$$
ただし $${①}$$ より $${Y'\ne Y}$$ であったので、プラスの方は却下されて
　$${Y’=-Y     \cdots (*1)}$$
よって $${Y'}$$ は、$${Y}$$ の $${-1}$$ 倍と決定します。
　以上のことを $${⑥}$$ 式
　$${Y'=\omega_p Y    \cdots ⑥}$$
で用いた $${\omega_p}$$ を用いて、同じく $${(*1)}$$ を導いてみる。
　$${⑤}$$ 式 $${{(Y’)}^p=Y^p}$$ について $${p=2}$$ とすると
　$${(Y’)^2=Y^2}$$
これを $${Y'}$$ について解くと、$${⑥}$$ について $${p=2}$$ として
　$${Y'=\omega_2Y　\cdots (*2)}$$
ただし $${\omega_2}$$ は、「$${2}$$ 乗して $${1}$$ になる数（$${1}$$ の平方根 $${1,  -1}$$）のうち $${1}$$ ではない数」なので
　$${\omega_2=-1}$$
これを $${(*2)}$$ に代入して
　$${Y'=-Y}$$
となり、これは $${(*1)}$$ と一致します。

＜$${\boldsymbol{p=3}}$$ のとき＞
　$${⑤}$$ 式 $${{(Y’)}^p=Y^p}$$ について $${p=2}$$ とすると
　$${(Y’)^3=Y^3}$$
これを $${Y'}$$ について解くと
　$${Y’=Y,  \omega Y,  \omega^2Y}$$
ただし $${①}$$ より $${Y'\ne Y}$$ であったので、$${Y}$$ は却下されて
　$${Y’=\omega Y,  \omega^2Y     \cdots (*3)}$$
よって $${Y'}$$ は、$${Y}$$ の $${\omega}$$ 倍か、または $${\omega^2}$$ 倍と決定します。
　なお $${\omega}$$ は、「$${3}$$ 乗して $${1}$$ になる数（$${1}$$ の $${3}$$ 乗恨 $${1,  \omega,  \omega^2}$$）のうち $${1}$$ ではない数」です。具体的には虚数
　$${\omega=\dfrac{1+\sqrt{3}i}{2}}$$　または　$${\dfrac{1-\sqrt{3}i}{2}}$$
となります。
　以上のことを $${⑥}$$ 式
　$${Y'=\omega_p Y    \cdots ⑥}$$
で用いた $${\omega_p}$$ を用いて、同じく $${(*3)}$$ を導いてみる。
　$${⑤}$$ 式 $${{(Y’)}^p=Y^p}$$ について $${p=2}$$ とすると
　$${(Y’)^3=Y^3}$$
これを $${Y'}$$ について解くと、$${⑥}$$ について $${p=3}$$ として
　$${Y'=\omega_3 Y　\cdots (*4)}$$
ただし $${\omega_3}$$ は、「$${3}$$ 乗して $${1}$$ になる数（$${1}$$ の $${3}$$ 乗恨 $${1,  \omega,  \omega^2}$$）のうち $${1}$$ ではない数」なので
　$${\omega_3=\omega,  \omega^2}$$
これを $${(*4)}$$ に代入して
　$${Y’=\omega Y,  \omega^2Y}$$
となり、これは $${(*3)}$$ と一致します。

　さらに、$${①}$$ 式
　$${(i     j     k)Y=Y'\,(\ne Y)　\cdots ①}$$
に $${⑥}$$ 式
　$${Y'=\omega_p Y    \cdots ⑥}$$
を代入して
　$${(i     j     k)Y=\omega_p Y      \cdots ⑨}$$
この式は、$${Y}$$ に３次巡回置換  $${(i     j     k)}$$ を作用させると「$${Y}$$ は $${\omega_p(\ne1)}$$ 倍に変化する」ということを意味しています。$${Y}$$ の変化は $${\omega_p(\ne1)}$$ 倍という限定的な変化です。
　さて、ここから $${p}$$ を求める作業に入ります。３次巡回置換 $${(i     j     k)}$$ は連続３回作用させると元に戻る、つまり３回連続の作用で恒等置換 $${I}$$ となるので
　$${(i     j     k)(i     j     k)(i     j     k)=I}$$
すると、恒等置換 $${I}$$ は $${Y}$$ に作用させても変わらないので
　$${Y=IY}$$
より
　$${Y=(i     j     k)(i     j     k)(i     j     k)Y}$$
右辺について、まずは１つ目の $${(i     j     k)}$$ を $${Y}$$ に作用させると
　$${Y=(i     j     k)(i     j     k)\{(i     j     k)Y\}}$$
中カッコ $${\{\hspace{16pt}\}}$$ から先に計算してきます。この中カッコに $${⑨}$$ 式
　$${(i     j     k)Y=\omega_p Y      \cdots ⑨}$$
を代入すると
　$${Y=(i     j     k)(i     j     k)\{\omega_p Y\}}$$
$${(i     j     k)}$$ が作用するのは $${Y}$$ なので、$${(i     j     k)}$$ を $${Y}$$ の前に書いて
　$${Y=(i     j     k)\omega_p\{(i     j     k)Y\}}$$
再びこの中カッコ $${\{\hspace{16pt}\}}$$ に $${⑨}$$ を代入すると
　$${Y=(i     j     k)\omega_p\cdot\omega_p Y}$$
より
　$${Y=(i     j     k)(\omega_p)^2 Y}$$
上記と同じ計算を繰り返すことにより
　$${Y=(\omega_p)^2\{(i     j     k)Y\}}$$
　$${Y=(\omega_p)^2\cdot\omega_p Y}$$
　$${Y=(\omega_p)^3 Y}$$
この式が成り立つためには
　$${(\omega_p)^{\underline{3}}=1    \cdots ⑩}$$
すると $${\omega_p}$$ は、$${⑦,   ⑧}$$ の条件
　$${(\omega_p)^{\underline{p}}=1    \cdots ⑦}$$
かつ
　$${\omega_p\ne1    \cdots ⑧}$$
を満たす定数なので、$${⑦}$$ と $${⑩}$$ との指数部分（下線部）の比較で $${p=3}$$ と決定し、$${⑦,   ⑧}$$ について $${p=3}$$ として
　$${(\omega_3)^3=1}$$
かつ
　$${\omega_3\ne1}$$
となります。つまり $${\omega_3}$$ は「$${3}$$ 乗して $${1}$$ になる数（$${1}$$ の $${3}$$ 乗恨）のうち、$${1}$$ ではない数」となるので、 $${\omega_3=1}$$ は却下されて
　$${\omega_3=\omega,  \omega^2}$$
となり、これを $${⑥}$$ 式
　$${Y'=\omega_p Y    \cdots ⑥}$$
に代入して
　$${Y'=\omega Y,  \omega^2 Y}$$
さらに、これに $${①}$$ 式
　$${(i     j     k)Y=Y'\,(\ne Y)　\cdots ①}$$
を代入して
　$${(i     j     k)Y=\omega Y,  \omega^2Y}$$
となり、これは本文中の $${④}$$ 式
　$${(i     j     k)Y=\omega Y,  \omega^2Y　\cdots ④}$$
とまったく同じ式となります。この（注３）でおこなった $${p}$$ を求める証明は、初めから $${p=3}$$ を前提にしている本文より厳密な証明となっています（本文全体の整合性を整える必要があるので、この注は、全体の執筆後に本文の方に移行する予定。）。

（注４）３次の遇置換をラグランジュ・リゾルベントに作用させる（復習）

　次の「条件Ⅱ」

「条件Ⅱ」
　『$${Y}$$ はある遇置換で変化するが、$${Y^3}$$ はすべての遇置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は遇置換で対称性が壊れているが、$${Y^3}$$ は遇置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

または、『すべての遇置換は３次巡回置換で表すことができる』ことから遇置換を３次巡回置換に置き換えた

「条件Ⅱ」（３次巡回置換バージョン）
　『$${Y}$$ はある３次巡回置換で変化するが、$${Y^3}$$ はすべての３次巡回置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は３次巡回置換で対称性が壊れているが、$${Y^3}$$ は３次巡回置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

をみたす式 $${Y}$$ は、３次方程式においてはラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
となります。このことを確認しておきます（$${\Rightarrow}$$ 本シリーズ (13) 参照）。
　なお $${\alpha,  \beta,  \gamma}$$ は３次方程式 $${ax^2+bx^2+cx+d=0}$$ の解です。その解で得られる３次置換は、次のように全部で６通りありました。

$$
\begin{align*}
&\begin{rcases}
(1)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
(2)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
(3)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}遇置換\\
\\
&\begin{rcases}
(4)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
(5)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
(6)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

$${(1)}$$～$${(3)}$$ は偶数個の互換の積で表せるので遇置換、$${(4)}$$～$${(6)}$$ は奇数個の互換の積で表せるので奇置換となります。すると遇置換は必ず３次巡回置換で表すことができるので、$${(1)}$$～$${(3)}$$ は次のように表せます。

$$
\begin{align*}
&\begin{rcases}
(1)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)\\
\\
(2)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
(3)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
(4)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
(5)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
(6)\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

確認ですが、$${(1)}$$ は同じ３次巡回置換を連続３回作用させると元に戻る（変化しない）ということです。$${(2)}$$ は
　$${\alpha\rightarrow\gamma\rightarrow\beta\rightarrow\alpha\rightarrow\cdots}$$
と巡回する置換なので $${(\alpha     \gamma     \beta)}$$ と表すことができ、$${(3)}$$ は
　$${\alpha\rightarrow\beta\rightarrow\gamma\rightarrow\alpha\rightarrow\cdots}$$
と巡回する置換なので $${(\alpha     \beta     \gamma)}$$ と表すことができます。
　さて復習として、このラグランジュ・リゾルベント $${A}$$ に、$${(2)}$$ と $${(3)}$$ の２つの３次巡回置換

$${(2)}$$　$${\dbinom{\alpha       \beta       \gamma}{\gamma       \alpha       \beta}=(\alpha     \gamma     \beta)}$$

$${(3)}$$　$${\dbinom{\alpha       \beta       \gamma}{\beta       \gamma       \alpha}=(\alpha     \beta     \gamma)}$$

を作用させて、どちらにおいても「条件Ⅱ」を満たしていることを確認してみます。

$${(2)}$$ $${(\alpha     \gamma     \beta)}$$ を $${A}$$ に作用させる。
　$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に
　$${\alpha \rightarrow \gamma \rightarrow \beta \rightarrow \alpha}$$
と巡回的に置き換えると

$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow\\
&\gamma+\omega\alpha+\omega^2\beta\\
=\,&\underset{1}{\underline{\omega^3}}\,\gamma+\omega\alpha+\omega^2\beta\\
=\,&\omega(\omega^2\gamma+\alpha+\omega\beta)\\
=\,&\omega(\alpha+\omega\beta+\omega^2\gamma)\\
=\,&\omega A
\end{align*}
$$

より
　$${(\alpha     \gamma     \beta)A=\omega A　\cdots ⑫}$$
となり、$${A}$$ は $${\omega A}$$ に変化します。
　所々で $${\omega^3=1}$$ をうまく使います。$${\gamma}$$ に $${\omega^3}$$ をかけるのがポイントです。$${\omega^3}$$ は $${1}$$ なので掛けても式の値は変わりません。また最後に $${\omega}$$ でくくって $${\omega A}$$ を導いています。$${\omega}$$ でくくったときに、$${\alpha}$$ の係数が $${1}$$ になるようにするのもポイントです。
　また、$${(\alpha     \gamma     \beta)}$$ の $${A^3}$$ への作用は、$${A}$$ のみに作用して３乗は変えないので

$$
\begin{align*}
(\alpha     \gamma     \beta)A^3&=(\alpha     \gamma     \beta)A\cdot(\alpha     \gamma     \beta)A\cdot(\alpha     \gamma     \beta)A\\
&=\{(\alpha     \gamma     \beta)A\}^3\\
&=(\omega A)^3　　（ ⑫ を代入）\\
&=\omega^3A^3
\end{align*}
$$

$${\omega^3=1}$$ より

$$
\begin{align*}
(\alpha     \gamma     \beta)A^3&=A^3\\
\end{align*}
$$

となり、$${A^3}$$ は変化しません。これで確かにラグランジュ・リゾルベント $${A}$$ は「条件Ⅱ」の $${Y}$$

「条件Ⅱ」（３次巡回置換バージョン）
　『$${Y}$$ はある３次巡回置換で変化するが、$${Y^3}$$ はすべての３次巡回置換で変化しない（ただし $${Y^3}$$ は対称式ではない）』
　言い換えると
　『$${Y}$$ は３次巡回置換で対称性が壊れているが、$${Y^3}$$ は３次巡回置換で対称性が保たれている（ただし $${Y^3}$$ は対称式ではない）』

を満たします。$${Y}$$ として
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$ 
をとればいいわけです。次に (3) を作用させてみます。

$${(3)}$$ $${(\alpha     \beta     \gamma)}$$ を $${A}$$ に作用させる。
　$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に
　$${\alpha \rightarrow \beta \rightarrow \gamma \rightarrow \alpha}$$
と巡回的に置き換えると

$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow\\
&\beta+\omega\gamma+\omega^2\alpha\\
=\,&\underset{1}{\underline{\omega^3}}\,\beta+\underset{1}{\underline{\omega^3}}\cdot\omega\gamma+\omega^2\alpha\\
=\,&\omega^3\beta+\omega^4\gamma+\omega^2\alpha\\
=\,&\omega^2(\omega\beta+\omega^2\gamma+\alpha)\\
=\,&\omega^2(\alpha+\omega\beta+\omega^2\gamma)=\omega^2A\\
\end{align*}
$$

より
　$${(\alpha     \beta     \gamma)A=\omega^2A　\cdots ⑬}$$
となり、$${A}$$ は $${\omega^2A}$$ に変化します。
　ここでも所々で $${\omega^3=1}$$ を使います。$${\omega^3}$$ は $${1}$$ なので掛けても式の値は変わりません。また最後に $${\omega^2}$$ でくくって $${\omega^2A}$$ を導きます。ここでも $${\omega^2}$$ でくくったときに、$${\alpha}$$ の係数が $${1}$$ になるようにするのがポイントです。
　また、$${(\alpha     \gamma     \beta)}$$ の $${A^3}$$ への作用は、$${A}$$ のみに作用して３乗は変えないので

$$
\begin{align*}
(\alpha     \beta     \gamma)A^3&=(\alpha     \beta     \gamma)A\cdot(\alpha     \beta     \gamma)A\cdot(\alpha     \beta     \gamma)A\\
&=\{(\alpha     \beta     \gamma)A\}^3\\
&=\{\omega^2A\}^3　　（⑬を代入）\\
&=(\omega^2)^3A^3\\
&=\omega^6A^3
\end{align*}
$$

$${\omega^6=(\omega^3)^2=2^2=1}$$ より

$$
\begin{align*}
(\alpha     \gamma     \beta)A^3&=A^3\\
\end{align*}
$$

となり、$${A^3}$$ は変化しません。(2)と同様、 (3) のときも確かに $${A}$$ は「条件Ⅱ」の $${Y}$$ を満たします。
　これで「条件Ⅱ」を満たす $${Y}$$ として、ラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
をとってもよいことがわかりました。

（注５）ラグランジュ・リゾルベントは対称式ではないこと

　$${A^3}$$ に互換 $${(\alpha     \beta)}$$ を作用させる。つまり $${A^3}$$ について $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換えると

$$
\begin{align*}
A^3=\,&(\alpha+\omega\beta+\omega^2\gamma)^3\\
&\hspace{2pt}\downarrow\hspace{20pt}\downarrow\\
&(\beta+\omega\alpha+\omega^2\gamma)^3 \ne A^3 
\end{align*}
$$

となり別の式になります。

（注６）「すくなくとも１つ」の意味

　『$${Y}$$ は３次巡回置換で変化する』という条件を満たためには、その３次巡回置換は「少なくとも１つ」存在すればいいのですが、もちろん複数あっても構いません。なお、まったく存在しないのは『$${Y}$$ は３次巡回置換で変化する』という条件をそもそも満たさないので論外となります。
　実際、３次方程式の解の公式では、$${Y}$$ をラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
とすることによって、２つの３次巡回置換 $${(\alpha     \gamma     \beta)}$$ と $${(\alpha     \beta     \gamma)}$$ で変化しました（注４）。

（注７）式に置換を作用させるときの表記法（復習）

　ある式 $${A}$$ に例えば置換 $${\dbinom{\alpha       \beta       \gamma}{\beta       \gamma       \alpha}}$$ を作用させることを、次のように表記します。

$$
\begin{align*}
&\dbinom{\alpha       \beta       \gamma}{\beta       \gamma       \alpha}A\\
&\hspace{21pt}\uparrow\hspace{26pt}\uparrow\\
&\hspace{17pt}{\small 置換}\hspace{17pt}{\small 式}
\end{align*}
$$

つまり、式の前に作用させたい置換を置きます。今の場合、この置換は

$$
\begin{align*}
\dbinom{\alpha       \beta       \gamma}{\beta       \gamma       \alpha}
=(\alpha     \beta     \gamma)
\end{align*}
$$

と巡回置換で書けたので、次のように簡潔に表記できます。

$$
\begin{align*}
&(\alpha     \beta     \gamma)A\\
&\hspace{16pt}\uparrow\hspace{19pt}\uparrow\\
&\hspace{12pt}{\small 置換}\hspace{11pt}{\small 式}
\end{align*}
$$

例えば、差積 $${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ に巡回置換 $${(\alpha     \beta     \gamma)}$$ を作用させることは次のように表記できます。

$$
\begin{align*}
&(\alpha     \beta     \gamma)X_3\\
=\,&(\alpha     \beta     \gamma)\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}\\
&\hspace{16pt}\uparrow\hspace{69pt}\uparrow\\
&\hspace{12pt}{\small 置換}\hspace{61pt}{\small 式}
\end{align*}
$$

式は３つの小カッコ $${(\hspace{14pt})(\hspace{14pt})(\hspace{14pt})}$$ で構成されるので、外側を中カッコ $${\{\hspace{14pt}\}}$$ で囲います。小カッコの外は中カッコで囲うルールです。さて復習も兼ねて実際にこの置換を実行すると、３次巡回置換 $${(\alpha     \beta     \gamma)}$$ は
　$${\alpha \rightarrow \beta \rightarrow \gamma \rightarrow \alpha}$$
と $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に巡回的に置き換えるので

$$
\begin{align*}
(\alpha     \beta     \gamma)\{&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}\\
&\hspace{1.5pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow \hspace{9pt}\downarrow\hspace{13pt}\downarrow\\
=\,&(\gamma-\alpha)(\alpha-\beta)(\beta-\gamma)\\
=\,&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\hspace{2pt}\Leftarrow 変化しない
\end{align*}
$$

となり、式は変化しないことがわかります。

（注８）３乗の方程式を解くことについて

　本文でも書きましたが
　$${\{(i     j     k)Y\}^3=Y^3　\cdots (*1)}$$
から $${(i     j     k)Y}$$ を決定すると、一時的に
　$${(i     j     k)Y=Y,  \omega Y,  \omega^2Y}$$　
となりますが、本文 $${①}$$ より $${(i     j     k)Y\ne Y}$$ なので、$${Y}$$ は却下されて
　$${(i     j     k)Y=\omega Y,  \omega^2Y　\cdots (*2)}$$
となることは本文で述べました。$${(i     j     k)Y}$$ は、$${Y}$$ の $${\omega}$$ 倍か、$${\omega^2}$$ 倍と決定されます。なお $${\omega}$$ は、「$${3}$$ 乗して $${1}$$ になる数（$${1}$$ の $${3}$$ 乗恨 $${1,  \omega,  \omega^2}$$）のうち $${1}$$ ではない数」です。具体的には虚数
　$${\omega=\dfrac{1+\sqrt{3}i}{2}}$$
または
　$${\omega=\dfrac{1-\sqrt{3}i}{2}}$$
となります。これと同様の議論は、高校数学では

 問題　$${x^3=27}$$ を解きなさい。ただし $${x}$$ は複素数とする。

というような問題で現れます。具体的に解いてみると、与式を $${27}$$ で割って
　$${\dfrac{x^3}{27}=1}$$
$${27=3^3}$$ より
　$${\dfrac{x^3}{3^3}=1}$$　$${\left(\dfrac{x}{3}\right)^3=1}$$
より、３乗して $${1}$$ になる数は $${1,  \omega,  \omega^2}$$ なので
　$${\dfrac{x}{3}=1,  \omega,  \omega^2}$$
両辺に $${3}$$ をかけて
　$${x=3,  3\omega,  3\omega^2}$$
として解が得られます。$${x^3=27}$$ をみたす解は、$${3}$$ は自明ですが、他にも $${3}$$ の $${\omega}$$ 倍と、$${3}$$ の $${\omega^2}$$ 倍というように、３つの解
　$${x=3,  3\omega,  3\omega^2}$$
があるということです。このことは次のような形式で知っておくとよいでしょう。

＜$${\boldsymbol{x^3=a}}$$ の解＞
 $${a}$$ を実数として $${x^3=a}$$ の解は
　$${x=\sqrt[3]{a},  \sqrt[3]{a}\,\omega,  \sqrt[3]{a}\,\omega^2}$$
なお $${\omega}$$ は、「$${3}$$ 乗して $${1}$$ になる数（$${1}$$ の $${3}$$ 乗恨 $${1,  \omega,  \omega^2}$$）のうち $${1}$$ ではない数」 。具体的には虚数
　$${\omega=\dfrac{1+\sqrt{3}i}{2}}$$
または
　$${\dfrac{1-\sqrt{3}i}{2}}$$
である。

　例えば、$${x^3=5}$$ の解は
　$${x=\sqrt[3]{5},  \sqrt[3]{5}\,\omega,  \sqrt[3]{5}\,\omega^2}$$
$${x^3=8}$$ の解は
　$${x=\sqrt[3]{8},  \sqrt[3]{8}\,\omega,  \sqrt[3]{8}\,\omega^2}$$
ここで $${\sqrt[3]{8}=\sqrt[3]{2^3}=2}$$ より
　$${x=2,  2\omega,  2\omega^2}$$
となります。最初の
　$${\{(i     j     k)Y\}^3=Y^3　\cdots (*1)}$$
から
　$${(i     j     k)Y=\omega Y,  \omega^2Y　\cdots (*2)}$$
と決定する過程も、この形式にのっとっています。（蛇足ですが）このことを分かりよくするために $${(i     j     k)Y}$$ を $${X}$$ と置いてみます。すると $${(*1)}$$ は
　$${X^3=Y^3}$$
ここで、上で述べた $${x^3=a}$$ の解の形式を使って
　$${X=\sqrt[3]{Y^3},  \omega\sqrt[3]{Y^3},  \omega^2\sqrt[3]{Y^3}}$$
$${\sqrt[3]{Y^3}=Y}$$ より 
　$${X=Y,  \omega Y,  \omega^2 Y}$$
ここで、$${X}$$ を $${(i     j     k)Y}$$ に戻して
　$${(i     j     k)Y=Y,  \omega Y,  \omega^2Y}$$
本文 $${①}$$ より $${(i     j     k)Y\ne Y}$$ なので
　$${(i     j     k)Y=\omega Y,  \omega^2Y　\cdots (*2)}$$
と $${(i     j     k)Y}$$ は決定されます。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となることを解説
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（破壊する）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（破壊する）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説（１編）。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説（２編）。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説（３編）。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）（予定）「アーベルの証明」の解説（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。