
偶置換と奇置換について
竹村の家庭教師が始まった。
「前回は3次方程式の解の公式を『解の置換』と『対称式』という観点で導出した。今日はその『解の置換』について理解を深めていこうと思う。このことが、5次以上の方程式に解の公式が存在しないことの鍵となっていくよ。まずは、何度も出てきた3次方程式の3つの解の置換を確認しておこう」
「はい!」小学5年生の森田君の声が家中に響いた。
<3つの解 $${\boldsymbol{\alpha, \beta, \gamma}}$$ の置換(復習)>
➀ $${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に、$${\gamma}$$ を $${\gamma}$$ に、つまりそのままで変わらない置換、すなわち
$$
\begin{align*}
\alpha\longrightarrow \alpha\\
\beta\longrightarrow \beta\\
\gamma\longrightarrow \gamma
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
$$
② $${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換、すなわち
$$
\begin{align*}
\alpha\longrightarrow\gamma\\
\beta\longrightarrow\alpha\\
\gamma\longrightarrow\beta
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
$$
③ $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換、すなわち
$$
\begin{align*}
\alpha\longrightarrow \beta\\
\beta\longrightarrow \gamma\\
\gamma\longrightarrow \alpha
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
$$
④ $${\alpha}$$ はそのままで、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換、すなわち
$$
\begin{align*}
\alpha\longrightarrow\alpha\\
\beta\longrightarrow\gamma\\
\gamma\longrightarrow\beta
\end{align*}
\hspace{14pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
$$
➄ $${\alpha}$$ を $${\gamma}$$ に、$${\beta}$$ はそのままで、$${\gamma}$$ を $${\alpha}$$ に置き換える置換、すなわち
$$
\begin{align*}
\alpha\longrightarrow\gamma\\
\beta\longrightarrow\beta\\
\gamma\longrightarrow\alpha
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
$$
⑥ $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に、$${\gamma}$$ は変化しない置換、すなわち
$$
\begin{align*}
\alpha\longrightarrow\beta\\
\beta\longrightarrow\alpha\\
\gamma\longrightarrow\gamma
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
$$
( )の中の文字は、上から下に置換される、と見ればいいね。あと3つの解の置換はこの6つがすべてで、他には無いことも既に習ったね。
さて、ここで3次置換について新しい見方を提示しよう。
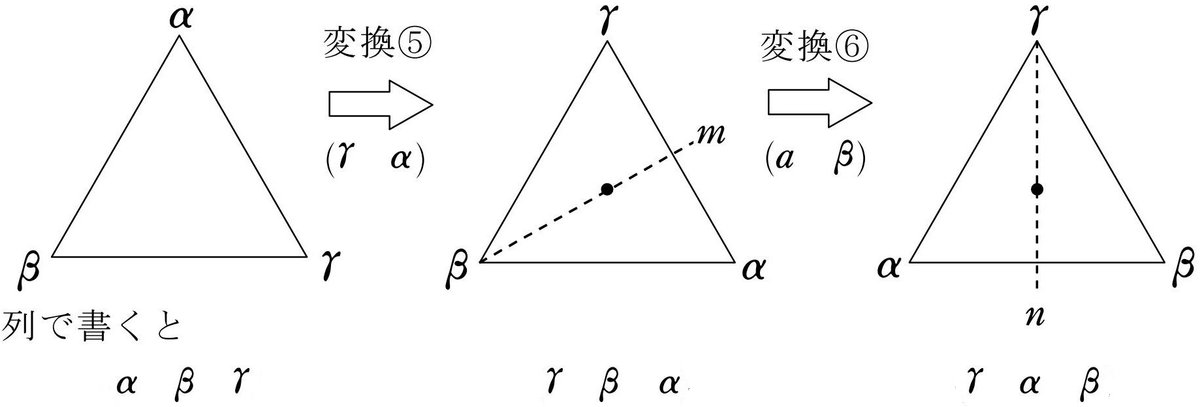
それぞれの置換は、以下のように3角形の「回転」、及び「反転」と、視覚的に理解することができるんだ。
<3つの解の置換を3角形の回転、及び反転でとらえる>
➀ $${\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}}$$ は何も変化しない、つまり回転しない置換。

回転しない操作も「$${0°}$$ 回転の置換」として考える。このように何も変化しない置換を『恒等置換』というんだったね。
② $${\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}}$$は、下図のように反時計回りに $${120°}$$ 回転する置換と見ればわかりやすい。時計回りに $${240°}$$ 回転と見ることもできるが、ここでは反時計回りで統一しよう。

$${120^\circ}$$ 回転によって、$${\alpha}$$ の地点に $${\gamma}$$ が配置され、$${\gamma}$$ の地点に $${\beta}$$ が配置され、$${\beta}$$ の地点に $${\alpha}$$ が配置されるとみると、これは $${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える回転と見ることができる。
$${\alpha → \gamma → \beta → \alpha}$$ と巡回する置換なので、これを『巡回置換』というんだったね。
③ $${\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}}$$ は、下図のように反時計回りに $${240°}$$ 回転する置換と見ればわかりやすい。時計回りに $${120°}$$ 回転と見ることもできるが、ここでも反時計回りで統一する。

$${240^\circ}$$ 回転によって、$${\alpha}$$ の地点に $${\beta}$$ が配置され、$${\beta}$$ の地点に $${\gamma}$$ が配置され、$${\gamma}$$ の地点に $${\alpha}$$ が配置されるとみると、これは $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える回転と見ることができる。
$${\alpha → \beta → \gamma → \alpha}$$ と巡回する置換なので、これも巡回置換になるね。
④ $${\dbinom{\alpha \beta \gamma}{\alpha \gamma \alpha}}$$ は、下図のように $${\alpha}$$ を通る対称軸 $${l}$$ についての反転。

反転によって、$${\beta}$$ の地点に $${\gamma}$$ が配置され、$${\gamma}$$ の地点に $${\beta}$$ が配置される。これは、$${\alpha}$$ はそのままで、$${\beta}$$ と $${\gamma}$$ を入れ替える置換なので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$
と簡単に表すことがある。この $${(\beta \gamma)}$$ を「互いに交換する」という意味で『互換』という。より簡潔な表記で分かりやすくなるね。なお、互換は”2つの解の巡回置換”と見ることもできるね。
➄ $${\dbinom{\alpha \beta \gamma}{\gamma \beta \alpha}}$$ は、下図のように $${\beta}$$ を通る対称軸 $${m}$$ についての反転。

反転によって、$${\alpha}$$ の地点に $${\gamma}$$ が配置され、$${\gamma}$$ の地点に $${\alpha}$$ が配置される。これは $${\beta}$$ はそのままで、$${\alpha}$$ と $${\gamma}$$ を入れ替える置換なので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}
$$
と、これも互換で表すことがある。
⑥ $${\dbinom{\alpha \beta \gamma}{\beta \alpha \gamma}}$$ は、下図のように $${\gamma}$$ を通る対称軸 $${n}$$ についての反転。

反転によって、$${\alpha}$$ の地点に $${\beta}$$ が配置され、$${\beta}$$ の地点に $${\alpha}$$ が配置される。これは $${\gamma}$$ はそのままで、$${\alpha}$$ と $${\beta}$$ を入れ替える置換なので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$
と、これも互換で表すことがある。すると、互換の表記を用いることによって恒等置換➀と、巡回置換②、③についても互換で表すこと、正確に言うと「互角の積」で表すことができるんだ。以下それを示そう。
<恒等置換と巡回置換を互換の積で表す>
① $${\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}}$$ は、下図のように $${\alpha}$$ と $${\beta}$$ の入れ替えの後、再び $${\alpha}$$ と $${\beta}$$ の入れ替えで①と同じ置換となる。

$${(\alpha \beta)}$$ を作用させてから、再び同じ $${(\alpha \beta)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$
と互換の積で表せる。なお、この表し方は1通りではなく、これも含めて以下のように3通りの方法で表すことができるよ。
$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\end{align*}
$$
同じ入れ換えを2回連続で行っているので、もとに戻るのは当たり前だけど、こういうケースも考える。
② $${\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}}$$ は、下図のように $${\beta}$$ と $${\gamma}$$ の入れ替えの後、$${\gamma}$$ と $${\alpha}$$ の入れ替えで②と同じ置換となる。
(Case②-1)

先に $${(\beta \gamma)}$$ を作用させてから、次に $${(\gamma \alpha)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
$$
と互換の積で表せる。なお互換の順番は、先に前の $${(\beta \gamma)}$$ を作用させてから、次に $${(\gamma \alpha)}$$ を作用させると、左から順に作用させていくと定義する。つまり
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\underrightarrow{\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}}
$$
と矢印の順、前から作用させるということだね。テキストによっては後ろからと逆に定義している場合もあるので注意しよう。そのテキストにおいて一貫していれば問題ないね。なお、先ほどやった恒等置換と同じように、互換の積はこの1通りではなく、他にも2通りがある。
(Case②-2) 下図のように、$${\gamma}$$ と $${\alpha}$$ の入れ替えの後、$${\alpha}$$ と $${\beta}$$ の入れ替えで②と同じ置換となる。
先に $${(\gamma \alpha)}$$ を作用させてから、次に $${(\alpha \beta)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$
と互換の積で表せる。3通り目は
(Case②-3) 下図のように、$${\alpha}$$ と $${\beta}$$ の入れ替えの後、$${\beta}$$ と $${\gamma}$$ の入れ替えで②と同じ置換となる。

先に $${(\alpha \beta)}$$ を作用させてから、次に $${(\beta \gamma)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$
と互換の積で表せる。まとめると②の置換は
$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\end{align*}
$$
と、3通りの互換の積で表すことができるね。
③ $${\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}}$$ も、3通りの互換の積で表すことができる。
(Case③-1) 下図のように、$${\beta}$$ と $${\gamma}$$ の入れ替えの後、$${\alpha}$$ と $${\beta}$$ の入れ替えで③と同じ置換となる。

先に $${(\beta \gamma)}$$ を作用させてから、 次に $${(\alpha \beta)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$
(Case③-2) 下図のように、$${\gamma}$$ と $${\alpha}$$ の入れ替えの後、$${\beta}$$ と $${\gamma}$$ の入れ替えで③と同じ置換となる。

先に $${(\gamma \alpha)}$$ を作用させてから、次に $${(\beta \gamma)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$
(Case③-3) 下図のように、$${\alpha}$$ と $${\beta}$$ の入れ替えの後、$${\gamma}$$ と $${\alpha}$$ の入れ替えで③と同じ置換となる。

先に $${(\alpha \beta)}$$ を作用させてから、次に $${(\gamma \alpha)}$$ を作用させるので
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
$$
まとめると③の置換は
$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\end{align*}
$$
以下、すべての互換表示をまとめておこう。
<3つの解の置換のすべての互換表示>
➀について
$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\end{align*}
$$
②について
$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\end{align*}
$$
③について
$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\end{align*}
$$
④について
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$
⑤について
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}
$$
⑥について
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$
すると、ここから見えてくるのは。①の $${0°}$$ 回転も含めて、①、②、③の三角形の回転を表す置換は2つの互換の積で表せる。一方、④~➅のような3角形の反転を表すような置換は1つの互換で表せる、ということだね。
ここで用語の定義をしよう。2つ、4つなど、偶数個の互換で表せる置換を『偶置換』、1つ、3つなど、奇数個の互換の積で表せる置換を『奇置換』という。何も変化しない恒等置換は2つの互換の積で表されるので偶置換だね。
なお、これまでやってきた $${\alpha, \beta, \gamma}$$ の置換を考えるにあたって、$${\alpha, \beta, \gamma}$$ は方程式の解に限定せず、ただの「文字」として考えてもよいことに注意しよう。2つの「文字」 $${\alpha, \beta}$$ の置換を2次置換、3つの「文字」 $${\alpha, \beta, \gamma}$$ の置換を3次置換、一般に、$${n}$$ 個の「文字」の置換を『$${\boldsymbol{n}}$$ 次置換』という。もちろん2次方程式の解 $${\alpha, \beta}$$ の置換は2次置換であるし、3次方程式の解 $${\alpha, \beta, \gamma}$$ の置換は3次置換である。ここで $${n}$$ 次置換について、一般に次のような定理が成り立っているよ。
<『$${\boldsymbol{n}}$$ 次置換』についての定理>
(定理Ⅰ)すべての $${n}$$ 次置換は、1つの互換、または複数の互換の積で表すことができる。
例えば先ほどの3次置換①~➅について、①~③は2つの互換の積、④~⑥は1つの互換で表される。
(定理Ⅱ)ある $${n}$$ 次置換について、その置換が偶置換になるか、奇置換になるかはあらかじめ決まっている。つまり、ある $${n}$$ 次置換が、互換の選び方によって偶置換になったり奇置換になったりすることはない。
例えば先ほどの3次置換①~➅について、①~③は必ず偶置換で奇置換になることはなく、④~➅は必ず奇置換で偶置換になることはない。なお、①~③は複数ある互換の積のうち、代表で1つの互換の積を選んでいるよ。
$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}偶置換\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$
(定理Ⅲ)$${n}$$ 次置換について、偶置換と奇置換に分けたときに、そのときの偶置換と奇置換の個数はもとの置換の2分の1で、互いに同じ個数となる。
例えば先ほどの6つの3次置換について、偶置換は①~③の3つ、奇置換は④~➅の3つで、ちょうど半分ずつ、同じ数ずつ振り分けられることになる。偶置換が4つ、奇置換が2つのようにはならず、偶置換と奇置換の個数はきっちりと半分ずつに分かれるんだ。
$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}3通り\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}3通り
\end{align*}
$$
ちなみに、$${\alpha, \beta}$$ による2次置換は
$$
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
\hspace{10pt}と\hspace{10pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha\
\end{pmatrix}
$$
の2通りだけど、これらも
$$
\begin{align*}
&\begin{rcases}
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}偶置換\\
\\
&\begin{rcases}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$
と、偶置換と奇置換で1個ずつ同じ数になるね。では、今日の授業はここまで。この偶置換と奇置換を考えることによって、5次以上の方程式には解の公式が存在しないことが・・・」
「先生!」じっと聴いていた森田君の声が響いた。
「分かりそうなので、いったん整理してみてもよろしいでしょうか」
「整理?そうだね、整理してみよう」
「分かりました」
森田君はホワイトボードの前に立ち、親指だけで黒マーカーのキャップをカチッと開けた。
「まず2次方程式の解の公式は、2次方程式のラグランジュ・リゾルベント
$$
\begin{align*}
&\alpha+\beta\\
&\alpha-\beta
\end{align*}
$$
を足したものと引いたものを、2で割った以下の恒等式から始まりました。恒等式とは恒に成り立つ式のことでした。
$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}
\end{align*}
$$
すると $${\alpha+\beta}$$ は、$${\alpha}$$ と $${\beta}$$ を入れ替えても式が変わらない ので対称式、とりわけ基本対称式となります。
$$
\begin{align*}
\alpha+\beta \longrightarrow\,\,&\beta+\alpha\\
=\,\,&\alpha+\beta
\end{align*}
$$
よって2次方程式 $${ax^2+bx+cx=0}$$ の解と係数の関係
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
の1つ目より、 $${\alpha+\beta}$$ は $${\dfrac{c}{a}}$$ と、2次方程式の係数 $${a, b, c}$$ で表すことができます。解と係数の関係の左辺は基本対称式$${\alpha+\beta, \alpha\beta}$$ でした。
$$
\begin{align*}
\underset{\scriptsize 基本対称式}{\alpha+\beta}&=-\dfrac{b}{a}\\
\underset{\scriptsize 基本対称式}{\alpha\beta}&=\dfrac{c}{a}
\end{align*}
$$
しかし $${\alpha-\beta}$$ は、$${\alpha}$$ と $${\beta}$$ を入れ替えると
$$
\begin{align*}
\alpha-\beta \longrightarrow\,\,&\beta-\alpha\\
=&-\alpha+\beta\\
=&-(\alpha-\beta)
\end{align*}
$$
と $${-1}$$ 倍となって式が変わってしまうので、対称式ではありません。つまり
$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}
\end{align*}
$$
は、このままでは2次方程式の係数 $${a, b, c}$$ で表すことは不可能です。$${\alpha-\beta}$$ が対称式ではないからです。「対称式の基本定理」より、対称式でなければ基本対称式 $${\alpha+\beta, \alpha\beta}$$ の加減乗除、つまり足し算・引き算・掛け算・割り算で表すことができません。
<対称式の基本定理(復習)>
対称式である $${\longleftrightarrow}$$ 基本対称式の加減乗除で表すことができる。
対称式でない $${\longleftrightarrow}$$ 基本対称式の加減乗除で表すことができない。
基本対称式の加減乗除で表すことができなければ、解と係数の関係
$$
\begin{align*}
\underset{\scriptsize 基本対称式}{\alpha+\beta}&=-\dfrac{b}{a}\\
\underset{\scriptsize 基本対称式}{\alpha\beta}&=\dfrac{c}{a}
\end{align*}
$$
を用いて、2次方程式の係数 $$[a, b, c}$$ の加減乗除で表すことはできないわけです。
$$
\begin{align*}
\alpha-\beta &\longrightarrow 対称式ではない\\
&\longrightarrow 基本対称式 \alpha+\beta, \alpha\beta の加減乗除で表せない\\
&\longrightarrow 解と係数の関係を用いて係数の加減乗除で表せない
\end{align*}
$$
そもそも解の公式とは「解をその方程式の係数で表すこと」なので、係数で表せなければすでに破綻です。しかし $${\alpha-\beta}$$ の2乗 $${(\alpha-\beta)^2}$$ は、$${\alpha}$$ と $${\beta}$$ を入れ替えても
$$
\begin{align*}
(\alpha-\beta)^2 \longrightarrow\,\,&(\beta-\alpha)^2\\
=\,\,&(-\alpha+\beta)^2\\
=\,\,&\{-(\alpha-\beta)\}^2\\
=\,\,&(\alpha-\beta)^2
\end{align*}
$$
と変化しないので対称式になります。$${-1}$$ 倍は2乗すると $${1}$$ 倍になるからです。すると、対称式は基本対称式の加減乗除で表せることより、$${(\alpha-\beta)^2}$$ は
$$
\begin{align*}
(\alpha-\beta)^2&=\alpha^2-2\alpha\beta+\beta^2\\
&=(\alpha+\beta)^2-4\alpha\beta
\end{align*}
$$
と基本対称式 $${\alpha+\beta, \alpha\beta}$$ で表現できるので、これに、2次方程式の解と係数の関係
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
を代入することによって
$$
\begin{align*}
(\alpha-\beta)^2&=(\alpha+\beta)^2-4\alpha\beta\\
&=\left(-\dfrac{b}{a}\right)^2-4\left(\dfrac{c}{a}\right)\\
&=\dfrac{b^2}{a^2}-\dfrac{4c}{a}\\
&=\dfrac{b^2}{a^2}-\dfrac{4ac}{a^2}\\
&=\dfrac{b^2-4ac}{a^2}
\end{align*}
$$
と、2次方程式の係数 $${a, b, c}$$ の加減乗除で表せます。すると、この式の平方根、つまりルートを取ることによって
$$
\begin{align*}
\alpha-\beta=\pm\sqrt{\dfrac{b^2-4ac}{a^2}}
\end{align*}
$$
と $${\alpha-\beta}$$ を平方根を用いて表すことができました。加減乗除だけでは不可能でしたが、"平方根"という新しい演算を用いることによって係数 $${a, b, c}$$ で表すことが実現できたのです。後は、これと解と係数の関係よりあらかじめわかっていた
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}
\end{align*}
$$
を、解の公式の「種」となる
$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}
\end{align*}
$$
に代入することによって $${\alpha, \beta}$$ を2次方程式の係数で表すことができます。具体的には、$${\alpha-\beta}$$ はプラスとマイナスの2通りがあるので、場合分けをして
(case1) $${\alpha+\beta=-\dfrac{b}{a}, \alpha-\beta=\sqrt{\dfrac{b^2-4ac}{a^2}}}$$ を代入すれば
$$
\begin{align*}
\alpha&=\dfrac{-\dfrac{d}{a}+\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\
\beta&=\dfrac{-\dfrac{d}{a}-\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}
\end{align*}
$$
(case2) $${\alpha+\beta=-\dfrac{b}{a}, \alpha-\beta=-\sqrt{\dfrac{b^2-4ac}{a^2}}}$$ を代入すれば
$$
\begin{align*}
\alpha&=\dfrac{-\dfrac{d}{a}-\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\
\beta&=\dfrac{-\dfrac{d}{a}+\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}
\end{align*}
$$
と、はれて $${\alpha, \beta}$$ を2次方程式の係数 $${a, b, c}$$ を用いて表すことができました。なお $${\alpha}$$ と $${\beta}$$ は、上のようにプラスとマイナスの組み合わせで2組現れますが、$${\alpha}$$ と $${\beta}$$ には区別が無いので、上の2組は全くの対等です。それでこれを ”$${x=}$$” として、プラスマイナス ”$${\pm}$$” の記号を使って1つにまとめた
$$
\begin{align*}
x=\dfrac{-\dfrac{d}{a}-\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}
\end{align*}
$$
が、解の公式となります。後はこれを計算していけば
$$
\begin{align*}
x&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\dfrac{\sqrt{b^2-4ac}}{\sqrt{a^2}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\dfrac{\sqrt{b^2-4ac}}{a}}{2}\\
&=\dfrac{\dfrac{1}{a}\{-b\pm\sqrt{b^2-4ac}\}}{2}\\
&=\dfrac{1}{a}\cdot\dfrac{-b\pm\sqrt{b^2-4ac}}{2}\\
&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$
と2次方程式の解の公式が得られます。
ここで注意しておきたいのは $${\alpha, \beta}$$ は対称式ではないということです。$${\alpha}$$ と $${\beta}$$ の入れ替えによって、$${\alpha}$$ は $${\beta}$$ に、$${\beta}$$ は $${\alpha}$$ に変化します。
$$
\begin{align*}
\alpha &\longrightarrow\beta\\
\beta &\longrightarrow\alpha
\end{align*}
$$
$${\alpha, \beta}$$ は対称式ではないので、基本対称式の加減乗除で表すことはできません。しかし解の公式を得るためには「$${\alpha, \beta}$$ を基本対称式で表す」必要があります。何度も出てきたように、基本対称式で表すことによって、解と係数の関係
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
を利用できるからです。解と係数の関係の左辺は基本対称式、右辺は2次方程式の係数です。つまり解を基本対称式で表すことができれば、それを「解と係数の関係の右辺に置き換える」ことによって2次方程式の係数で表すことができます。それが解の公式に他なりません。では対称式ではない $${\alpha, \beta}$$ を、どうやって基本対称式で表すのか?対称式ではないので、基本対称式の加減乗除だけで表すのは不可能。加減乗除以外の別のアイデアが必要となります。そこで”平方根”、つまりルートを利用します。先ほど導いた
$$
\begin{align*}
(\alpha-\beta)^2=\dfrac{b^2-4ac}{a^2}
\end{align*}
$$
から
$$
\begin{align*}
\alpha-\beta=\pm\sqrt{\dfrac{b^2-4ac}{a^2}}
\end{align*}
$$
と、平方根をとることによって生じる $${\pm}$$ の不定性、つまりプラスかマイナスか定まらない性質を利用することによって、$${\alpha, \beta}$$ の解の入れ替えを $${\pm}$$ の入れ替えへと1対1で対応させることが可能となったのです。
$$
\begin{align*}
&\alpha=\dfrac{-\dfrac{b}{a}+\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\
解の入れ替え\hspace{2pt}&\hspace{-2pt}\updownarrow\hspace{35pt}\updownarrow\pm の入れ替え\\
&\beta=\dfrac{-\dfrac{b}{a}-\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}
\end{align*}
$$
$$
\begin{align*}
&\alpha=\dfrac{-\dfrac{b}{a}-\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\
解の入れ替え\hspace{2pt}&\hspace{-2pt}\updownarrow\hspace{35pt}\updownarrow\pm の入れ替え\\
&\beta=\dfrac{-\dfrac{b}{a}+\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}
\end{align*}
$$
そもそも対称性のない $${\alpha, \beta}$$ を、対称性を崩しながら $${\alpha+\beta}$$ と $${(\alpha-\beta)^2}$$ の対称式を用いて表すことを可能にした。それが平方根を取るといいうアイデアです。対称式ではない $${\alpha-\beta}$$ の2乗 $${(\alpha-\beta)^2}$$ は対称式になりますが、その平方根を取ることによってプラスマイナの不定性を表出させ、$${(\alpha-\beta)^2}$$ の対称性を崩し解の公式を実現させた。「対称性のない式を対称式を用いて表す」というミッションを、平方根を取るという操作によって可能としたのです。
このことをふまえて、3次方程式の解の公式を見てみます。3次方程式の解の公式は次のようになりました」
森田君はまるでひらがなを書くように解の公式を書き進める。
$$
x=
\begin{cases}
-\dfrac{b}{3a}+\sqrt[3]{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}+\sqrt[3]{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}\\
-\dfrac{b}{3 a}+\omega \sqrt[3]{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}+\omega^{2}\sqrt[3]{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}\\
-\dfrac{b}{3 a}+\omega^{2} \sqrt[3]{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}+\omega\sqrt[3]{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}
\end{cases}
$$
ただし
$$
\begin{align*}
p&=-\dfrac{1}{3}\left(\dfrac{b}{a}\right)^{2}+\dfrac{c}{a}\\
q&=\dfrac{2}{27}\left(\dfrac{b}{a}\right)^{3}-\dfrac{1}{3}\left(\dfrac{b}{a}\right)\left(\dfrac{c}{a}\right)+\dfrac{d}{a}
\end{align*}
$$
「3次方程式の解の公式を見ると、3乗根 $${\sqrt[3]{ }}$$ の中に平方根 $${\sqrt{ }}$$ が入っています。ただし、前の3乗恨にはプラス、後ろの3乗根にはマイナスで平方根が入っています」
$$
x=
\begin{cases}
-\dfrac{b}{3a}+\overset{前の3乗根}{\sqrt[3]{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}}
+\overset{後ろの3乗根}{\sqrt[3]{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}}\\[-5pt]
\hspace{53.5pt}\underset{プラス}{\uparrow}\hspace{20pt}{\scriptsize 平方根}\hspace{48pt}\underset{マイナス}{\uparrow}\hspace{15pt}{\scriptsize 平方根}\\[10pt]
-\dfrac{b}{3a}+\omega\overset{前の3乗根}{\sqrt[3]{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}}
+\omega^{2}\overset{後ろの3乗根}{\sqrt[3]{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}}\\[-5pt]
\hspace{60pt}\underset{プラス}{\uparrow}\hspace{19pt}{\scriptsize 平方根}\hspace{59.5pt}\underset{マイナス}{\uparrow}\hspace{15pt}{\scriptsize 平方根}\\[10pt]
-\dfrac{b}{3a}+\omega^{2}\overset{前の3乗根}{\sqrt[3]{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}}
+\omega\overset{後ろの3乗根}{\sqrt[3]{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}}}}\\[-5pt]
\hspace{64pt}\underset{プラス}{\uparrow}\hspace{19pt}{\scriptsize 平方根}\hspace{55pt}\underset{マイナス}{\uparrow}\hspace{15pt}{\scriptsize 平方根}
\end{cases}
$$
「これがどいう意味なのかを考えてみたんです。2次方程式の解の公式では、対称式ではない $${\alpha-\beta}$$ の2乗 $${(\alpha-\beta)^2=\sqrt{\dfrac{b^2-4ac}{a^2}}}$$ は対称式になります。そこで、その平方根を考えました。平方根を取ることによって
$$
\begin{align*}
\alpha-\beta&=\pm\sqrt{\dfrac{b^2-4ac}{a^2}}
\end{align*}
$$
とプラスマイナスの不定性、つまりプラスかマイナスかの決まらない性質を表出させることによって、$${(\alpha-\beta)^2}$$ の対称性を崩し解の公式を実現させました。ということは3次方程式だと・・・」
森田君は右斜め上を見上げた。
「3次方程式だと?」
竹村は同じ言葉でそのまま返す。森田君は口元に手をやる。
「平方根の中身は・・・」
「平方根の中身は?」
「$${\alpha-\beta}$$ の拡張として・・・」
「$${\alpha-\beta}$$ の拡張として?」
「3次方程式の3つの解 $${\alpha, \beta, \gamma}$$ で得られる・・・」
「3つの解 $${\alpha, \beta, \gamma}$$ で得られる?」
「対称式ではないものなので・・・」
「対称式ではないものなので?」
「$${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$。そしてこれは・・・」
「そしてこれは?」
「奇置換では $${-1}$$ 倍に変化しますが・・・」
「変化しますが?」
「2乗すると・・・」
「2乗すると?」
「対称式・・・。先生、できそうです!次の授業までに考えておきます」
「よし、森田君も考えてみて!それでは今日の授業はここまで!」
最後、森田君の核心へ迫っていくような迫力に飲まれそうになった竹村は、ちゃんと予習しようと夜中まで開いている図書館へと向かった。
(了)
(コメント)ひとまず完成というより叩き台です。初めて読んだときの印象がどうなっているのか不明であります。日本語での表現がうまくいっていない感もありますが、気付いたら随時修正中。大きく直す場合もあります。整合性を保つために、過去のシリーズも随時修正しています。(5)は一度非公開にして全面的に直す予定です。
いいなと思ったら応援しよう!

