
(追記あり)中学でも分かる➁「積分法」
前回は微分法を勉強しました。ここでは、その微分の逆演算である積分法を勉強します。
・不定積分
・定積分
を勉強し、最後に
・定積分が囲われた面積になること
を解説します。イングランドの数学者・物理学者、アイザック・ニュートンの発明した微分積分法の積分です。高校の微分積分で習います。
微分の復習
まずは、前回の微分の復習として、演習問題を与えます。
演習問題
次の関数を微分しなさい。
(1) $${\dfrac{1}{2}x^2+1\raisebox{3ex}{ }}$$
(2) $${\dfrac{1}{2}x^2+3\raisebox{3ex}{ }}$$
(3) $${\dfrac{1}{2}x^2+C\raisebox{3ex}{ }}$$($${C}$$ は定数)
(4) $${\dfrac{1}{3}x^3+C\raisebox{3ex}{ }}$$($${C}$$ は定数)
(5) $${\dfrac{1}{4}x^4+C\raisebox{3ex}{ }}$$($${C}$$ は定数)
解答
(1) $${\left(\dfrac{1}{2}x^2+1\right)'=\dfrac{1}{2}(x^2)'+(1)'=\dfrac{1}{\cancel{2}}\cdot\cancel{2}x+0=x}$$
(2) $${\left(\dfrac{1}{2}x^2+3\right)'=\dfrac{1}{2}(x^2)'+(3)'=\dfrac{1}{\cancel{2}}\cdot\cancel{2}x+0=x\raisebox{3ex}{ }}$$
(3) $${\left(\dfrac{1}{2}x^2+C\right)'=\dfrac{1}{2}(x^2)'+(C)'=\dfrac{1}{\cancel{2}}\cdot\cancel{2}x+0=x\raisebox{3ex}{ }}$$
(4) $${\left(\dfrac{1}{3}x^3+C\right)'=\dfrac{1}{3}(x^3)'+(C)'=\dfrac{1}{\cancel{3}}\cdot\cancel{3}x^2+0=x^2\raisebox{3ex}{ }}$$
(5) $${\left(\dfrac{1}{4}x^4+C\right)'=\dfrac{1}{4}(x^4)'+(C)'=\dfrac{1}{\cancel{4}}\cdot\cancel{4}x^3+0=x^3\raisebox{3ex}{ }}$$
(1) と (2) は、微分の結果はどちらも同じ $${x}$$ です。つまり、$${1}$$ や $${3}$$ のような定数は微分すると $${0}$$ になるので、その定数(実数)部分を一般に $${C}$$ と置いても、微分すると $${x}$$ になります。それが (3) の意味するところです。
また、(3)、(4)、(5) の結果を一般化することによって、これからやる不定積分について重要な公式が得られます。
不定積分
微分すると関数 $${f(x)}$$ になるような関数を、$${f(x)}$$ の不定積分といいます。
$$
\begin{align*}
\\[-14pt]
&?\xrightarrow[]{ 微分する } f(x)\\[-4pt]
&\uparrow\\[-4pt]
&\hspace{-20pt}{\footnotesize f(x) の不定積分}
\end{align*}
$$
上図の「?」に入る関数が不定積分です。
また、関数 $${f(x)}$$ の不定積分を求めることを、$${f(x)}$$ を積分するといいます。
$$
\begin{align*}
\\[-14pt]
&\hspace{10pt}\xrightarrow[]{ 微分する}\\[-12.5pt]
&?\hspace{45pt}f(x)\\[-12.5pt]
&\hspace{10pt}\xleftarrow[ 積分する]{}\\[-6pt]
&\hspace{0pt}\uparrow\\[-4pt]
&\hspace{-20pt}{\footnotesize f(x) の不定積分}
\end{align*}
$$
上図のように、微分と積分の関係は、互いに逆の演算となります。
この章では上の不定積分「?」を求めること、つまりいろいろな関数を積分することを勉強します。
例えば、問題 (1), (2) でやったように
$$
\begin{align*}
\left(\dfrac{1}{2}x^2+1\right)'&=x\\
\left(\dfrac{1}{2}x^2+3\right)'&=x\\
\end{align*}
$$
より、$${\dfrac{1}{2}x^2+1}$$、$${\dfrac{1}{2}x^2+3}$$ はどちらも $${x}$$ の不定積分になります。
$$
\begin{align*}
\\[-14pt]
&\hspace{37pt}\xrightarrow[]{ 微分する}\\[-16.5pt]
&\dfrac{1}{2}x^2+1\hspace{48pt}x\\[-16.5pt]
&\hspace{37pt}\xleftarrow[ 積分する]{}\\[-6pt]
&\hspace{18pt}\uparrow\\[-4pt]
&\hspace{1pt}{\footnotesize x の不定積分}
\end{align*}
$$
$$
\begin{align*}
\\[-14pt]
&\hspace{37pt}\xrightarrow[]{ 微分する}\\[-16.5pt]
&\dfrac{1}{2}x^2+3\hspace{48pt}x\\[-16.5pt]
&\hspace{37pt}\xleftarrow[ 積分する]{}\\[-6pt]
&\hspace{18pt}\uparrow\\[-4pt]
&\hspace{1pt}{\footnotesize x の不定積分}
\end{align*}
$$
しかし (3) のように、定数部分を一般に $${C}$$ とおいて微分しても
$$
\begin{align*}
\left(\dfrac{1}{2}x^2+C\right)'&=x
\end{align*}
$$
と $${x}$$ になるので、$${x}$$ の不定積分は一般に、定数 $${C}$$ を用いて
$$
\begin{align*}
\dfrac{1}{2}x^2+C
\end{align*}
$$
と表されます。
$$
\begin{align*}
\\[-14pt]
&\hspace{40pt}\xrightarrow[]{ 微分する}\\[-16.5pt]
&\dfrac{1}{2}x^2+C\hspace{48pt}x\\[-16.5pt]
&\hspace{40pt}\xleftarrow[ 積分する]{}\\[-6pt]
&\hspace{18pt}\uparrow\\[-4pt]
&\hspace{1pt}{\footnotesize x の不定積分}
\end{align*}
$$
これを、積分記号 $${\int}$$ を用いて次のように表します。
$$
\begin{align*}
\int x\,dx=\dfrac{1}{2}x^2+C
\end{align*}
$$
微分と積分の関係が、互いに逆の演算であることは次のように分かります。

$${\int x\,dx}$$ は、”インテグラル $${x}$$ ディー $${x}$$” と読みます。これは
”$${x}$$ の不定積分は $${\dfrac{1}{2}x^2+C}$$ であること”
つまり
”$${x}$$ を積分すると $${\dfrac{1}{2}x^2+C}$$ になること”
を意味します。
また、先の問題 (3), (4), (5) の結果
$$
\begin{align*}
\left(\dfrac{1}{2}x^2+C\right)'&=x より「x の不定積分は \dfrac{1}{2}x^2+C」\\
\left(\dfrac{1}{3}x^3+C\right)'&=x^2 より「x^2 の不定積分は \dfrac{1}{3}x^3+C」\\
\left(\dfrac{1}{4}x^4+C\right)'&=x^3 より「x^3 の不定積分は \dfrac{1}{4}x^4+C」
\end{align*}
$$
であることから
$$
\begin{align*}
\int x\,dx&=\dfrac{1}{2}x^2+C\\
\int x^2dx&=\dfrac{1}{3}x^3+C\\
\int x^3dx&=\dfrac{1}{4}x^4+C\\
\end{align*}
$$
これを一般化して、次の公式が成り立ちます。
<積分公式1>
$${n}$$ が $${0}$$ 以上の整数のとき
$$
\begin{align*}
\int x^ndx=\dfrac{1}{n+1}x^{n+1}+C(C は積分定数)
\end{align*}
$$
とくに $${n=0}$$ のときは、実数 $${x}$$ に対して
$${x^0=1}$$
と定義することによって
$${\int x^0dx=\int 1dx}$$
となりますが、このときは $${1}$$ を省略して
$${\int dx}$$
と書きます。
また、$${C}$$ は実数の値を取る定数で積分定数といいます。
不定積分という名前の由来は、積分定数 $${C}$$ の値が定まらないこと(不定であること)に由来します。
なお、今後「$${C}$$ は積分定数」と書くことを省略することがあります。
この公式をそのまま適用することによって
$$
\begin{align*}
\int dx&=\int x^0dx=\dfrac{1}{0+1}x^{0+1}+C=x+C\\[10pt]
\int x\,dx&=\int x^1dx=\dfrac{1}{1+1}x^{1+1}+C=\dfrac{1}{2}x^{2}+C\\[10pt]
\int x^2dx&=\dfrac{1}{2+1}x^{2+1}+C=\dfrac{1}{3}x^{3}+C\\[10pt]
\int x^3dx&=\dfrac{1}{3+1}x^{3+1}+C=\dfrac{1}{4}x^{4}+C\\[10pt]
\int x^4dx&=\dfrac{1}{4+1}x^{4+1}+C=\dfrac{1}{5}x^{5}+C\\
&\hspace{6pt}\vdots\\
\int x^{10}dx&=\dfrac{1}{10+1}x^{10+1}+C=\dfrac{1}{11}x^{11}+C\\
&\hspace{6pt}\vdots
\end{align*}
$$
以下同様と、形式的に積分できます。
さらに、関数の定数倍や,、そのたし算ひき算で表される関数の不定積分については、次の公式が成り立ちます。
<積分公式2>
$${k, l}$$ は $${0}$$ でない定数(実数)とすると
$$
\begin{align*}
&1. \int kf(x)dx=k\int f(x)dx\\
&2. \int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx\\
&3. \int \{f(x)-g(x)\}dx=\int f(x)dx-\int g(x)dx\\
&4. \int \{kf(x)+lg(x)\}dx=k\int f(x)dx+l\int g(x)dx\\
\end{align*}
$$
1. 2. 3. を一般化したのが 4. です。
これらの公式を用いた不定積分の具体例を上げます。
不定積分の具体例
(例1)$${2x^3}$$ の不定積分を求めなさい($${2x^3}$$ を積分しなさい)。
$$
\begin{align*}
\int 2x^3dx&=2\int x^3dx\\
&=\cancel{2}\cdot\dfrac{1}{\underset{2}{\cancel{4}}}x^4+C\\
&=\dfrac{1}{2}x^4+C
\end{align*}
$$
定数 $${2}$$ は積分の外にだして、$${x^3}$$ 部分を積分します。
(例2)$${4x^3-2x^2+5}$$ の不定積分を求めなさい($${4x^3-2x^2+5}$$ を積分しなさい)。
$$
\begin{align*}
\int (4x^3-2x^2+5)dx&=\int 4x^3dx-\int 2x^2dx+\int5dx\\
&=4\int x^3dx-2\int x^2dx+5\int dx\\
&=\cancel{4}\cdot\dfrac{1}{\cancel{4}}x^4-2\cdot\dfrac{1}{3}x^3+5\cdot x+C\\
&=x^4-\dfrac{2}{3}x^3+5x+C\\
\end{align*}
$$
関数のたし算ひき算で表される場合は、それぞれを別々に積分します。
なお、高校3年で習う数学Ⅲの微分積分では、指数 $${n}$$ は実数まで拡張されます(参考1で数の拡張)。
応用として、(参考2)<積分公式3>の方で簡単に解説します。
定積分
ここから定積分に入ります。まずは定積分の計算方法を示し、その定積分が囲われた面積になることを解説していきます。
関数 $${f(x)}$$ の不定積分の1つを $${F(x)}$$ とします。つまり
$$
\begin{align*}
\int f(x)dx=F(x)
\end{align*}
$$
不定積分の「1つ」とは、不定積分には積分定数 $${C}$$ の実数値を変えたものが無数にあるので、その中の「1つ」を任意に選ぶためです。
例えば $${x}$$ の不定積分は
$$
\begin{align*}
\int x\,dx=\dfrac{1}{2}x^2+C
\end{align*}
$$
ですが、積分定数 $${C}$$ は実数なので、その実数の違いだけ無数にあります。つまり、$${C}$$ の実数値を任意に1つ選んでもよいということです。
関数 $${f(x)}$$ の不定積分の1つを $${F(x)}$$ としたとき、2つの実数 $${a}$$, $${b}$$ について
$$
\begin{align*}
F(b)-F(a)
\end{align*}
$$
を、$${f(x)}$$ の $${a}$$ から $${b}$$ までの定積分といい、記号
$$
\begin{align*}
\int_{a}^{b} f(x) dx
\end{align*}
$$
で表します。つまり
$$
\begin{align*}
\int_{a}^{b} f(x) dx=F(b)-F(a)
\end{align*}
$$
定積分 $${\int_{a}^{b} f(x)dx}$$ の値を求めることを、関数 $${f(x)}$$ を $${a}$$ から $${b}$$ まで積分するといい、$${a}$$ をこの定積分の下端、$${b}$$ を上端といいます。
さらに
$$
\begin{align*}
F(b)-F(a)=\Big[F(x)\Big]_{a}^{b}
\end{align*}
$$
と、”四角カッコ” で不定積分 $${F(x)}$$ を明示することによって、定積分は次のステップで計算できます。
$$
\begin{align*}
\int_{a}^{b} f(x) dx=\Big[F(x)\Big]_{a}^{b}=F(b)-F(a)
\end{align*}
$$
***
つまり定積分は、一度不定積分 $${F(x)}$$ を求めてから、それに上端 $${b}$$ を代入した値から、下端 $${a}$$ を代入した値を引いて計算します。

これだけだと抽象的なので、具体例を上げます。
定積分の具体例
(例1)関数 $${x}$$ を $${1}$$ から $${5}$$ まで定積分する。
$${x}$$ の不定積分は
$${\int x\,dx=\dfrac{1}{2}x^2+C}$$
なので
$$
\begin{align*}
\int_{1}^{5} x\,dx&=\Big[\underset{x の不定積分}{\dfrac{1}{2}x^2+C}\Big]_{1}^{5}\\
&=\underset{上端 x=5 を代入}{\left(\dfrac{1}{2}\cdot5^2+C\right)}-\underset{下端 x=1 を代入}{\left(\dfrac{1}{2}\cdot1^2+C\right)}\\
&=\left(\dfrac{25}{2}+C\right)-\left(\dfrac{1}{2}+C\right)\\
&=\dfrac{25}{2}+C-\dfrac{1}{2}-C\\
&=\dfrac{25}{2}-\dfrac{1}{2}+\cancel{C}-\cancel{C}\\
&=\dfrac{\overset{12}{\cancel{24}}}{\underset{1}{\cancel{2}}}\\
&=12
\end{align*}
$$
(例2)関数 $${x^2}$$ を $${1}$$ から $${3}$$ まで定積分する。
$${x^2}$$ の不定積分は
$${\int x^2dx=\dfrac{1}{3}x^3+C}$$
なので
$$
\begin{align*}
\int_{1}^{3} x^2dx&=\Big[\underset{x^2 の不定積分}{\dfrac{1}{3}x^3+C}\Big]_{1}^{3}\\
&=\underset{上端 x=3 を代入}{\left(\dfrac{1}{3}\cdot3^3+C\right)}-\underset{下端 x=1 を代入}{\left(\dfrac{1}{3}\cdot1^3+C\right)}\\
&=\left(\dfrac{27}{3}+C\right)-\left(\dfrac{1}{3}+C\right)\\
&=\dfrac{27}{3}+C-\dfrac{1}{3}-C\\
&=\dfrac{27}{3}-\dfrac{1}{3}+\cancel{C}-\cancel{C}\\
&=\dfrac{26}{3}
\end{align*}
$$
なお、上で計算したように、定積分を計算するにあたって積分定数 $${C}$$ は $${C-C=0}$$ で消えます。つまり、定積分の値は積分定数 $${C}$$ の値に無関係に定まるので、定積分の計算は次の(例)のように、積分定数 $${C}$$ を省いて行うのが普通です。
(例3)関数 $${x^2+x+1}$$ を $${-1}$$ から $${2}$$ まで定積分する。
$${x^2+x+1}$$ の不定積分は
$${\int (x^2+x+1)dx=\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+x+C}$$
なので
$$
\begin{align*}
\int_{-1}^{2} (x^2+x+1)dx&=\Big[\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+x\Big]_{-1}^{2} (\leftarrow C を省く)\\
&=\left(\dfrac{1}{3}\cdot2^3+\dfrac{1}{2}\cdot2^2+2\right)-\left(\dfrac{1}{3}\cdot{(-1)}^3+\dfrac{1}{2}\cdot{(-1)}^2+(-1)\right)\\
&=\left(\dfrac{8}{3}+\dfrac{4}{2}+2\right)-\left(-\dfrac{1}{3}+\dfrac{1}{2}-1\right)\\
&=\dfrac{8}{3}+\dfrac{4}{2}+2+\dfrac{1}{3}-\dfrac{1}{2}+1\\
&=\dfrac{8}{3}+\dfrac{1}{3}+\dfrac{4}{2}-\dfrac{1}{2}+2+1\\
&=\dfrac{\overset{3}{\cancel{9}}}{\cancel{3}}+\dfrac{3}{2}+3\\
&=3+\dfrac{3}{2}+3\\
&=6+\dfrac{3}{2}\\
&=\dfrac{12}{2}+\dfrac{3}{2}\\
&=\dfrac{15}{2}
\end{align*}
$$
(例4)関数 $${2x^3+4x}$$ を $${0}$$ から $${3}$$ まで定積分する。
$${2x^3+4x}$$ の不定積分は
$$
\begin{align*}
\int(2x^3+4x)dx&=\cancel{2}\cdot\dfrac{1}{\underset{2}{\cancel{4}}}x^4+\overset{2}{\cancel{4}}\cdot\dfrac{1}{\cancel{2}}x^2+C\\
&=\dfrac{1}{2}x^4+2x^2+C\\
\end{align*}
$$
なので
$$
\begin{align*}
\int_{0}^{3} (2x^3+4x)dx&=\Big[\dfrac{1}{2}x^4+2x^2\Big]_{0}^{3} (\leftarrow C を省く)\\
&=\left(\dfrac{1}{2}\cdot3^4+2\cdot3^2\right)-\left(\dfrac{1}{2}\cdot0^4+2\cdot0^2\right)\\
&=\dfrac{1}{2}\cdot81+2\cdot9-0\\
&=\dfrac{81}{2}+18\\
&=\dfrac{81}{2}+\dfrac{36}{2}\\
&=\dfrac{117}{2}
\end{align*}
$$
定積分が面積になること
定積分の重要な性質として、次の性質があります。
<定積分は囲われた面積>
区間 $${a\leqq x \leqq b}$$ で $${f(x)\geqq0}$$ の場合を考えます。つまり、下図のように $${y=f(x)}$$ のグラフが、$${a\leqq x \leqq b}$$ の範囲で $${x}$$ 軸より上側(接する場合も含む)にある場合です。

このとき、$${\int_{a}^{b} f(x) dx}$$ の値は、曲線 $${y=f(x)}$$ と $${x}$$ 軸、および2直線 $${x=a}$$ と $${x=b}$$ で囲まれた部分の面積を表します。下図の黒塗部分の面積です。

***
定積分が面積になることの証明は、高校の微分積分で習います(証明は割愛します)。
簡単な例題を通して、定積分が面積になることを確認します。
(例題1)
下図のように、直線 $${y=3}$$ と $${x=4}$$、および $${x}$$ 軸と $${y}$$ 軸とで囲まれた部分の面積を、定積分を用いて求めなさい。

なお、直線 $${y=3}$$ とは $${x}$$ 軸に平行な直線($${x}$$ の値に関係なく $${y}$$ 座標が常に $${3}$$ になる直線)、直線 $${x=4}$$ とは $${y}$$ 軸に平行な直線($${y}$$ の値に関係なく $${x}$$ 座標が常に $${4}$$ になる直線)です。
(解答)
関数 $${y=3}$$ を $${0}$$ から $${4}$$ まで定積分すればいいので
$$
\begin{align*}
\int_{0}^{4} 3dx&=3\int_{0}^{4} dx\\
&=3\Big[x\Big]_{0}^{4}\\
&=3(4-0)\\
&=3\cdot4\\
&=12
\end{align*}
$$
これは、下図のように縦 $${3}$$、横 $${4}$$ の長方形の面積
縦$${\times}$$横 $${=3\times4=12}$$
と同じになります。確かに積分の値は面積になります。

(例題2)
下図のように、直線 $${y=2x}$$ と $${x=2}$$ 、および $${x}$$ 軸とで囲まれた部分の面積を、定積分を用いて求めなさい。
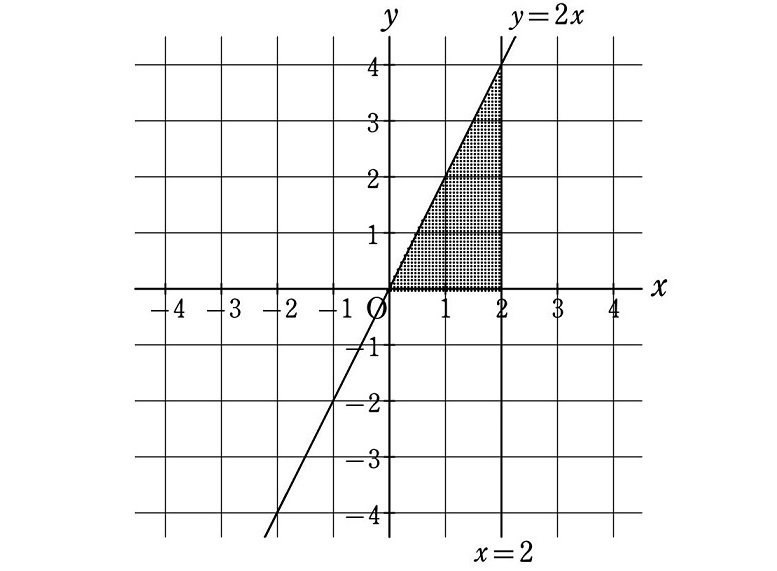
(解答)
関数 $${y=2x}$$ を $${0}$$ から $${2}$$ まで定積分すればいいので
$$
\begin{align*}
\int_{0}^{2} 2xdx&=2\int_{0}^{2} xdx\\
&=2\Big[\dfrac{1}{2}x^2\Big]_{0}^{2}\\
&=2(\dfrac{1}{2}\cdot2^2-\dfrac{1}{2}\cdot0^2)\\
&=2(\dfrac{1}{2}\cdot4-0)\\
&=\cancel{2}\cdot\dfrac{1}{\cancel{2}}\cdot4\\
&=4
\end{align*}
$$
これは、下図のように底辺 $${2}$$、高さ $${4}$$ の直角三角形の面積
底辺$${\times}$$高さ$${\times \dfrac{1}{2}=\cancel{2}\times4\times\dfrac{1}{\cancel{2}}=4}$$
と同じになります。確かに積分の値は面積になります。

(例題3)
下図のように、曲線 $${y=x^2}$$ と直線 $${x=-2}$$、$${x=1}$$、および $${x}$$ 軸とで囲まれた部分の面積を、定積分を用いて求めなさい。

(解答)
関数 $${y=x^2}$$ を $${-2}$$ から $${1}$$ まで定積分すればいいので
$$
\begin{align*}
\int_{-2}^{1} x^2dx&=\Big[\dfrac{1}{3}x^3\Big]_{-2}^{1}\\
&=\dfrac{1}{3}\cdot1^3-\dfrac{1}{3}\cdot{(-2)}^3\\
&=\dfrac{1}{3}\cdot1-\dfrac{1}{3}\cdot(-8)\\
&=\dfrac{1}{3}+\dfrac{8}{3}\\
&=\dfrac{\overset{3}{\cancel{9}}}{\cancel{3}}\\
&=3
\end{align*}
$$
グラフは原点 O で $${x}$$ 軸と接していますが、そのまま定積分してもかまいません。
いろいろな関数の積分
ここでは、いろいろな関数の積分を紹介します。これらは公式として用いられます。積分は微分の逆演算なので、微分の公式をもとにして定積分の公式を得ることができます。
ここでは結果だけを列挙します(高校の数学Ⅲの微分積分で習います)。
<三角関数の不定積分>
$${\int \sin x\,dx=-\cos x+C}$$
$${\int \cos x\,dx=\sin x+C}$$
$${\int \dfrac{1}{\cos^2x}dx=\tan x+C}$$
<指数関数の不定積分>
$${\int a^x dx=\dfrac{a^x}{\log a}+C}$$($${a}$$ は $${1}$$ でない正の定数)
$${\int e^xdx=e^x+C}$$
なお、$${\log x}$$ は $${e}$$ を底とする対数で
$${\log_e x=\log x}$$
と $${e}$$ を省略して書くのが普通です。この $${e}$$ は $${e=2.71828 \cdots}$$ となる無理数の定数で、ネイピア数(Napier's constant)とよばれています。
この $${e}$$ を低とする対数 $${\log x}$$ を、$${x}$$ の自然対数といいます。
また、$${10}$$ を低とする対数 $${\log_{10} x}$$ を、$${x}$$ の常用対数といいます。
最後の $${e^x}$$ は(積分定数は付きますが)積分しても変化しない関数です。微分しても変化しないことと同様に、積分しても変化しません。
数学、物理、工学など、勉強が進めばこの $${e^x}$$ が重要な役割を演じることになるので
$$
\begin{align*}
(e^x)'&=e^x(微分しても変わらない)\\
\int e^xdx&=e^x+C(積分しても変わらない)
\end{align*}
$$
は特に押さえておきましょう。
$$
\begin{align*}
\\[-14pt]
&\hspace{30pt}\xrightarrow[]{ 微分する}\\[-12.5pt]
&e^x+C\hspace{46pt}e^x\\[-12.5pt]
&\hspace{30pt}\xleftarrow[ 積分する]{}
\end{align*}
$$
(参考1)数の分類
数の分類は以下の通りです。
$$
\begin{align*}
\boldsymbol{複素数 a+bi}
\begin{cases}
\overset{\small b=0 のとき}{\boldsymbol{実数 a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数} \scriptsize{(1, 2, 3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数} \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
{\footnotesize 例 0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize(循環する無限小数)}}\\
{\footnotesize 例 0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
{\scriptsize 例 \pi (=3.1415\cdots) のような \boldsymbol{循環しない無限小数}}\\
{\scriptsize e (=2.7182\cdots) のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0 のとき}{\boldsymbol{虚数 a+bi}} 特に a=0 のとき \boldsymbol{bi} を\boldsymbol{純虚数}という。
\end{cases}
\end{align*}
$$
(参考2)<積分公式3>
$${x^n}$$($${n}$$ は $${0}$$ 以上の整数)の不定積分ついて、以下のように $${n}$$ の範囲は実数まで拡張されます(高校の数学Ⅲの微分積分で習います)。
<積分公式3>
$${\int x^\alpha dx}$$($${\alpha}$$ は実数)について
(case1) $${\alpha}$$ が $${-1}$$ 以外の実数のとき
$$
\begin{align*}
\int x^\alpha dx=\dfrac{1}{\alpha+1}x^{\alpha+1}+C (\alpha\ne-1)
\end{align*}
$$
(case2) $${\alpha=-1}$$ のとき
$$
\begin{align*}
\int x^{-1} dx=\int \dfrac{1}{x}\,dx=\log|x|+C\\
\end{align*}
$$
***
$${\alpha=-1}$$ のときは $${\dfrac{1}{\alpha+1}}$$ の分母が $${0}$$ になり、(case2) として別扱いになります。これは $${\log|x|}$$ の微分
$${(\log|x|)'=\dfrac{1}{x}}$$
の逆演算として証明されます。これも
$${(\log x)'=\dfrac{1}{x}}$$
と合わせて微分公式として覚えておきましょう。
(追記)絶対値について
なお、$${|x|}$$ を $${x}$$ の絶対値といい、$${| |}$$ を絶対値記号といいます。絶対値は次のように計算します。
$$
\begin{align*}
&x\geqq0 のとき |x|=x\\
&x<0 のとき |x|=-x
\end{align*}
$$
***
絶対値 $${| |}$$ の中身が $${0}$$ 以上のときはそのまま絶対値をはずし、中身が負のときはマイナスをかけて絶対値をはずします。つまり、結果がマイナスの値にならないようにします。
$$
\begin{align*}
&\left|2\right|=2 & &\small{(そのまま絶対値をはずす)}\\
&\left|\sqrt{5}\right|=\sqrt{5} & &\small{(そのまま絶対値をはずす)}\\
&\left|-2\right|=-(-2)=2 & &\small{(マイナスをかけて絶対値をはずす)}\\
&\left|-\sqrt{5}\right|=-(-\sqrt{5})=\sqrt{5} & &\small{(マイナスをかけて絶対値をはずす)}\\
&\left|0\right|=0 & &\small{(0 のときはそのまま絶対値をはずす)}
\end{align*}
$$
実数の絶対値は、数直線における原点 O からの距離とみなすことができます。例えば
原点 O から $${2}$$ までの距離は $${|2|=2}$$
原点 O から $${-2}$$ までの距離は $${|-2|=2}$$
原点 O から $${-5}$$ までの距離は $${|-5|=5}$$

<積分公式3>を用いた具体例をあげます。
(例1)
$$
\begin{align*}
\int x^{\sqrt{2}}dx&=\dfrac{1}{\sqrt{2}+1}x^{\sqrt{2}+1}+C\\[10pt]
\int x^{-\sqrt{5}}dx&==\dfrac{1}{-\sqrt{5}+1}x^{-\sqrt{5}+1}+C
\end{align*}
$$
(例2) 指数が負の整数のときは
$${x^{-1}=\dfrac{1}{x}\raisebox{3ex}{ }}$$
$${x^{-2}=\dfrac{1}{x^2}\raisebox{3ex}{ }}$$
$${x^{-3}=\dfrac{1}{x^3}\raisebox{3ex}{ }}$$
$${\hspace{32pt}\vdots}$$
以下同様、と定義されることにより(高校2年で習う指数の拡張)、$${\alpha}$$ が $${-1}$$ 以外の負の整数($${-2, -3, -4, \cdots}$$)のときは
$$
\begin{align*}
\int\dfrac{1}{x^2}\,dx&=\int x^{-2}dx\\
&=\dfrac{1}{-2+1}x^{-2+1}+C\\
&=\dfrac{1}{-1}x^{-1}+C\\
&=-x^{-1}+C\\
&=-\dfrac{1}{x}+C
\end{align*}
$$
$$
\begin{align*}
\int\dfrac{1}{x^3}\,dx&=\int x^{-3}dx\\
&=\dfrac{1}{-3+1}x^{-3+1}+C\\
&=\dfrac{1}{-2}x^{-2}+C\\
&=-\dfrac{1}{2}\cdot\dfrac{1}{x^2}+C\\
&=-\dfrac{1}{2x^2}+C
\end{align*}
$$
$$
\begin{align*}
\int\dfrac{1}{x^4}\,dx&=\int x^{-4}dx\\
&=\dfrac{1}{-4+1}x^{-4+1}+C\\
&=\dfrac{1}{-3}x^{-3}+C\\
&=-\dfrac{1}{3}\cdot\dfrac{1}{x^3}+C\\
&=-\dfrac{1}{3x^3}+C
\end{align*}
$$
以下同様と計算されます。
なお、(case2) の $${\dfrac{1}{x}}$$ の不定積分は、よく出るので公式として覚えておきましょう。改めて掲載しておきます。
$$
\begin{align*}
\int \dfrac{1}{x}\,dx=\log|x|+C\\
\end{align*}
$$
$${\log|x|}$$ と $${x}$$ に絶対値がついているので、$${x}$$ の範囲は $${0}$$ 以外のすべての実数で定義されています。それは、$${\log|x|}$$ の真数部分 $${|x|}$$ は $${0}$$ より大きい($${|x|>0}$$)という真数条件を満たすためです。$${x>0}$$ でも $${x<0}$$ でも、真数条件 $${|x|>0}$$ は満たします。
(追記)真数条件
対数 $${\log_aM}$$ について、真数 $${M}$$ は $${M>0}$$ を満たさなければならない。
***
真数条件は高校の指数対数で詳しく習います。
なお、$${x=0}$$ のときは、$${\dfrac{1}{x}}$$ の分母が $${0}$$ になり、かつ
$${|x|=|0|=0}$$
と真数条件も満たさなくなるので定義されていません。
