
中学でも分かる➄「対数関数」
前回は指数関数を勉強しました。今回はその指数関数と関連のある対数関数を勉強します。
まずは対数の基本を勉強し、そのあと対数関数、そして常用対数と勉強を進めていきます。なお、この記事を読むにあたって
中学でも分かる➂「平方根」
中学でも分かる④「指数関数」
での知識が登場しますので、苦手な場合は折にふれ戻るか、あらかじめ読んでおくと読みやすくなります。
まずは、前回やった指数関数の復習です。
指数関数の定義とグラフ(復習)
$${0< a<1}$$ または $${1< a}$$ のとき、関数 $${y=a^x}$$ を、$${a}$$ を底とする $${x}$$ の指数関数という。指数関数のグラフは次のようになる。
(case1) $${0< a <1}$$ のとき
(case2) $${1< a}$$ のとき
で場合分けをする。

***
対数について
$${y=2^x}$$ のグラフは、$${x}$$ の値が増加すると $${y}$$ の値も増加します。よって、$${2^r=3}$$ を満たす $${r}$$ はただ1つ存在し、それを
$$
\begin{align*}
r=\log_2 3
\end{align*}
$$
と表します。これを、$${2}$$ を底とする $${3}$$ の対数といい、"ログ $${2}$$ 底の $${3}$$" または "ログ $${2}$$ の $${3}$$" と読みます。
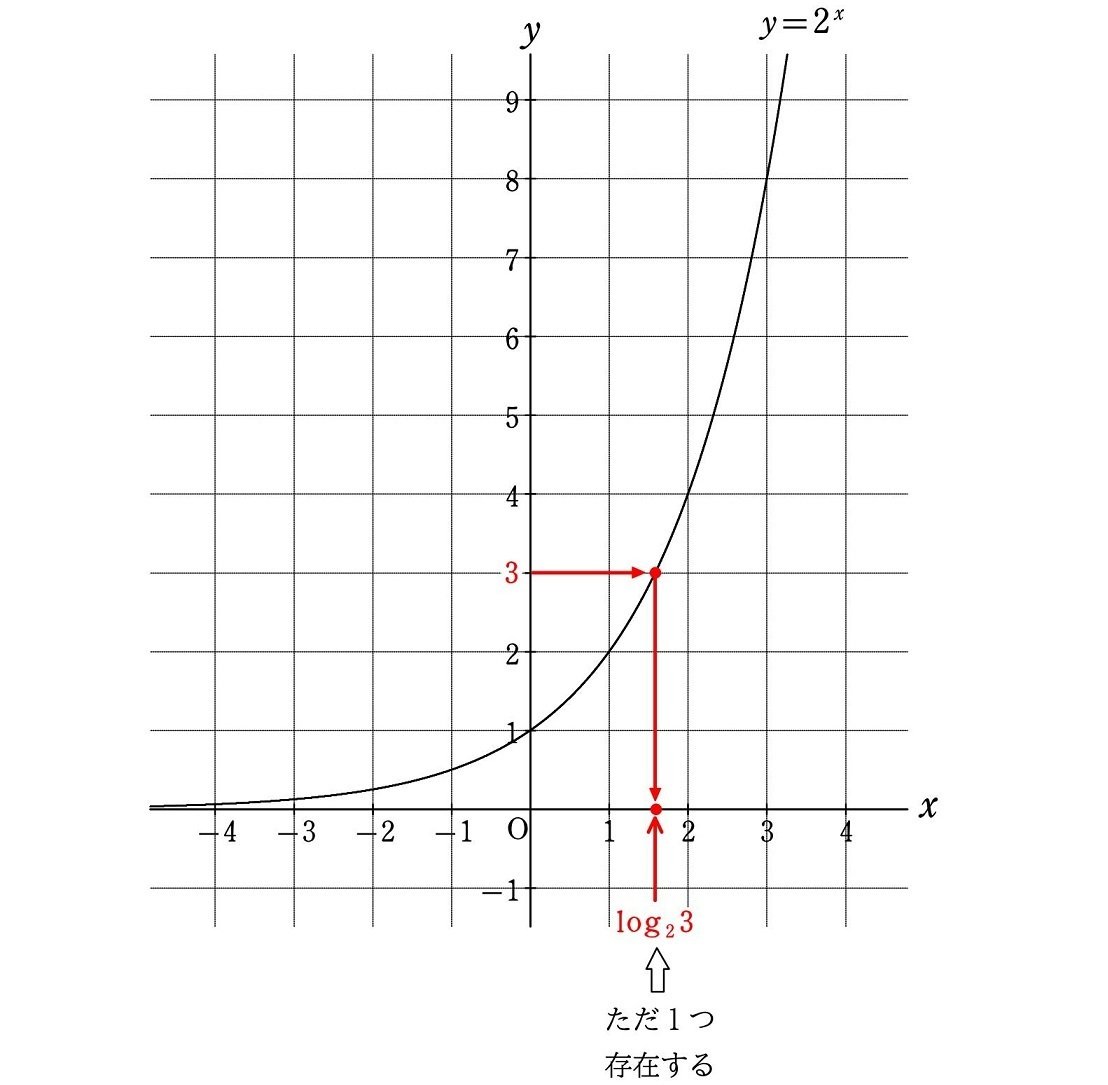
一般の指数関数
$$
\begin{align*}
y=a^x
\end{align*}
$$
について、上と同様に考えることによって対数の定義を与えることができます。
<対数の定義>
$${a}$$ について、$${0< a<1}$$ または $${1< a}$$(底の条件)
$${R}$$ について、$${R>0}$$(真数条件)
のとき、任意の正の実数 $${R}$$ に対して、$${a^r=R}$$ となる $${r}$$ の値がただ1つ決まる。この $${r}$$ を、$${a}$$ を底とする $${R}$$ の対数といい、 $${r=\log_a R}$$ と表す。つまり
$$
\begin{align*}
R=a^r \Longleftrightarrow r=\log_a R
\end{align*}
$$
***
なお、対数 $${\log_a R}$$ を考えるにあたっては、底の条件と真数条件をおさえておきましょう。
底 $${a}$$ は、$${0< a<1}$$ または $${1< a}$$ を満たす任意の実数です(底の条件)。
真数は、$${R>0}$$ を満たす任意の実数です(真数条件)。
これは、もともとの指数関数 $${a^r=R}$$ を考えるにあたって必ず満たしている条件で、対数に変換してもその条件は継続されます。
対数を考えるときは、この条件が必ず付きます。明示しない場合もあるので、この条件はつねに確認するようにしましょう。
いくつか例を与えます。
$${a^r=R}$$ より $${r=\log_a R}$$
に当てはめて
$${2^4=16}$$ より $${4=\log_2 16}$$
$${2^3=8}$$ より $${3=\log_2 8}$$
$${2^2=4}$$ より $${2=\log_2 4}$$
$${2^1=2}$$ より $${1=\log_2 2}$$
$${2^0=1}$$ より $${0=\log_2 1}$$
$${2^{-1}=\dfrac{1}{2}}$$ より $${-1=\log_2 \dfrac{1}{2}\raisebox{2ex}{ }}$$
$${2^{-2}=\dfrac{1}{4}}$$ より $${-2=\log_2 \dfrac{1}{4}\raisebox{3ex}{ }}$$
$${3^2=9}$$ より $${2=\log_3 9}$$
$${5^{-1}=\dfrac{1}{5}}$$ より $${-1=\log_5\dfrac{1}{5}\raisebox{3ex}{ }}$$
$${\left(\dfrac{1}{2}\right)^3=\dfrac{1}{8}}$$ より $${3=\log_{\frac{1}{2}} \dfrac{1}{8}\raisebox{3ex}{ }}$$
(対数のポイント1)
累乗と対数の変換では、「底は底」というキーワードで覚えればよいでしょう。
底 $${a}$$ の位置を固定して覚えて、”$${R=}$$” と ”$${r=}$$” が入れ替わります。

(例)
$$
\begin{align*}
&8=\hspace{0pt}\underset{底}{2}^3 \Longleftrightarrow 3=\log_{\underset{底}{2}}\hspace{-1pt}8\\
&\dfrac{1}{9}=\hspace{0pt}\underset{底}{3}^{-2} \Longleftrightarrow -2=\log_{\underset{底}{3}}\hspace{0pt}\dfrac{1}{9}
\end{align*}
$$
(対数のポイント2)
$${\log_a R}$$ は、
「$${a}$$ を何乗すると $${R}$$ になりますか?」
を聞いています。つまり $${a^r=R}$$ より
「$${a}$$ を $${\underline{r}}$$ 乗すると $${R}$$ になる」
ので
$$
\begin{align*}
\log_a R=\underline{r}
\end{align*}
$$
となります。先ほどの例でいうと
$${2}$$ は $${\underline{4}}$$ 乗すると $${16}$$ なので $${\log_2 16=\underline{4}}$$
$${2}$$ は $${\underline{3}}$$ 乗すると $${8}$$ なので $${\log_2 8=\underline{3}}$$
$${2}$$ は $${\underline{2}}$$ 乗すると $${4}$$ なので $${\log_2 4=\underline{2}}$$
$${2}$$ は $${\underline{1}}$$ 乗すると $${2}$$ なので $${\log_2 2=\underline{1}}$$
$${2}$$ は $${\underline{0}}$$ 乗すると $${1}$$ なので $${\log_2 1=\underline{0}}$$
$${2}$$ は $${\underline{-1}}$$ 乗すると $${\dfrac{1}{2}}$$ なので $${\log_2 \dfrac{1}{2}=\underline{-1}\raisebox{3ex}{ }}$$
$${2}$$ は $${\underline{-2}}$$ 乗すると $${\dfrac{1}{4}}$$ なので $${\log_2 \dfrac{1}{4}=\underline{-2}\raisebox{3ex}{ }}$$
$${3}$$ は $${\underline{2}}$$ 乗すると $${9}$$ なので $${\log_3 9=\underline{2}}$$
$${5}$$ は $${\underline{-1}}$$ 乗すると $${\dfrac{1}{5}}$$ なので $${\log_5 \dfrac{1}{5}=\underline{-1}\raisebox{3ex}{ }}$$
$${\dfrac{1}{2}}$$ は $${\underline{3}}$$ 乗すると $${\dfrac{1}{8}}$$ なので $${\log_{\frac{1}{2}} \dfrac{1}{8}=\underline{3}\raisebox{3ex}{ }}$$
ここから、対数の重要な性質をいくつか述べていきます。
もっとも基本的な性質として、次のものがあります。
<対数の重要性質1>
$${0< a<1}$$ または $${1< a}$$ のとき
1. $${\log_a 1=0}$$(真数が $${1}$$ のときは、つねに $${0}$$)
2. $${\log_a a=1}$$(真数が底と同じときは、つねに $${1}$$)
***
(証明)
累乗 $${a^r}$$ において、$${r}$$ を $${0, 1}$$ とすると、それぞれ
$$
\begin{align*}
&a^0=1 \Longleftrightarrow \log_a 1=0\\
&a^1=a \Longleftrightarrow \log_a a=1
\end{align*}
$$
(証明終)
要するに
1.$${a}$$ は $${\underline{0}}$$ 乗すると $${1}$$ なので $${\log_a 1=\underline{0}}$$
2.$${a}$$ は $${\underline{1}}$$ 乗すると $${a}$$ なので $${\log_a a=\underline{1}}$$
この性質は頻繁に出てくるので、覚えておくようにしましょう。
(例)
真数が $${1}$$ のときは、つねに $${0}$$ です。
$${\log_2 1=0}$$
$${\log_3 1=0}$$
$${\log_{\frac{1}{2}} 1=0}$$
真数が底と同じときは、つねに $${1}$$ です。
$${\log_2 2=1}$$
$${\log_3 3=1}$$
$${\log_{\frac{1}{2}} \frac{1}{2}=1}$$
さて、累乗については、次の指数法則が成り立ちました。
<指数法則>
$${a>0, b>0}$$ で、$${x, y}$$ が実数のとき
$$
\begin{align*}
1. a^xa^y=a^{x+y} 2. (a^x)^y=a^{xy} 3. {(ab)}^x=a^xb^x
\end{align*}
$$
***
この指数法則と対数の定義から、次の性質が導かれます。
<対数の重要性質2>
$${a}$$ については、$${0< a<1}$$ または $${1< a}$$(底の条件)
$${M}$$ については、$${M>0}$$(指数条件)
$${N}$$ については、$${N>0}$$(指数条件)
で、$${p}$$ が実数のとき
1. $${\log_a MN=\log_a M+\log_a N}$$
2. $${\log_a \dfrac{M}{N}=\log_a M-\log_a N}$$
3. $${\log_a M^p=p\log_a M}$$
特に、$${M=a}$$ のときは
4. $${\log_a a^p=p\log_a a=p}$$
***
これらを証明しましょう。$${x, y}$$ を実数とします。
(1. の証明)
指数法則 $${a^xa^y=a^{x+y}}$$ について
$${a^x=M {\small \cdots (*1)}}$$
$${a^y=N {\small \cdots (*2)}}$$
とおくと
$${MN=a^{x+y} {\small \cdots (*3)}}$$
対数の定義より
$${\small{(*1)} \Leftrightarrow x=\log_a M {\small \cdots (*4)}}$$
$${\small{(*2)} \Leftrightarrow y=\log_a N {\small \cdots (*5)}}$$
$${\small{(*3)} \Leftrightarrow x+y=\log_a MN {\small \cdots (*6)}}$$
$${\small{(*4)}, \small{(*5)}}$$ を$${\small{(*6)}}$$ に代入して
$${\log_a M+\log_a N=\log_a MN}$$
よって
$${\log_a MN=\log_a M+\log_a N}$$
(2. の証明)
指数法則 $${a^xa^y=a^{x+y}}$$ について、$${y}$$ は実数より $${-y}$$ も実数となる。よって、$${y}$$ を $${-y}$$ に置き換えてもよいので
$${a^xa^{-y}=a^{x+(-y)}}$$
$${a^xa^{-y}=a^{x-y}}$$
累乗の定義より $${a^{-y}=\dfrac{1}{a^y}}$$ なので(中学でも分かる④「指数関数」参照)
$${a^x\cdot\dfrac{1}{a^y}=a^{x-y}}$$
$${\dfrac{a^x}{a^y}=a^{x-y}}$$
ここで
$${a^x=M {\small \cdots (*1)}}$$
$${a^y=N {\small \cdots (*2)}}$$
とおくと
$${\dfrac{M}{N}=a^{x-y} {\small \cdots (*7)}}$$
対数の定義より
$${\small{(*1)} \Leftrightarrow x=\log_a M {\small \cdots (*4)}}$$
$${\small{(*2)} \Leftrightarrow y=\log_a N {\small \cdots (*5)}}$$
$${\small{(*7)} \Leftrightarrow x-y=\log_a \dfrac{M}{N} {\small \cdots (*8)}}$$
$${\small{(*4)}, \small{(*5)}}$$ を$${\small{(*8)}}$$ に代入して
$${\log_a M-\log_a N=\log_a \dfrac{M}{N}}$$
よって
$${\log_a \dfrac{M}{N}=\log_a M-\log_a N}$$
(3. の証明)
指数法則 $${(a^x)^p=a^{xp}}$$ について
$${a^x=M {\small \cdots (*1)}}$$
とおくと
$${M^p=a^{xp} {\small \cdots (*9)}}$$
対数の定義より
$${\small{(*1)} \Leftrightarrow x=\log_a M {\small \cdots (*4)}}$$
$${{\small (*9)} \Leftrightarrow xp=\log_a M^p}$$
より
$${\log_a M^p=px}$$
これに $${(*4)}$$ を代入して
$${\log_a M^p=p\log_a M}$$
(4. の証明)
特に $${M=a}$$ のときは、すでに示した $${\log_a a=1}$$ を用いて
$${\log_a a^p=p\log_a a=p\cdot1=p}$$
(証明終)
この対数の性質を用いて、次のように計算できます。
なお、<対数の重要性質1>の 2.
$${\log_{a}a=1}$$
より
$${\log_{2}2=1}$$
$${\log_{3}3=1}$$
$${\log_{10}10=1}$$
となることを確認しましょう。底と真数が同じときの対数は、つねに $${1}$$ です。今後このような計算は当たり前のように出てくるので覚えておきましょう。
(例)
(1) $${\log_{10} 2+\log_{10} 5=\log_{10}(2\times5)=\log_{10} 10=1}$$
(2) $${\log_3 7-\log_3 63=\log_3 \dfrac{7}{63}=\log_3 \dfrac{1}{9}=\log_3 \dfrac{1}{3^2}=\log_3 3^{-2}=-2\underset{1}{\underline{\log_3 3}}=-2\cdot1=-2}$$
(3) $${\log_2 \sqrt[5]{2}=\log_2 2^{\frac{1}{5}}=\dfrac{1}{5}\underset{1}{\underline{\log_2 2}}=\dfrac{1}{5}\cdot1=\dfrac{1}{5}}$$
次の公式も重要です。
<底の変換公式>
$${a}$$ については、$${0< a<1}$$ または $${1< a}$$(底の条件)
$${b}$$ については、$${0< b<1}$$ または $${1< b}$$(底の条件)
$${u}$$ については、$${u>0}$$(真数条件)
のとき
$$
\begin{align*}
\log_a u=\dfrac{\log_b u}{\log_b a}
\end{align*}
$$
***
この公式により、底が $${a}$$ の対数を、底が $${b}$$ の対数に変換することができます。

(証明)
$${r=\log_a u}$$ とおくと、対数の定義より
$${u=a^r}$$
$${0< b<1}$$ または $${1< b}$$ として、$${b}$$ を底とする $${u}$$ の対数をとると
$${\log_b u=\log_b a^r}$$
<対数の重要性質2>の 3. より、指数部分は前に出せるので
$${\log_b u=r\log_b a}$$
$${r\log_b a=\log_b u {\small \cdots (*10)}}$$
ここで、$${a=1}$$ のときのみ
$${\log_b a=\log_b 1=0}$$
であり、それ以外 $${0< a<1}$$ または $${1< a}$$(底の条件)のもとでは、任意の実数 $${a}$$ に対して
$${\log_b a\ne0}$$
になるので、$${(10)}$$ の両辺を $${\log_b a (\ne0)}$$ で割って
$${r=\dfrac{\log_b u}{\log_b a}}$$
$${r=\log_a u}$$ とおいたので
$${\log_a u=\dfrac{\log_b u}{\log_b a}}$$
(証明終)
例えば、$${\log_8 16}$$ は、底の変換公式を用いて
$${\log_8 16=\hspace{-6pt}\underset{底を 2 に変換}{\dfrac{\log_2 16}{\log_2 8}}\hspace{-6pt}=\dfrac{\log_2 2^4}{\log_2 2^3}=\dfrac{4\log_2 2}{3\log_2 2}=\dfrac{4}{3}}$$
と計算できます。
問題 次の式を簡単にしなさい。
(1) $${\log_9 27}$$ (2) $${\log_3 4\cdot\log_4 9}$$
解説
(1) $${\log_9 27=\hspace{-6pt}\underset{底を 3 に変換}{\dfrac{\log_3 27}{\log_3 9}}\hspace{-6pt}=\dfrac{\log_3 3^3}{\log_3 3^2}=\dfrac{3\log_3 3}{2\log_3 3}=\dfrac{3}{2}}$$
(2) $${\log_3 4\cdot\log_4 9=\cancel{\log_3 4}\cdot\hspace{-7pt}\underset{底を 3 に変換}{\dfrac{\log_3 9}{\cancel{\log_3 4}}}\hspace{-6pt}=\log_3 3^2=2\log_3 3=2}$$
対数関数
底が $${2}$$ の関数 $${y=\log_2 x}$$ のグラフについて考えます。なお、この関数の定義域($${x}$$ の範囲)は、真数条件より正の実数 $${x>0}$$ です。
ここで、関数 $${y=\log_2 x}$$ のグラフを描いてみます。そのために、いくつかの $${x (>0)}$$ について $${y}$$ の値を計算しましょう。
$$
\begin{align*}
x=&8 のとき\\
&y=\log_2 8=\log_2 2^3=3\log_2 2=3\\
x=&4 のとき\\
&y=\log_2 4=\log_2 2^2=2\log_2 2=2\\
x=&2 のとき\\
&y=\log_2 2=1\\
x=&1 のとき\\
&y=\log_2 1=0\footnotesize{(底が 1 のときは 0)}\\
x=&\dfrac{1}{2} のとき\\
&y=\log_2 \dfrac{1}{2}=\log_2 2^{-1}=-\log_2 2=-1\\
x=&\dfrac{1}{4} のとき\\
&y=\log_2 \dfrac{1}{4}=\log_2 \dfrac{1}{2^2}=\log_2 2^{-2}=-2\log_2 2=-2\\
x=&\dfrac{1}{8} のとき\\
&y=\log_2 \dfrac{1}{8}=\log_2 \dfrac{1}{2^3}=\log_2 2^{-3}=-3\log_2 2=-3
\end{align*}
$$
以上の結果を表にすると、次のようになります。
$$
\def\arraystretch{1.7}
\begin{array}{c|c|c|c|c|c|c|c}
x & \dfrac{1}{8} & \dfrac{1}{4} & \dfrac{1}{2} & 1 & 2 & 4 & 8 \\ \hline
y & -3 & -2 & -1 & 0 & 1 & 2 & 3\\
\end{array}
$$
これらの値を $${(x, y)}$$ 座標
$${\mathrm{P}(8, 3)}$$
$${\mathrm{Q}(4, 2)}$$
$${\mathrm{R}(2, 1)}$$
$${\mathrm{S}\,(1, 0)}$$
$${\mathrm{T}\,(\,\dfrac{1}{2}, -1)\raisebox{2.5ex}{ }}$$
$${\mathrm{U}\,(\,\dfrac{1}{4}, -2)\raisebox{2.5ex}{ }}$$
$${\mathrm{W}(\,\dfrac{1}{8}, -3)\raisebox{2.5ex}{ }}$$
として、下図のように $${xy}$$ 座標に打ち込んでいきます。

$${x}$$ が無理数のときも加えていきましょう。新たに加えられたのが赤点です(ルート $${\sqrt{ }}$$ の計算は、中学でも分かる➃「指数関数」参照)。
$$
\begin{align*}
x=&\sqrt{32} のとき\\
&y=\log_2 \sqrt{32}=\log_2 \sqrt{2^5}=\log_2 2^{\frac{5}{2}}=\dfrac{5}{2}\log_2 2=\dfrac{5}{2}\\
x=&\sqrt{8} のとき\\
&y=\log_2 \sqrt{8}=\log_2 \sqrt{2^3}=\log_2 2^{\frac{3}{2}}=\dfrac{3}{2}\log_2 2=\dfrac{3}{2}\\
x=&\sqrt{2} のとき\\
&y=\log_2 \sqrt{2}=\log_2 2^{\frac{1}{2}}=\dfrac{1}{2}\log_2 2=\dfrac{1}{2}\\
x=&\frac{1}{\sqrt{2}} のとき\\
&y=\log_2 \frac{1}{\sqrt{2}}=\log_2 \frac{1}{2^{\frac{1}{2}}}=\log_2 2^{\tiny{-}\frac{1}{2}}=-\dfrac{1}{2}\log_2 2=-\dfrac{1}{2}\\
x=&\frac{1}{\sqrt{8}} のとき\\
&y=\log_2 \frac{1}{\sqrt{8}}=\log_2 \frac{1}{\sqrt{2^3}}=\log_2 \frac{1}{2^{\frac{3}{2}}}=\log_2 2^{\tiny{-}\frac{3}{2}}=-\dfrac{3}{2}\log_2 2=-\dfrac{3}{2}
\end{align*}
$$

これらの点をなめらかに結ぶとことによって、対数 $${y=\log_2 x}$$ のグラフが得られます。

このグラフの上に、底の値を変えた $${y=\log_3 x\hspace{-4pt}}$$(赤)と $${y=\log_4 x\hspace{-4pt}}$$(青)のグラフを重ねて描いてみましょう。いずれも右肩上がりのグラフで点 $${(1, 0)}$$ を通ります。その点 $${(1, 0)}$$ の前後で、グラフの上下関係が逆になります。

また、$${y=\log_{\frac{1}{2}}x\hspace{-4pt}}$$(黒)、$${y=\log_{\frac{1}{3}}x\hspace{-4pt}}$$(赤)、$${y=\log_{\frac{1}{4}}x\hspace{-4pt}}$$(青)のグラフも重ねて描いてみます。
例えば、$${y=\log_{\frac{1}{2}}x}$$ のグラフは次の各点を通ります。計算には<底の変換公式>を用います。
$$
\begin{align*}
x=&16 のとき\\
&y=\log_{\frac{1}{2}}16=\hspace{-5pt}\underset{底を 2 に変換}{\dfrac{\log_2 16}{\log_2 \frac{1}{2}}}\hspace{-5pt}=\dfrac{\log_2 2^4}{\log_2 2^{-1}}=\dfrac{4\log_2 2}{-\log_2 2}=\dfrac{4}{-1}=-4\\
x=&8 のとき\\
&y=\log_{\frac{1}{2}}8=\dfrac{\log_2 8}{\log_2 \frac{1}{2}}=\dfrac{\log_2 2^3}{\log_2 2^{-1}}=\dfrac{3\log_2 2}{-\log_2 2}=\dfrac{3}{-1}=-3\\
x=&4 のとき\\
&y=\log_{\frac{1}{2}}4=\dfrac{\log_2 4}{\log_2 \frac{1}{2}}=\dfrac{\log_2 2^2}{\log_2 2^{-1}}=\dfrac{2\log_2 2}{-\log_2 2}=\dfrac{2}{-1}=-2\\
x=&2 のとき\\
&y=\log_{\frac{1}{2}}2=\dfrac{\log_2 2}{\log_2 \frac{1}{2}}=\dfrac{\log_2 2}{\log_2 2^{-1}}=\dfrac{\log_2 2}{-\log_2 2}=\dfrac{1}{-1}=-1\\
x=&1 のとき\\
&y=\log_{\frac{1}{2}}1=0\footnotesize{(底が 1 のときは 0)}\\
x=&\frac{1}{2} のとき\\
&y=\log_{\frac{1}{2}}{\frac{1}{2}}=1\\
x=&\frac{1}{4} のとき\\
&y=\log_{\frac{1}{2}}\frac{1}{4}=\log_{\frac{1}{2}}{\left(\frac{1}{2}\right)}^2=2\log_{\frac{1}{2}}{\frac{1}{2}}=2\\
x=&\frac{1}{8} のとき\\
&y=\log_{\frac{1}{2}}\frac{1}{8}=\log_{\frac{1}{2}}{\left(\frac{1}{2}\right)}^3=3\log_{\frac{1}{2}}{\frac{1}{2}}=3\\
\end{align*}
$$

いずれも右肩下がりのグラフで点 $${(1, 0)}$$ を通ります。その点 $${(1, 0)}$$ の前後で、グラフの上下関係が逆になります。
なお、$${y=\log_2 x}$$ と $${y=\log_\frac{1}{2} x}$$ のグラフは $${x}$$ 軸に関して線対称になります。$${x}$$ 軸で折り返すと、両者のグラフは重なります。

一般に、$${y=\log_a x}$$ と $${y=\log_\frac{1}{a} x}$$ のグラフは、$${x}$$ 軸に関して線対称になります。
参考までに復習として、指数関数 $${y=a^x}$$ と $${y={\left(\frac{1}{a}\right)}^x}$$ のグラフは、$${y}$$ 軸に関して線対称になります(中学でも分かる④「指数関数」)。
例えば、$${y=2^x}$$ と $${y={\left(\frac{1}{2}\right)}^x}$$ のグラフは次のようになります。

あらためて、対数関数は次のように定義されます。
<対数関数の定義>
$${0< a<1}$$ または $${1< a}$$ のとき、実数 $${x}$$ と正の実数 $${y (>0)}$$ について、対数の定義より
$$
\begin{align*}
y=a^x \Longleftrightarrow x=\log_a y
\end{align*}
$$
ここで、$${x=\log_a y}$$ について $${x}$$ と $${y}$$ を入れ替えると
$$
\begin{align*}
y=\log_a x
\end{align*}
$$
この関数 $${y=\log_a x}$$ を、$${a}$$ を底とする $${x}$$ の対数関数という。ただし、底 $${a}$$ については
$${0< a<1}$$ または $${1< a}$$(底の条件)
対数 $${x}$$ については
$${x>0}$$(真数条件)
を満たす。
対数関数のグラフは次にようになる。
(case1) $${0< a<1}$$ のとき
(case2) $${1< a}$$ のとき
で場合分けをする。

***
例えば、底 $${a}$$ について
(case1) $${a=\dfrac{1}{2}}$$ のとき
(case2) $${a=2}$$ のとき
のグラフを描くと、次のようになります。

対数関数のグラフの性質
対数関数 $${y=\log_a x}$$ のグラフには次の性質があります。
1.定義域($${x}$$ の範囲)は正の実数全体、値域($${y}$$ の範囲)は実数全体です。

2.$${0< a <1}$$ のとき、$${x}$$ の値が増加すると $${y}$$ の値は減少します。
$${a>1}$$ のとき、$${x}$$ の値が増加すると $${y}$$ の値は増加します。

3.グラフは必ず点 $${(1, 0)}$$ を通り、$${y}$$ 軸に近づいていきます。この近づいていく直線を漸近線といいます。
なお、近づいていくだけで、どこまで近づいても $${y}$$ 軸と接しないことに注意しましょう。

常用対数
$${10}$$ を底とする対数を常用対数といいます。例えば
$${\log_{10} 2}$$
$${\log_{10} x}$$
などが常用対数です。以下、その常用対数の計算例です。
$$
\begin{align*}
&\log_{10} 0.001=\log_{10} 10^{-3}=-3\log_{10} 10=-3\\
&\log_{10} 0.01=\log_{10} 10^{-2}=-2\log_{10} 10=-2\\
&\log_{10} 0.1=\log_{10} 10^{-1}=-\log_{10} 10=-1\\
&\log_{10} 1=0\\
&\log_{10} 10=1\\
&\log_{10} 100=\log_{10} 10^2=2\log_{10} 10=2\\
&\log_{10} 1000=\log_{10} 10^3=3\log_{10} 10=3
\end{align*}
$$
真数が $${10}$$ 倍になると、対数はちょうど $${1}$$ ずつ増えていきます。
表にすると、真数 $${u}$$ に対する常用対数 $${\log_{10} u}$$ の値は
$$
\def\arraystretch{1.5}
\begin{array}{c|c|c|c|c|c|c|c}
u & 0.001 & 0.01 & 0.1 & 1 & 10 & 100 & 1000 \\ \hline
\log_{10} u & -3 & -2 & -1 & 0 & 1 & 2 & 3\\
\end{array}
$$
常用対数表
常用対数表とは、$${\log_{10} u}$$ で示される対数と真数 $${u}$$ の値の対応表で、真数 $${u}$$ の小数第2位まで値が分かれば、小数点以下4桁の $${\log_{10} u}$$ の値が調べられるようになっています。
$${1.0}$$ 以上 $${10}$$ 未満の数値に対する常用対数表を(参考2)で示し、以下はその一部です。
常用対数表(一部)

常用対数表には左端に $${1.0, 1.1, 1.2}$$ といった順で真数の「上から2桁」の数値が並べられています。そして、上端に並んでいる $${0~9}$$ の数字が真数の「小数第2位」の数値です。この縦と横の組み合わせ(行と列の重なる位置)によって示されている数値がその常用対数の値です
例えば、$${\log_{10} 2.16}$$ の場合は、縦方向に「上から2桁の $${\bm{2.1}}$$」、横方向に「小数点第2位の $${\bm{6}}$$」を見つけて、行と列が重なる位置の値を読みます。

すると、この常用対数表の矢印から $${.3345}$$ となるため、$${\log_{10} 2.16}$$ の値は
$$
\begin{align*}
\log_{10} 2.16=0.3345
\end{align*}
$$
と分かります。
対数が考案されたのは1600年代のはじめ、電卓もパソコンもない時代です。対数の発見により、大きな数の計算を効率的に行えるようになりました。
大きな数の計算をするさい、先に習った次の性質が威力を発揮します。
<対数の重要性質2>(再掲)
$${a}$$ については、$${0< a<1}$$ または $${1< a}$$(底の条件)
$${M}$$ については、$${M>0}$$(指数条件)
$${N}$$ については、$${N>0}$$(指数条件)
で、$${p}$$ が実数のとき
1. $${\log_a MN=\log_a M+\log_a N}$$
2. $${\log_a \dfrac{M}{N}=\log_a M-\log_a N}$$
3. $${\log_a M^p=p\log_a M}$$
特に、$${M=a}$$ のときは
4. $${\log_a a^p=p\log_a a=p}$$
***
それでは常用対数表を用いて、大きな数の計算を具体的に行ってみましょう。
大きな数のかけ算を常用対数で求める
3桁のかけ算
$${223\times654}$$
を考えます。そのためには、先に習った<対数の重要性質2>の 1.
1. $${\log_a MN=\log_a M+\log_a N \cdots (*11)}$$
を用います。
$${2.23}$$ の常用対数 $${\log_{10} 2.23}$$ の値は、縦に $${2.2}$$、横に $${3}$$ を取ることによって、下表の矢印より
$$
\begin{align*}
\log_{10} 2.23=0.3483 \cdots (*12)
\end{align*}
$$

すると
$${223=2.23\times100=2.23\times10^2}$$
より、$${223}$$ の常用対数をとると
$$
\begin{align*}
\log_{10} 223&=\log_{10}(2.23\times10^2)\\
&=\log_{10} 2.23+\log_{10} 10^2 \cdots (*11) より\\
&=\log_{10} 2.23+2\log_{10} 10\\
&=0.3483+2 \cdots (*12) より\\
&=2.3483 \cdots (*13)
\end{align*}
$$
また、$${6.54}$$ の常用対数 $${\log_{10} 6.54}$$ の値は、縦に $${6.5}$$、横に $${4}$$ を取ることによって、下表の矢印より
$$
\begin{align*}
\log_{10} 6.54=0.8156 \cdots (*14)
\end{align*}
$$
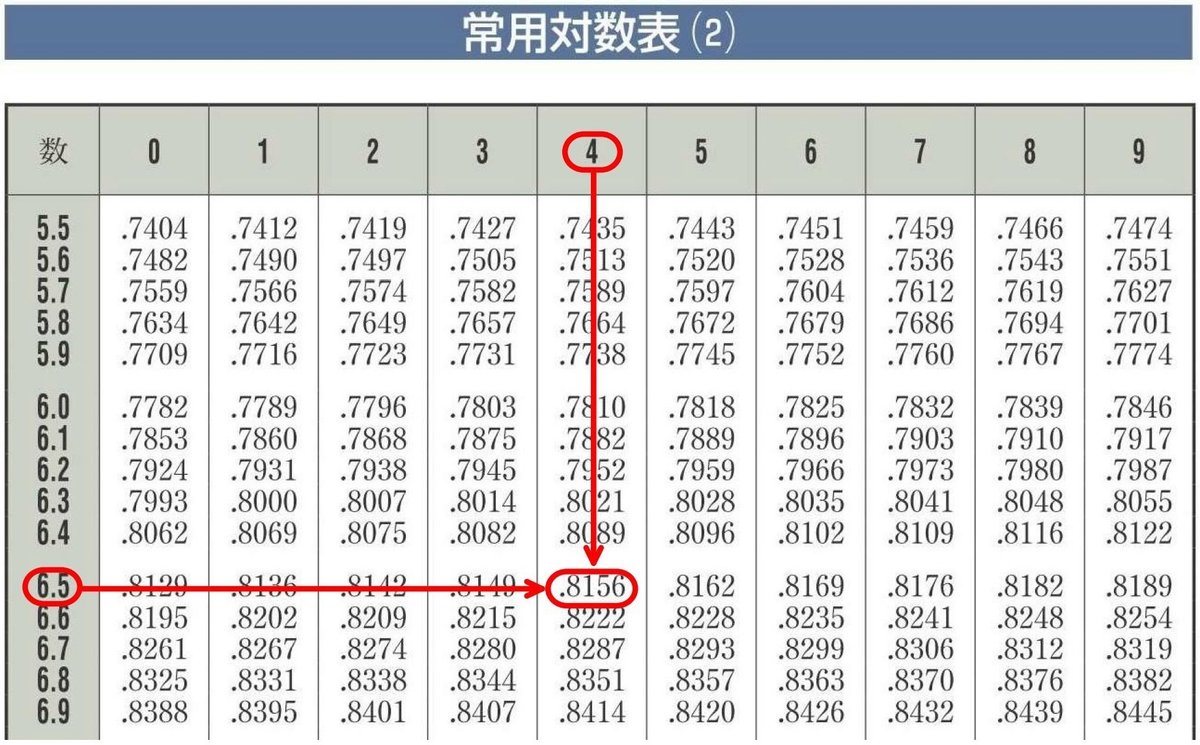
すると
$${654=6.54\times100=6.54\times10^2}$$
より、$${654}$$ の常用対数をとると
$$
\begin{align*}
\log_{10} 654&=\log_{10}(6.54\times10^2)\\
&=\log_{10} 6.54+\log_{10} 10^2 \cdots (*11) より\\
&=\log_{10} 6.54+2\log_{10}10\\
&=0.8156+2 \cdots (*14) より\\
&=2.8156 \cdots (*15)
\end{align*}
$$
よって
$$
\begin{align*}
\log_{10}(223\times654)&=\log_{10}223+\log_{10}654 \cdots (*11) より\\
&=2.3483+2.8156 \cdots (*13), (*15) より\\
&=5.1639\\
&=0.1639+5 \cdots (*16)
\end{align*}
$$
$${(*11)}$$ により、かけ算の計算が、より簡単なたし算の計算にすり替わっていることに着目しましょう。かけ算よりたし算の方が計算は簡単です。これが対数の発見により、天文学の膨大な計算が簡単に行えるようになった理由です。
次は、常用対数表を逆にたどり、常用対数の値から真数を求めます。つまり、対数 $${\log_{10} u}$$ の値から真数 $${u}$$ を求めます。
$${0.1639}$$ の値を常用対数表から見つけますが、同じ値がないときは最も近い値を選択します。一番近い値は $${0.1644}$$ です。下図の矢印(青)より、縦列「上から2桁が $${\bm{1.4}}$$」、横列「小数点第2位が $${\bm{6}}$$」なので
$$
\begin{align*}
0.1639=\log_{10} 1.46 \cdots (*17)
\end{align*}
$$

すると、$${5=5\log_{10}10=\log_{10}10^5}$$ なので
$$
\begin{align*}
(*16)&=0.1639+5\\
&=\log_{10} 1.46+\log_{10} 10^5 \cdots (*17) より\\
&=\log_{10}(1.46\times10^5) \cdots (*11) より\\
&=\log_{10} 146000
\end{align*}
$$
より
$$
\begin{align*}
\log_{10}(223\times675)=\log_{10} 146000
\end{align*}
$$
よって、真数部分だけを比較して
$$
\begin{align*}
223\times675=146000
\end{align*}
$$
となります。実際の計算結果は
$${223\times675=150525}$$
と、その誤差は
$${150525-146000=4525}$$
程度の値が得られました。精度を高めるためにはより細かい対数表が必要です。小数点以下さらに多くの桁数の常用対数表を使用すれば、より正確な数値が求められることになります。
対数の発見
対数の発見者は、スコットランドの数学者、物理学者、天文学者であるジョン・ネイピアといわれています。1614 年、ネイピアはその対数を用いた対数表を発表しました。

対数はかけ算をたし算に、わり算をひき算に、累乗をかけ算に変えるので、巨大な数の計算が、対数を使うと容易になります。つまり、次の<対数の重要性質2>です。
$$
\begin{align*}
\log_a{\underset{\tiny かけ算}{MN}}&=\log_a{M}\hspace{-4pt}\underset{\tiny たし算}{+}\hspace{-3pt}\log_a{N}\\
\log_a{\underset{\tiny わり算}{\dfrac{M}{N}}}&=\log_a{M}\hspace{-3pt}\underset{\tiny ひき算}{-}\hspace{-4pt}\log_a{N}\\
\log_a \underset{\tiny 累乗}{M^p}&=p\hspace{-4pt}\underset{\tiny かけ算}{\times}\hspace{-4pt}\log_a M
\end{align*}
$$
時は大航海時代。ヨーロッパ各国が新天地に向けて船を漕ぎ出した時代です。天体観測によって船の位置や方角を算出するのに、当時の天文学者は巨大な数の計算に苦労していました。彼らの計算を助けるために対数に目を向けたネイピアは、計算を簡略化するための対数表を20年もの年月をかけて完成させたのです。
当時の科学者には、この対数が魔法のような計算に思えたでしょう。天文学の膨大な計算を簡単に行えるようにした対数について、フランスの数学者、物理学者、天文学者であるピエール゠シモン・ラプラス(1749 - 1827)は「対数は天文学者の寿命を 2 倍にした」と賞賛しています。
常用対数表の作成
イングランドの数学者ヘンリー・ブリッグス(Henry Briggs)は、対数を発明したジョン・ネイピアと検討を繰り返し、それまでのネイピアの対数表を改良して1624年、小数点以下14桁まで計算された常用対数の対数表(常用対数表)を作成しました。
常用対数は「常用」と付されているように、地震の規模を表すマグニチュードや、酸や塩基の程度を示す pH(ペーハー)、音の大きさを表すデシベルの計算などに使われています。
(参考1)数の分類
数の分類は以下の通りです。
$$
\begin{align*}
\boldsymbol{複素数 a+bi}
\begin{cases}
\overset{\small b=0 のとき}{\boldsymbol{実数 a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数} \scriptsize{(1, 2, 3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数} \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
{\footnotesize 例 0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize(循環する無限小数)}}\\
{\footnotesize 例 0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
{\scriptsize 例 \pi (=3.1415\cdots) のような \boldsymbol{循環しない無限小数}}\\
{\scriptsize e (=2.7182\cdots) のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0 のとき}{\boldsymbol{虚数 a+bi}} 特に a=0 のとき \boldsymbol{bi} を\boldsymbol{純虚数}という。
\end{cases}
\end{align*}
$$
(参考2)常用対数表


いいなと思ったら応援しよう!

