
もっと分かりやすく①「累乗根の添加」
5次方程式に解の公式が存在しないことについて、重要な概念である「累乗根の添加」をもう一度概説します。ここでは馴染みのある2次方程式を中心に述べていきます。3次方程式も5次方程式も、その延長で議論できます。
まずは1次方程式から始めます。
1次方程式の解の公式が存在すること
1次方程式
$${ax+b=0}$$
を考えます。中学高校生でも分かるように、係数 $${a, b}$$ の範囲を有理数とします(注1)(注2)。有理数とは、例えば
$${\dfrac{3}{2}}$$、$${-\dfrac{4}{5}}$$
のように分数で表される数のことです。なお、整数 $${3}$$ や $${-5}$$ なども
$${3=\dfrac{3}{1}}$$、$${-5=-\dfrac{5}{1}}$$
と分数で表せるので有理数です。なお、1次方程式なので $${a\ne0}$$ です。
これを $${x}$$ について解くと、まず $${b}$$ を移項して
$${ax=-b}$$(移項すると符号が変わる)
両辺を $${a(\ne0)}$$ で割って
$${\dfrac{\cancel{a}x}{\cancel{a}}=-\dfrac{b}{a}}$$(両辺を同じ数で割っても等号は成立)
より
$${x=-\dfrac{b}{a}}$$
つまり、これが1次方程式の解の公式です。簡単に求まるので覚えるまでもないですが、これを1次方程式の解の公式として与えることは可能です。
すると、この公式
$${x=-\dfrac{b}{a}}$$
は、係数と我々が普通に使っている数(以下、中学高校生でも分かるように有理数とします)の加減乗除 ($${\small +, -, \times, \div}$$) で表されています。あえて丁寧に書くと
$${x=-\dfrac{b}{a}=-1\times(b\div a)}$$
と表すことができ、有理数 $${-1}$$ と係数 $${a, b}$$ の加減乗除で解の公式は構成されています。ここで意識しておきたいのは
「1次方程式の解の公式は、係数 $${a, b}$$ と有理数の加減乗除で構成可能である」
ということです。
$${x=-\dfrac{b}{a}=\overset{有理数 \atop \downarrow}{-1}\hspace{-8pt}\underset{\uparrow \atop かけ算}{\times}\hspace{-6pt}(\hspace{-4pt}\overset{係数 \atop \downarrow}{b}\hspace{-9pt}\underset{\uparrow \atop わり算}{\div}\hspace{-9pt}\overset{係数 \atop \downarrow}{a}\hspace{-4pt})}$$
ここで、今後のために集合という概念を導入します。数学的な意味での集合とは「範囲のはっきりしたものの集まり」です。そして集合を作っている個々のものを、その集合の要素といいます(注3)。例えば、自然数の集合や、60の正の約数の集合などが、数学的な意味での集合となります。
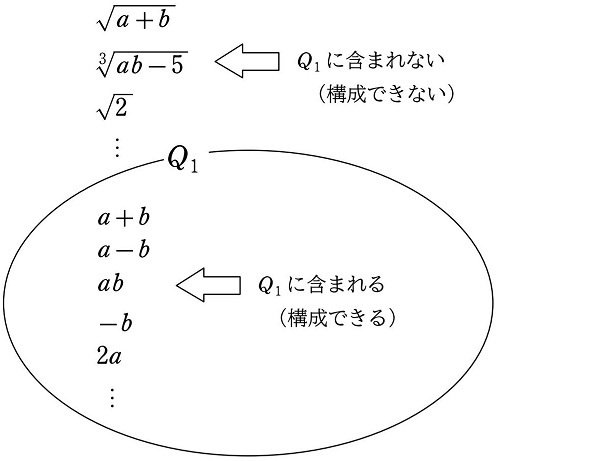
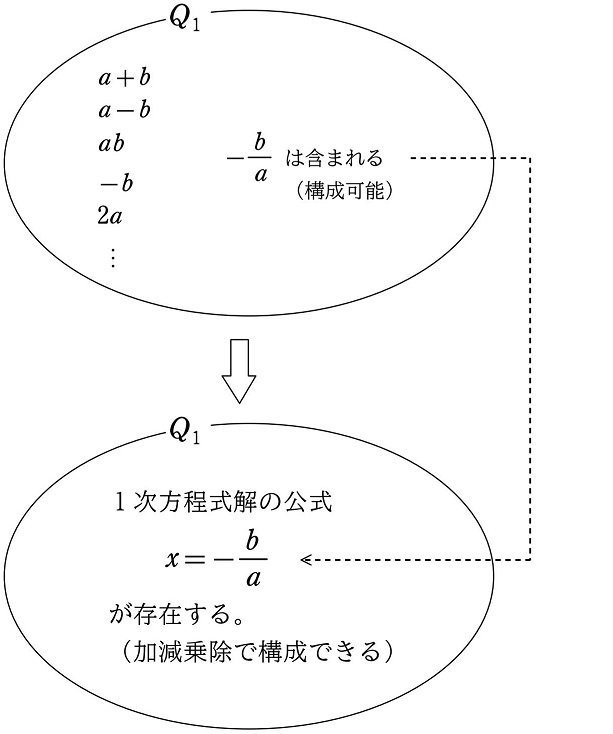
ここで次のような集合を考えます。1次方程式 $${ax+b=0}$$ について
$${Q_1=\hspace{-5pt}}$${1次方程式の係数 $${a, b}$$ と有理数の加減乗除で構成できるすべての式の集合}
例えば、集合 $${Q_1}$$ には次のような式が含まれます。
$${a+b}$$(たし算)
$${a-b}$$(ひき算)
$${ab (=a\times b)}$$(かけ算)
$${2a (=2\times b)}$$(かけ算)
$${-b (=-1\times b)}$$(かけ算)
$${a-4b}$$(かけ算とひき算)
$${\dfrac{a}{3b}(=a\div(3\times b))}$$(かけ算とわり算)
$${a^2-b+\dfrac{3ab}{2}}$$(加減乗除)
$${a}$$(1文字の式も含みます)
$${3}$$(ただの整数も含みます)
$${-\dfrac{5}{2}}$$(ただの有理数も含みます)
$${a^2}$$($${a\times a}$$ なので平方(2乗)も含みます)
この様な式が無数に含まれています。
逆に、以下のように累乗根の入った式や数は $${Q_1}$$ に含まれません。
$${\sqrt{a+b}}$$(平方根)
$${\sqrt[3]{ab+5}}$$(3乗根)
$${\sqrt{2}}$$(無理数)
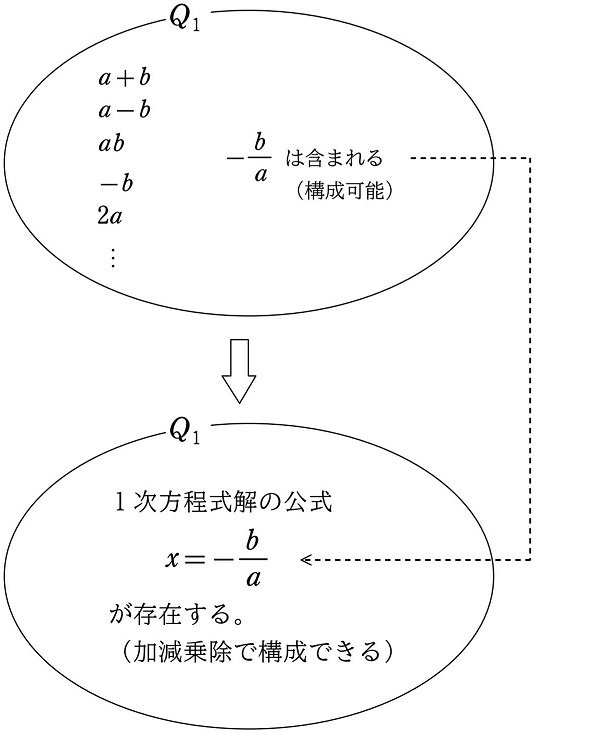
すると、先ほど導いた1次方程式の解の公式
$${x=-\dfrac{b}{a}}$$
は
$${x=-\dfrac{b}{a}=-1\times(b\div a)}$$
と、有理数 $${-1}$$ と係数 $${a, b}$$ の加減乗除で構成できるので、集合 $${Q_1}$$ の中に存在します。見方を変えれば、1次方程式の解の公式は、集合 $${Q_1}$$ の中で加減乗除だけで構成可能であるということです。
解の公式が「存在する」ことの証明は、実際に式変形で作りだせれば証明できます。しかし「存在しない」ことの証明は、式変形の方法は無限にあるので、それとは違う視点が必要になります。
そこで、解の公式が構成できる枠(集合)に着目します。解の公式が構成できる集合が存在すれば、解の公式が存在するといえる。しかし5次方程式では、解の公式が構成できる集合は存在しない。よって、5次方程式には解の公式が存在しない。これを証明していくのが本シリーズでの目標となります。
2次方程式の解の公式が存在すること
それでは次に、2次方程式の場合を考えます。2次方程式
$${ax^2+bx+c=0}$$
について、解の公式は次のようなものでした。なお、中学高校生でも分かるように、係数 $${a, b, c}$$ の範囲を有理数とします(注2)。
$${x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$$
このように、2次方程式には解の公式が存在します。なお、解の公式が存在するとは、解の公式を「加減乗除 ($${\small +, -, \times, \div}$$) と累乗根 ($${\scriptsize \sqrt{ }, \sqrt[3]{ }, \cdots}$$) を用いて構成できる」ということです。2次方程式の解の公式は、平方根を用いて構成できます。
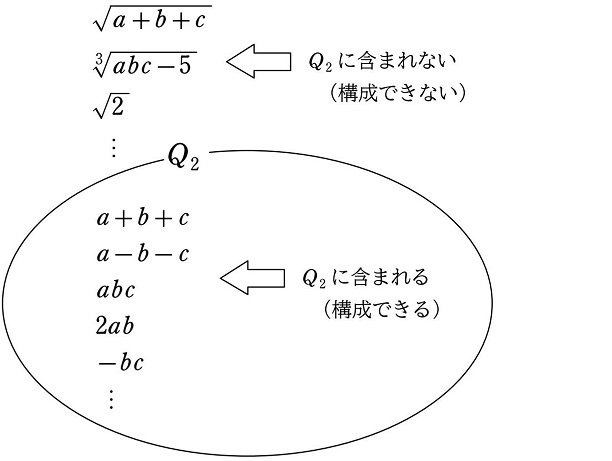
ここで、1次方程式のときと同様に、次のような集合 $${Q_2}$$ を考えます。2次方程式 $${ax^2+bx+c=0}$$ について
$${Q_2=\hspace{-5pt}}$${2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で構成できるすべての式の集合}
例えば、集合 $${Q_2}$$ には次のような式が含まれます。新たに文字 $${c}$$ が加わっているだけで、1次方程式のときと同じ理屈です。
$${a+b+c}$$(たし算)
$${a-b-c}$$(ひき算)
$${abc}$$(かけ算)
$${2ab}$$(かけ算)
$${-bc}$$(かけ算)
$${a-4b+3c}$$(かけ算とひき算)
$${\dfrac{ac}{3b}}$$(かけ算とわり算)
$${a^2-bc+\dfrac{3ab}{2}}$$(加減乗除)
$${a}$$(1文字の式も含みます)
$${3}$$(ただの整数も含みます)
$${-\dfrac{5}{2}}$$(ただの有理数も含みます)
$${a^2}$$($${c\times c}$$ なので平方(2乗)も含みます)
逆に、以下のように累乗根の入った式や数は $${Q_2}$$ に含まれません。
$${\sqrt{a+b+c}}$$(平方根)
$${\sqrt[3]{abc-5}}$$(3乗根)
$${\sqrt{2}}$$(無理数)
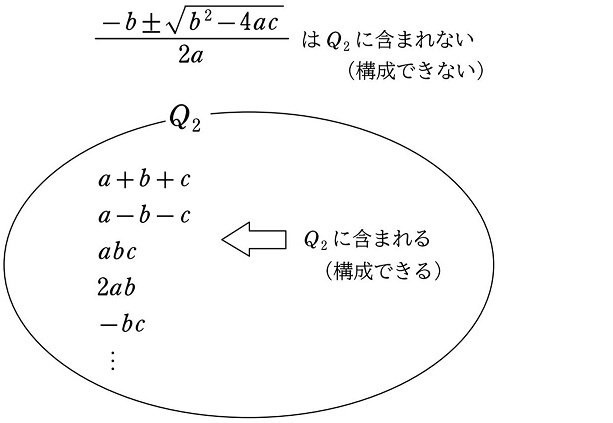
すると、2次方程式の解の公式
$${x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$$
は、集合 $${Q_2}$$ の中で構成可能ではありません。なぜなら、この公式の平方根の部分
$${\sqrt{b^2-4ac}}$$
は、$${Q_2}$$ の中で構成可能ではないからです。$${a^2}$$ のように、平方(2乗)はかけ算なので、$${Q_2}$$ の中で構成可能です。しかし平方根(ルートを取る操作)は、加減乗除のみが許された $${Q_2}$$ の中では構成可能ではありません。
そこで、本記事のテーマである「累乗根の添加」という概念が重要になってきます。2次方程式の場合は平方根の添加です。
ここで2次方程式の解の公式の導出を復習しておきましょう。導出の過程において、どこで平方根が登場するのかを確認します。
(復習)2次方程式の解の公式の導出
2次方程式 $${ax^2+bx+c=0}$$ について、$${x^2}$$ の係数を $${1}$$ にするために両辺を $${a(\ne 0)}$$ で割って
$$
\begin{gather*}
ax^2+bx+c=0\\
x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0
\end{gather*}
$$
ここで平方完成をします。$${x}$$ の係数 $${\dfrac{b}{a}}$$ の半分、つまり $${2}$$ で割った $${\dfrac{b}{2a}}$$ の $${2}$$ 乗 $${\left(\dfrac{b}{2a}\right)^2}$$ を左辺に足して引きます。同じものを足して引いたので、式の等号は成り立ちます。
$$
\begin{align*}
x^2+\frac{b}{a}x\underbrace{+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2}_{足して引いた}+\dfrac{c}{a}&=0\\
\underline{x^2+2\cdot\frac{b}{2a}x+\left(\frac{b}{2a}\right)^2}-\left(\frac{b}{2a}\right)^2+\dfrac{c}{a}&=0
\end{align*}
$$
すると $${x^2+2Ax+A^2=(x+A)^2}$$ の因数分解公式を利用すれば、$${A}$$ を $${\dfrac{b}{2a}}$$ と見立てることによって、下線部は
$$
\begin{align*}
&x^2+2\hspace{10pt}A\hspace{3pt}x+\hspace{8pt}A^2\hspace{11pt}=\hspace{3pt}(\hspace{1pt}x+\hspace{2pt}A\hspace{1pt})^2\\
&x^2+2\cdot\dfrac{b}{2a}x+\left(\dfrac{b}{2a}\right)^2=\left(x+\dfrac{b}{2a}\right)^2
\end{align*}
$$
と因数分解できるので、下線部を $${\left(x+\dfrac{b}{2a}\right)^2}$$ と因数分解して
$$
\begin{gather*}
\left(x+\dfrac{b}{2a}\right)^2-\left(\dfrac{b}{2a}\right)^2+\dfrac{c}{a}=0
\end{gather*}
$$
$${-\left(\dfrac{b}{2a}\right)^2+\dfrac{c}{a}}$$ を右辺に移項して
$$
\begin{align*}
\left(x+\dfrac{b}{2a}\right)^2&=\left(\dfrac{b}{2a}\right)^2-\dfrac{c}{a}\\
&=\left(\dfrac{1}{2}\cdot\dfrac{b}{a}\right)^2-\dfrac{c}{a}\\
&=\left(\dfrac{1}{2}\right)^2\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}\\
&=\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
\end{align*}
$$
より
$$
\begin{align*}
\left(x+\dfrac{b}{2a}\right)^2&=\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a} \cdots ①
\end{align*}
$$
ここで、両辺の平方恨をとって
$$
\begin{gather*}
x+\dfrac{b}{2a}=\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ②
\end{gather*}
$$
となります。平方根をとると $${\pm}$$ と、プラスマイナスの符号が現れることに注意してください。
$${x^2=4}$$ の解は $${x=\pm\sqrt{4}=\pm2}$$
$${x^2=5}$$ の解は $${x=\pm\sqrt{5}}$$
と、プラスマイナスがつくのと同じ考え方です。
ここで $${\dfrac{b}{2a}}$$ を移項して
$$
\begin{gather*}
x=-\dfrac{b}{2a}\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ③
\end{gather*}
$$
あとはこの式を整理して
$$
\begin{align*}
x&=-\dfrac{b}{2a}\pm\sqrt{\dfrac{1}{4}\left\{\left(\dfrac{b}{a}\right)^2-4\cdot\dfrac{c}{a}\right\}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\left(\dfrac{b}{a}\right)^2-4\cdot\dfrac{c}{a}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\dfrac{b^2}{a^2}-\dfrac{4c}{a}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\dfrac{b^2}{a^2}-\dfrac{4ac}{a^2}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\dfrac{b^2-4ac}{a^2}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\cdot\dfrac{\sqrt{b^2-4ac}}{\sqrt{a^2}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\cdot\dfrac{\sqrt{b^2-4ac}}{a}\\
&=-\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}\\
&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$
これで、教科書に載っている形での2次方程式の解の公式が得られました。この導出過程を見ると、$${①}$$ から $${②}$$ の過程で平方根が必要なことがわかります。再掲すると
(再掲)
$$
\begin{align*}
\left(x+\dfrac{b}{2a}\right)^2&=\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a} \cdots ①
\end{align*}
$$
ここで、両辺の平方恨をとって
$$
\begin{gather*}
x+\dfrac{b}{2a}=\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ②
\end{gather*}
$$
の部分です。2次方程式の解の公式を求めるためには、上記のように平方根を取る操作が必要です。
ここで、あらためて $${①}$$ の右辺
$${\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}$$
を見てください。この右辺の式は2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で計算できるので、集合 $${Q_2}$$ の中で構成可能な式です。よって集合 $${Q_2}$$ の中では $${①}$$ までは計算可能です。しかし $${②}$$ の右辺は、平方根を取る操作が含まれているので $${Q_2}$$ の中で構成できません。

そこで「添加」という概念が必要です。$${②}$$ の右辺(のプラスの方)
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ④}$$
を添加して式の集合を拡大します。加減乗除できる仲間として、新たに $${④}$$ を追加するわけです。平方根
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
を加減乗除できる仲間として $${Q_2}$$ に添加し、添加されたその集合を $${Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$
とします。すると、$${Q_2}$$ に含まれる $${-\dfrac{b}{2a}}$$ と新たに添加された
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
の加減乗除によって、2次方程式の解の公式の導出過程に現れた $${③}$$ の右辺
$$
\begin{gather*}
-\dfrac{b}{2a}\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
\end{gather*}
$$
が構成できます。これを $${x=}$$ として、先ほどの(復習)2次方程式の解の公式の導出のように計算していけば、教科書でも馴染みのある形で2次方程式の解の公式
$${x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$$
が得られます。2次方程式の解の公式は、この拡大された集合
$${Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$
の中で構成可能となるわけです。なお、添加について(注4)でさらに詳しく解説します。
以上が、2次方程式に解の公式が存在することの理由です(本シリーズ (11))(注5)。


なお、添加する式は
「$${Q_2}$$ で構成できる式の平方根」
でなければなりません。$${Q_2}$$ で構成できなければ、どこからその式を持ってきたのかということになります。実際 $${①}$$ 式の右辺
$${\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}$$
は、集合 $${Q_2}$$ 内で構成可能です。いわばこれは旧種の式です。そして新種の式である、その平方根
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
を $${Q_2}$$ に添加することによって、その拡大された集合
$${Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$
内で、いよいよ2次方程式の解の公式が構成できるようになる(よって解の公式が存在する)と結論できるのです。
なお、1次方程式では、係数 $${a, b}$$ と有理数との加減乗除のみで解の公式が構成できるため、集合 $${Q_1}$$ の中で解の公式が構成でき、 新種の式を添加する必要ありませんでした。
しかし、2次方程式は、集合 $${Q_2}$$ に平方根
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
の添加が必要でした。このように、必要な累乗根の添加によって、3次方程式、4次方程式の解の公式は構成されます。
解の公式が存在するということは、まず初めに「係数と有理数の加減乗除で表されるすべての式の集合」を与え、平方根、3乗根と必要な段階まで累乗根を添加していきます。ただし、平方根、3乗根ならなんでもよいというわけではなく、添加する前の集合内で構成できる式の平方根、3乗根です。
その平方根、3乗根を添加することによって構成可能な式の集合を次々と拡大し、どこかの段階でその集合内で解の公式が構成できるようになる、というのが、解の公式が存在することのベースの考え方となります。
3次方程式の解の公式が存在すること
3次方程式 $${ax^3+bx^2+cx+d=0}$$ の解の公式は次のようなものでした。
$$
{\begin{align*}
x= \begin{cases}
-\dfrac{b}{3a}+\sqrt[3]{
-\dfrac{q}{2}+\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
+\sqrt[3]{
-\dfrac{q}{2}-\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}\\
-\dfrac{b}{3 a}+\omega \sqrt[3]{
-\dfrac{q}{2}+\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
+\omega^{2} \sqrt[3]{
-\dfrac{q}{2}-\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}\\
-\dfrac{b}{3a}+\sqrt[3]{
-\dfrac{q}{2}+\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
+\sqrt[3]{
-\dfrac{q}{2}-\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
\end{cases}
\end{align*}}
$$
ただし
$$
{\begin{align*}
p&=-\frac{1}{3}\left(\frac{b}{a}\right)^{2}+\frac{c}{a}\\
q&=\frac{2}{27}\left(\frac{b}{a}\right)^{3}-\frac{1}{3}\left(\frac{b}{a}\right)\left(\frac{c}{a}\right)+\frac{d}{a}
\end{align*}}
$$
非常に複雑な式ですが、$${x}$$ の中に $${p}$$ と $${q}$$ があります。その $${p}$$ と $${q}$$ は2次方程式の係数 $${a, b, c, d}$$ を用いてあらかじめ計算できるので、その値を先に求めてから $${x}$$ に代入すれば解が求まります。$${x}$$ は3通りあるので、これが3次方程式の3つの解となります。
すると、3次方程式の解の公式には、3乗根 $${\sqrt[3]{\hspace{10pt}}}$$ の中に平方根 $${\sqrt{\hspace{10pt}}}$$ があることに気付きます。これの意味することは、3次方程式の解の公式を得るためには、平方根と3乗根が必要だということです(本シリーズ (10))。
詳しくは本シリーズ (12)、(13) でとなりますが、3次方程式の解の公式は、係数と有理数と定数 $${\omega}$$ の加減乗除で構成できるすべての式の集合に、まずは適当な平方根($${\sqrt{(X_3)^2}}$$)を添加し、構成できる式の集合を拡大します。さらにその集合に、適当な式の3乗根($${\sqrt[3]{A^3}}$$)を添加して、構成できる式の集合をさらに拡大、その拡大された最後の集合内で、3次方程式の解の公式は構成可能となります。
3次方程式の解の公式が存在するところまで、構成できる式の集合(加減乗除で使える式の集合)を拡大するわけです。

なお、上図の $${X_3}$$ は、3次方程式の解 $${\alpha, \beta, \gamma}$$ の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\beta)}$$
であり、$${A}$$ はラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
となります(本シリーズ (12)、(13)) 。
また、4次方程式の解の公式は本シリーズでは述べませんでしたが、3次方程式のときと同様に、3乗根の添加までで解の公式が構成可能となります。
5次方程式に解の公式が存在しないこと
5次方程式では、平方根(差積)の添加までは可能ですが、それ以上適当な式の添加は不可能である、とするのがアーベルの証明(アーベル・ルフィニの定理)の結論となります。
もし5次方程式に解の公式が存在するとすれば、3次方程式のときと同様に、例えば平方根、3乗根、5乗恨と次々と累乗根を添加することによって、拡大されたどこかの集合内で解の公式が構成できると期待されます。しかし添加できるのは平方根まで、それ以上は適当な式を添加できないので、5次方程式には解の公式は存在しない、というのがアーベルの証明(アーベル・ルフィニの定理)の概要です(本シリーズ (14)~(17))。
5次方程式の解の公式が存在するところまで、構成できる式の集合(加減乗除で使える式の集合)は拡大できません。

なお、上図の $${X_5}$$ は、5次方程式の解 $${x_1, x_2, x_3, x_4, x_5}$$ の差積
$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$
となります(本シリーズ (14))。
ただ、このことを数学的に証明するには、もう一つの重要なテーマである解の置換による「対称性の破壊」に言及する必要があります。
累乗根の添加で構成可能な式の集合が拡大するにつれて、その集合内の式の対称性が破壊(縮小)されていく。そして最終的に対称性(その集合内のすべての式を変化させない置換)を恒等置換にまで破壊することができれば、その拡大された最後の集合内で解の公式が構成可能となる、というのがそれです。「累乗根の添加」と「対称性の破壊」をリンクさせることが、5次方程式に解の公式が存在しないことの証明に必要です(本シリーズ (14)~(17))。
「対称性の破壊」についての概要は、次の記事にしたいと思います。
(注1)数の分類
数の分類は以下の通りです。
$$
\begin{align*}
\boldsymbol{複素数 a+bi}
\begin{cases}
\overset{\small b=0 のとき}{\boldsymbol{実数 a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数} \scriptsize{(1, 2, 3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数} \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
{\footnotesize 例 0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize(循環する無限小数)}}\\
{\footnotesize 例 0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
{\scriptsize 例 \pi (=3.1415\cdots) のような \boldsymbol{循環しない無限小数}}\\
{\scriptsize e (=2.7182\cdots) のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0 のとき}{\boldsymbol{虚数 a+bi}} 特に a=0 のとき \boldsymbol{bi} を\boldsymbol{純虚数}という。
\end{cases}
\end{align*}
$$
(注2)係数は複素数まで拡張することは可能
1次方程式
$${ax+b=0}$$
の係数 $${a, b}$$ は複素数まで拡張することは可能ですが、中学高校では有理数の範囲で係数を扱うことが多いので、それにならって係数は有理数で考えるのが分かりやすいと思います。
同じ理由で、本シリーズにおける2次方程式
$${ax^2+bx+c=0}$$
の係数 $${a, b, c}$$ も有理数、さらには3次方程式など、それ以上の高次方程式の係数も、(複素数まで拡張できますが)有理数の範囲で考えるのが分かりやすいと思います。
本文では係数の範囲を具体的に明示していませんでしたが、分かりやすさを優先して有理数としておきます(後で本文で補足を入れる予定)。有理数で理解できれば、係数が複素数のときにも自然に拡張できると思います(これについて必要性が出てくれば、そのときに解説をします)。
(注3)集合の概念について
集合の概念を扱うことで、中身(要素)が無限にある集合でも、数学的対象として扱いやすくなります。
例えば、自然数の集合は記号で $${\mathbb{N}}$$ と表しますが、$${3}$$ は自然数なので、集合 $${\mathbb{N}}$$ の中に含まれる( $${3}$$ は $${\mathbb{N}}$$ の要素である)ことを
$${3 \in \mathbb{N}}$$
と記号で表記できます。一方、$${\dfrac{3}{2}}$$ は自然数ではないので、集合 $${\mathbb{N}}$$ の中に含まれない($${\dfrac{3}{2}}$$ は $${\mathbb{N}}$$ の要素ではない)ことを
$${\dfrac{3}{2} \notin \mathbb{N}}$$
と表記できます。無限にある集合を、輪郭のある”袋”(自然数 $${\mathbb{N}}$$ という袋)のようなイメージでとらえることができるので、その袋に入っている、入っていないで、厳密な数学的議論が可能になります。

なお、その当時はまだ集合の概念が無かったためか、集合を用いないで書かれているアーベルの原論分は、冒頭から分かりにくいものになっているようです。その分かりにくい部分を本シリーズのように集合で補って考えれば、証明の輪郭がはっきりすると思います。
なお、本シリーズは次の教科書(特に前者の方)を最も参照しています。
『不可能の証明』(津田文夫著)
『代数学講義』(高木貞治著)
この教科書ではアーベルの証明(アーベル・ルフィニの定理)を、集合を用いて現代風に解説しています。
(注4)添加についてもっと詳しく
本文に何度も出てくる「累乗根の添加」ついて、もう少し詳しく述べます。
まずは有理数の集合を考えてみましょう。
有理数とは、$${\dfrac{2}{3}, \dfrac{5}{1}}$$ のように分数で表せる数でした。有理数の特徴として、「有理数同士で加減乗除を行っても有理数である」という性質があります。
有理数 $${+}$$ 有理数 $${=}$$ 有理数
有理数 $${-}$$ 有理数 $${=}$$ 有理数
有理数 $${\times}$$ 有理数 $${=}$$ 有理数
有理数 $${\div}$$ 有理数 $${=}$$ 有理数
具体例で確認してみます。2つの有理数 $${\dfrac{3}{2}}$$ と $${\dfrac{1}{5}}$$ について、加減乗除をそれぞれ計算してみると
$${\dfrac{3}{2}+\dfrac{1}{5}=\dfrac{15}{10}+\dfrac{2}{10}=\dfrac{17}{10}}$$(有理数)
$${\dfrac{3}{2}-\dfrac{1}{5}=\dfrac{15}{10}-\dfrac{2}{10}=\dfrac{13}{10}}$$(有理数)
$${\dfrac{3}{2}\times\dfrac{1}{5}=\dfrac{3\times1}{2\times5}=\dfrac{3}{10}}$$(有理数)
$${\dfrac{3}{2}\div\dfrac{1}{5}=\dfrac{3}{2}\times\dfrac{5}{1}=\dfrac{3\times5}{2\times1}=\dfrac{15}{2}}$$(有理数)
このように、有理数同士は加減乗除を行っても有理数です。このことを「有理数の集合は加減乗除で閉じている」といいます。
この、加減乗除で閉じた集合のことを『体(たい)』といいます。つまり、有理数の集合は体です。
では、整数の集合は加減乗除で閉じているでしょうか?整数 $${2}$$ と $${5}$$ で計算してみると
$${2+5=10}$$(整数)
$${2-5=-3}$$(整数)
$${2\times5=10}$$(整数)
$${2\div5=\dfrac{2}{5}=0.4}$$(整数ではない)
より、整数同士のわり算は常に整数とはならないので、加減乗除で閉じてはいません。つまり、整数の集合は体ではありません。
ここで、有理数の集合を $${\mathbb{Q}}$$ とします。この有理数の集合に、有理数ではない(無理数である) $${\sqrt{2}}$$ を添加し、拡大された式の集合を $${\mathbb{Q}(\sqrt{2})}$$ とします。いわば旧種の数である有理数の集合に、新種の数である $${\sqrt{2}}$$ を、加減乗除の”仲間”に加えるわけです。

ここで、添加とは
「加減乗除で閉じた集合の範囲を拡大すること」
を意味します。もともと加減乗除で閉じた有理数の集合(体)があり、それに新しい数 $${\sqrt{2}}$$ を添加して得られる、有理数と $${\sqrt{2}}$$ の加減乗除で閉じた集合が $${\mathbb{Q}(\sqrt{2})}$$ となります。この集合のことを、拡大された体という意味で『拡大体』といいます。
すると、拡大体 $${\mathbb{Q}(\sqrt{2})}$$ に含まれるのは次のような数です。
もともと $${\mathbb{Q}}$$ に含まれる数(つまり有理数)はそのまま $${\mathbb{Q}(\sqrt{2})}$$ に含まれます。
$${2}$$(整数)
$${-1}$$(整数)
$${\dfrac{3}{2}}$$(有理数)
$${-\dfrac{1}{4}}$$(有理数)
また下記のように、有理数と $${\sqrt{2}}$$ との加減乗除で得られる数も $${\mathbb{Q}(\sqrt{2})}$$ に含まれます。
$${2+\sqrt{2}}$$
$${1-\sqrt{2}}$$
$${-4+3\sqrt{2}}$$
$${5\sqrt{2}}$$
$${\dfrac{1}{3}-\dfrac{2}{5}\sqrt{2}}$$
$${\sqrt{2}}$$(添加した数そのもの)

なお、$${\mathbb{Q}(\sqrt{2})}$$に含まれる式は、$${s, t}$$ を有理数として
$${s+t\sqrt{2}}$$
という形で書くことができます。上の例はすべてそのような形で表されています。
例えば整数 $${2}$$ は、$${s=2, t=0}$$ とすれば得られます。
$${s+t\sqrt{2}=2+0\cdot\sqrt{2}=2}$$
添加した $${\sqrt{2}}$$ そのものは、$${s=0, t=1}$$ とすれば得られます。
$${s+t\sqrt{2}=0+1\cdot\sqrt{2}=\sqrt{2}}$$
もちろん $${2+3\sqrt{2}}$$ は、$${s=2, t=3}$$ とすればOKです。
$${s+t\sqrt{2}=2+3\cdot\sqrt{2}=2+3\sqrt{2}}$$
では、$${2+3\sqrt{2}}$$ と $${5-\sqrt{2}}$$ について、その加減乗除をそれぞれ計算してみましょう。加減乗除で閉じているので、足しても引いても掛けても割っても、その結果は $${s, t}$$ を有理数として
$${s+t\sqrt{2}}$$
という同じ形で表されるはずです。この形で書けなければ $${\mathbb{Q}(\sqrt{2})}$$ に含まれません。例えば、$${s+t\sqrt{3}}$$ や $${s+t\sqrt{2}+u\sqrt{3}}$$ のような形になると、それは $${\mathbb{Q}(\sqrt{2})}$$ には含まれなくなります。
では、実際に計算してみると
$$
\begin{align*}
&\begin{align*}
(2+3\sqrt{2})+(5-\sqrt{2})&=2+3\sqrt{2}+5-\sqrt{2}\\
&=2+5+3\sqrt{2}-\sqrt{2}\\
&=7+(3-1)\sqrt{2}\\
&=7+2\sqrt{2} (\mathbb{Q}(\sqrt{2}) に含まれる)
\end{align*}\\
&\begin{align*}
(2+3\sqrt{2})-(5-\sqrt{2})&=2+3\sqrt{2}-5+\sqrt{2}\\
&=2-5+3\sqrt{2}+\sqrt{2}\\
&=-3+(3+1)\sqrt{2}\\
&=-3+4\sqrt{2} (\mathbb{Q}(\sqrt{2}) に含まれる)
\end{align*}\\
&\begin{align*}
(2+3\sqrt{2})(5-\sqrt{2})&=2\cdot5-2\cdot\sqrt{2}+3\sqrt{2}\cdot5-3\sqrt{2}\cdot\sqrt{2}\\
&=10-2\sqrt{2}+15\sqrt{2}-3\cdot(\sqrt{2})^2\\
&=10-2\sqrt{2}+15\sqrt{2}-3\cdot2((\sqrt{2})^2=2 より)\\
&=10-2\sqrt{2}+15\sqrt{2}-6\\
&=10-6-2\sqrt{2}+15\sqrt{2}\\
&=4+(15-2)\sqrt{2}\\
&=4+13\sqrt{2} (\mathbb{Q}(\sqrt{2}) に含まれる)
\end{align*}\\
&\begin{align*}
\dfrac{2+3\sqrt{2}}{5-\sqrt{2}}&=\dfrac{(2+3\sqrt{2})(5+\sqrt{2})}{(5-\sqrt{2})(5+\sqrt{2})} (分母の有利化)\\
&=\dfrac{2\cdot5+2\cdot\sqrt{2}+3\sqrt{2}\cdot5+3\sqrt{2}\cdot\sqrt{2}}{5^2-(\sqrt{2})^2} \cdots (*)\\
&=\dfrac{10+2\sqrt{2}+15\sqrt{2}+3(\sqrt{2})^2}{25-2}\\
&=\dfrac{10+2\sqrt{2}+15\sqrt{2}+3\cdot2}{23}\\
&=\dfrac{10+2\sqrt{2}+15\sqrt{2}+6}{23}\\
&=\dfrac{10+6+2\sqrt{2}+15\sqrt{2}}{23}\\
&=\dfrac{16+(2+15)\sqrt{2}}{23}\\
&=\dfrac{16+17\sqrt{2}}{23}\\
&=\dfrac{16}{23}+\dfrac{17}{23}\sqrt{2} (\mathbb{Q}(\sqrt{2}) に含まれる)
\end{align*}
\end{align*}
$$
よって、どれも $${s, t}$$ を有理数として
$${s+t\sqrt{2}}$$
の形で表されるので、集合 $${\mathbb{Q}(\sqrt{2})}$$ は加減乗除で閉じていることが分かります。今は1回の計算のみ確認しましたが、どのような複雑な計算でも、一つ一つの加減乗除の連続で計算されるので、最終的な結果はやはり $${s+t\sqrt{2}}$$ の形で表されます。
なお $${(*)}$$ の分母では展開公式
$${(a+b)(a-b)=a^2-b^2}$$
を利用しています。
ここで、2次方程式のところで述べた集合 $${Q_2}$$ を確認しましょう。
$${Q_2=\hspace{-5pt}}$${2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で構成できるすべての式の集合}
この集合は加減乗除で閉じているので体になります。2次方程式の解の公式では、この集合 $${Q_2}$$ に
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
を添加して、構成可能な式の集合を
$${Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$
に拡大します。この拡大された式の集合(拡大体)の中では
$$
\begin{gather*}
x=-\dfrac{b}{2a}\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ③
\end{gather*}
$$
という式が構成できます。これを変形していけば、教科書で馴染みのある2次方程式の解の公式が得られます。
このようにして、2次方程式の解の公式が存在することを、「平行恨の添加による体の拡大」という新しい視点をもって理論づけることができます。
(注5)本シリーズとの違い
本シリーズ (11) では、2次方程式
$${ax^2+bx+c=0}$$
について、両辺を $${a\ne0}$$ で割って
$$
\begin{align*}
\dfrac{ax^2+bx+c}{a}&=\dfrac{0}{a}\\
\dfrac{ax^2}{a}+\dfrac{bx}{a}+\dfrac{c}{a}&=0\\
x^2+\dfrac{b}{a}x+\dfrac{c}{a}&=0
\end{align*}
$$
$${\dfrac{b}{a}=a_1, \dfrac{c}{a}=a_2}$$ と置いて
$$
\begin{align*}
x^2+a_1x+a_2=0
\end{align*}
$$
とし、2乗の係数を $${1}$$ としました。ここで、最初に考える加減乗除で閉じた集合を
$${Q=}$${係数 $${a_1, a_2}$$ と有理数の加減乗除で表されるすべての式の集合}
とし、この式に平方根 $${\sqrt{(a_1)^2-4a_1}}$$ を添加して・・・、という流れで本篇は議論しています。
こうすると、3つの係数の文字 $${a, b, c}$$ を $${a_1, a_2}$$ と2つに減らすことができ、今後の議論の見通しがよくなります。
なお添加する式は、2次方程式の解 $${\alpha, \beta}$$ の差積 $${X_2}$$ の平方根
$${\sqrt{(X_2)^2}=\sqrt{(\alpha-\beta)^2}}$$
を添加することと同じとなります(本シリーズ (11) )。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベント」による「3次方程式の解の公式」の導出
(8)「偶置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となることを解説
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「偶置換」にまで絞り込む(破壊する)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(破壊する)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から偶置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、偶置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての偶置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点的に解説
