
<アーベルの証明(終)>任意の3次巡回置換は5次巡回置換の積で表せること
(初めに)本文は本シリーズ (16) から続いています。初見の場合は本シリーズ (16) から(またはそれ以前から)読んだ方が分かりやすいかと思います。証明としては本記事で最後となります。
スピンオフとして、説明が難しかったと思われる「累乗根の添加」と「対称性の破壊」について、馴染みのある2次方程式を使って、もっと具体的で分かりやすい解説をする予定です。
(本文スタート)
小学5年生の森田君はしばし考えた後、「そうか」と霧が晴れたような表情で口火を切った。
「5次以上の方程式には解の公式は存在しない。今からそれを証明しましょう」
探偵のような口ぶりに、家庭教師の竹村は思わず身を乗り出す。
大まかな証明の流れ
「5次方程式に解の公式が存在しないことについて、大まかな証明の流れは以下のようになります(本シリーズ (14)~(16))。
(step1)
5次方程式に解の公式が存在すると仮定します。詳しく言うと、5次方程式の解の公式を、加減乗除 ($${\small +, -, \times, \div}$$) と累乗根 ($${\scriptsize \sqrt{ }, \sqrt[3]{ }, \cdots}$$) を用いて構成できると仮定します(背理法の仮定)(注1)。
(step2)
次の「条件Ⅰ」
「条件Ⅰ」
『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
『$${X}$$ はある5次置換で変化するが、$${X^2}$$ はすべての5次置換で変化しない。』
を満たす解の式 $${X}$$ を考えます。つまり
$$
\begin{align*}
X &\xrightarrow[\hspace{7pt}ある5次置換\hspace{7pt}]{} 変化する{\small(対称式でない)}\\
X^2 &\xrightarrow[すべての5次置換]{} X^2 変化しない{\small(対称式)}
\end{align*}
$$
この「条件Ⅰ」を満たす解の式 $${X}$$ として、差積 $${X_5}$$
$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$
を取ることができます。$${X_5}$$ は偶置換シンメトリーをもつので、その $${X_5}$$ を加減乗除の仲間に加える(添加する)ことによって、構成可能な式の対称性を、完全なる対称性(対称式)から偶置換シンメトリーまで破壊することができます(本シリーズ (14))。
$$
\begin{gather*}
Q(\omega)\\
\hspace{67pt}\downarrow \Leftarrow X_5 の添加\\
Q(\omega, X_5)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf 5次置換(対称式)}\\
\hspace{67pt}\downarrow \Leftarrow X_5 の添加\\
{\bf 偶置換シンメトリー}
\end{gather*}
$$
しかし、拡大された $${Q(\omega, X_5)}$$ 内では5次方程式の解の公式は構成できません。構成可能な式の対称性はまだ偶置換シンメトリーです。偶置換シンメトリーをさらに破壊し、構成可能な式の対称性(式を変化させない置換)を、解の公式と同等である恒等置換にまで破壊しなければなりません(注2)。よって、次のステップへと進みます。
(step3)
次の「条件Ⅱ」
「条件Ⅱ」
『$${Y}$$ はある偶置換で変化するが、$${Y^3}$$ はすべての偶置換で変化しない(ただし $${Y^3}$$ は対称式ではない)』
を満たす解の式 $${Y}$$ を考えます。つまり
$$
\begin{align*}
Y&\xrightarrow[\hspace{7pt}ある偶置換\hspace{7pt}]{} 変化する{\small(偶置換シンメトリーをもたない)}\\
Y^3 &\xrightarrow[すべての偶置換]{} Y^3 変化しない{\small(偶置換シンメトリー)}
\end{align*}
$$
ここで「すべての偶置換は3次巡回置換または3次巡回置換の積で表され、かつすべての3次巡回置換は偶置換である」ことから、この「条件Ⅱ」の偶置換を3次巡回置換に置き換えることが可能です。
「条件Ⅱ」(3次巡回置換バージョン)
『$${Y}$$ はある3次巡回置換で変化するが、$${Y^3}$$ はすべての3次巡回置換で変化しない(ただし $${Y^3}$$ は対称式ではない)』
つまり
$$
\begin{align*}
Y&\xrightarrow[\hspace{7pt}ある3次巡回置換\hspace{7pt}]{} 変化する{\small(偶置換シンメトリーをもたない)}\\
Y^3 &\xrightarrow[すべての3次巡回置換]{} Y^3 変化しない{\small(偶置換シンメトリー)}
\end{align*}
$$
この $${Y}$$ を $${Q(\omega, X_5)}$$ に添加することによって、3次方程式のときと同様に、使える式の範囲を拡大しつつ、偶置換シンメトリーをさらに破壊していくことが期待できます(注3)(注4)。
$$
\begin{gather*}
Q(\omega)\\
\hspace{67pt}\downarrow \Leftarrow X_5 の添加\\
Q(\omega, X_5)\\
\hspace{67pt}\downarrow \Leftarrow Y の添加\\
Q(\omega, X_5, Y) まで拡大可能か?
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf 5次置換(対称式)}\\
\hspace{67pt}\downarrow \Leftarrow X_5 の添加\\
{\bf 偶置換シンメトリー}\\
\hspace{67pt}\downarrow \Leftarrow Y の添加\\
{\bf 対称性をさらに破壊できるか?}
\end{gather*}
$$
しかし、望みの $${Y}$$ を得ようとすると矛盾が生じます(後述)。矛盾が生じた理由は「5次方程式に解の公式が存在する」と仮定したことです (step1)。よって
(step4) 背理法により、5次方程式に解の公式が存在しないことが証明された。
以上が、5次方程式に解の公式が存在しない証明の大まかな流れです。この証明の意図することは、偶置換シンメトリーを破壊するための望みの $${Y}$$ が得られないので、偶置換シンメトリーをさらに破壊し、構成可能な式の対称性(式を変化させない置換)を、解の公式と同等である恒等置換にまで破壊することはできない(よって5次方程式の解の公式を構成することができない)、ということです(注2)。
なお理解の助けとするために、3次方程式との対比で、5次方程式での証明を眺めてみると、以下のようになります。
$$
\begin{gather*}
{\bf 3次置換(対称式)}\\
\,6 通り\\[4pt]
\hspace{63pt}\downarrow \Leftarrow 差積 X_3 の添加\\[6pt]
{\bf 偶置換シンメトリー}\\
\hspace{4pt}3 通り\\[4pt]
\hspace{60pt}\downarrow \Leftarrow A の添加\\[6pt]
{\bf 恒等置換}\\
\,\,\,1 通り\\
\hspace{2pt}\downarrow\\
{\bf 解の公式が存在する}\\[-48pt]
\end{gather*}
\hspace{0pt}
\begin{gather*}
{\bf 5次方程式では解の公式}\\
{\bf が存在すると仮定する}\hspace{8pt}\\
\hspace{2pt}\downarrow\\
{\bf 5次置換(対称式)}\\
\,120 通り\\[4pt]
\hspace{63pt}\downarrow \Leftarrow 差積 X_3 の添加\\[6pt]
{\bf 偶置換シンメトリー}\\
\hspace{4pt}60 通り\\[-2pt]
\hspace{70pt}\downarrow \Leftarrow {\small Y を得ようと \atop \hspace{-27pt}すると}\\
{\bf 矛盾が起きる}\\[-3pt]
\hspace{2pt}\Updownarrow\\[-1pt]
{\bf これ以上対称性を破壊できない}\\[-2pt]
\hspace{2pt}\downarrow\\[-2pt]
{\bf 解の公式が存在しない(背理法)}
\end{gather*}
$$
<図解>

少し詳しく補足すると、『条件Ⅰ』をみたす解の式である差積 $${X_5}$$ について、その2乗
$$
\begin{align*}
(X_5)^2=\{(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)\}^2&
\end{align*}
$$
は対称式なので、集合 $${Q(\omega)}$$ 内で加減乗除によって構成可能となります(以下、構成可能というのは加減乗除で構成可能という意味)。
しかし、その平方根 $${\sqrt{(X_5)^2}}$$ は $${Q(\omega)}$$ 内では構成可能ではないので、 $${Q(\omega)}$$ に $${\sqrt{(X_5)^2}}$$ を添加して、構成可能な式の集合を $${Q(\omega, \sqrt{(X_5)^2})}$$ へと拡大します。この集合 $${Q(\omega, \sqrt{(X_5)^2})}$$ 内で構成可能な式は、偶置換シンメトリーをもちます。なお
$${\sqrt{(X_5)^2}=X_5, -X_5}$$
より、$${\sqrt{(X_5)^2}}$$ を添加することと $${X_5}$$ を添加することは同じなので(注5)、$${Q(\omega, \sqrt{(X_5)^2})}$$ と $${Q(\omega, X_5)}$$ は同じ集合です。
$${Q(\omega, \sqrt{(X_5)^2})=Q(\omega, X_5)}$$
ここまでは、2次方程式や3次方程式のときと同じストーリーです(注3)(注4)。
しかし集合 $${Q(\omega, X_5)}$$ 内で5次方程式の解の公式は構成可能ではないので、偶置換シンメトリーを破壊すべく『条件Ⅱ』を満たす解の式 $${Y}$$ の添加を試みます。しかし、その $${Y}$$ を得ようとすると矛盾が生じる(その結果として構成可能な式の集合が $${Q(\omega, X_5)}$$ から拡大できず、構成可能な式の対称性を偶置換シンメトリーからさらに破壊できない)ので、5次方程式の解の公式は存在しないということになります。
さて、(step2) まではすでにやりました(本シリーズ (13)~(15))。これから (step3) を証明していきます」
自信あり気な森田君。いよいよ最終段階が始まった。
任意の3次巡回置換を5次巡回置換で表す
「まず、ある公式を導きます。『任意の3次巡回置換は2つの5次巡回置換の積で表すことができる』という公式です。えーっと・・・」
まだ完全に詰め切れていなかったか、森田君はホワイトボードの前で考え込む。竹村の時間も止まる。計算しているのか森田君の指先は小刻みに動く。森田君のペンは動いた。
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
「これでいいはずです。3次巡回置換 $${(x_1 x_2 x_3)}$$ を、2つの5次巡回置換の積で表すことに成功しました。これを $${①}$$ とします。後ほど詳しく述べますが、この $${①}$$ を用いることによって、 (step3) で示した矛盾を導くことができます。
では $${①}$$ を証明するために、文字列
$${x_1 x_2 x_3 x_4 x_5}$$
に、$${①}$$ の両辺を作用させてみます。
(左辺)=$${(x_1 x_2 x_3)}$$
は
$${x_1 \rightarrow x_2 \rightarrow x_3 \rightarrow x_1}$$
と、$${x_1}$$ を $${x_2}$$ に、 $${x_2}$$ を $${x_3}$$ に、$${x_3}$$ を $${x_1}$$ に巡回的に入れ替える置換なので、左辺を作用させると
$$
\begin{align*}
x_1 x_2 &x_3 x_4 x_5\\
&\Downarrow (x_1 x_2 x_3) を作用\\
x_2 x_3 &x_1 x_4 x_5 (*1)
\end{align*}
$$
一方
(右辺)$${=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1)}$$
について、5次巡回置換 $${(x_5 x_4 x_3 x_2 x_1)}$$ は
$${x_5 \rightarrow x_4 \rightarrow x_3 \rightarrow x_2 \rightarrow x_1 \rightarrow x_5}$$
と、$${x_5}$$ を $${x_4}$$ に、 $${x_4}$$ を $${x_3}$$ に、$${x_3}$$ を $${x_2}$$ に、$${x_2}$$ を $${x_1}$$ に、 $${x_1}$$ を $${x_5}$$ に巡回的に入れ替える置換であり、かつ5次巡回置換 $${(x_3 x_4 x_5 x_2 x_1)}$$ は
$${x_3 \rightarrow x_4 \rightarrow x_5 \rightarrow x_2 \rightarrow x_1 \rightarrow x_3}$$
と、$${x_3}$$ を $${x_4}$$ に、 $${x_4}$$ を $${x_5}$$ に、$${x_5}$$ を $${x_2}$$ に、$${x_2}$$ を $${x_1}$$ に、$${x_1}$$ を $${x_3}$$ に巡回的に入れ替える置換なので、右辺を作用させると、本シリーズでの定義より置換の積は左から(前から)順に作用させて(注6)
$$
\begin{align*}
x_1 x_2 &x_3 \underline{x_4 x_5}\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4\\
&\Downarrow (x_3 x_4 x_5 x_2 x_1) を作用\\
x_2 x_3 &x_1 \underline{x_4 x_5} (*2)
\end{align*}
$$
より、$${(*1)}$$ と $${(*2)}$$ は同じ並びとなるので、$${①}$$ 式
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
が成り立つことが証明されます。$${①}$$ の右辺を作用させても最終的に $${x_4}$$ と $${x_5}$$ は変化せず(下線部)、$${(x_1, x_2, x_3)}$$ の巡回置換だけが残ることがポイントです」
「どうやって気付いたの?」竹村は思わずたずねた。
「まず、5次巡回置換はすべての解を入れ替える置換なので、次のような5次巡回置換
$${(x_5 x_4 x_3 x_2 x_1)}$$
を考えます。添え字の数が大きい順にならぶ置換です。これを文字列
$${x_1 x_2 x_3 x_4 x_5}$$
に作用させると、次のように1つずつずれていきます。
$$
\begin{align*}
x_1 x_2 &x_3 x_4 x_5\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4
\end{align*}
$$
さらに、ある5次巡回置換 $${(\bigcirc \triangle \square \raisebox{2pt}{▽} ◎)}$$ によって、$${(*4)}$$ のように変化したとします(下図)。
$$
\begin{align*}
x_1 x_2 &x_3 \underline{x_4 x_5} (*3)\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4\\
&\Downarrow (\bigcirc \triangle \square \raisebox{2pt}{▽} ◎) を作用\\
♤ \,♢ &\,♡ \underline{x_4 x_5} (*4)
\end{align*}
$$
3次巡回置換 $${(x_1 x_2 x_3)}$$ は、ここに現れない $${x_4}$$ と $${x_5}$$ を変化させないので、$${(*3)}$$ から $${(*4)}$$ にかけて $${x_4}$$ は $${x_4}$$ のまま、$${x_5}$$ は $${x_5}$$ のままで固定します(下線部)。
さて、ここから5次巡回置換 $${(\bigcirc \triangle \square \raisebox{2pt}{▽} ◎)}$$ を決定していきます。
まず、$${(*3)}$$ から $${(*4)}$$ にかけて3次巡回置換 $${(x_1 x_2 x_3)}$$ となる必要があるので、$${x_1}$$ が $${x_2}$$ に置き換わるよう、$${♤}$$ を $${x_2}$$ にします。
$$
\begin{align*}
\underline{x_1} x_2 &x_3 x_4 x_5 (*3)\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4\\
&\Downarrow (\bigcirc \triangle \square \raisebox{2pt}{▽} ◎) を作用\\
\underline{x_2} \,♢ &\,♡ x_4 x_5 (*4)
\end{align*}
$$
$${(*3)}$$ から $${(*4)}$$ にかけて、$${x_1}$$ が $${x_2}$$ に置き換わっていることが確認できます(下線部)。さらに $${x_2}$$ が $${x_3}$$ に置き換わるよう、$${♢}$$ を $${x_3}$$ にします。
$$
\begin{align*}
x_1 \underline{x_2} &x_3 x_4 x_5 (*3)\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4\\
&\Downarrow (\bigcirc \triangle \square \raisebox{2pt}{▽} ◎) を作用\\
x_2 \underline{x_3} &\,♡ x_4 x_5 (*4)
\end{align*}
$$
$${(*3)}$$ から $${(*4)}$$ にかけて、$${x_2}$$ が $${x_3}$$ に置き換わっていることが確認できます(下線部)。最後に $${x_3}$$ が $${x_1}$$ に置き換わるよう $${♡}$$ を $${x_1}$$ にして
$$
\begin{align*}
x_1 x_2 &x_3 x_4 x_5 (*3)\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4 (**3)\\
&\Downarrow (\bigcirc \triangle \square \raisebox{2pt}{▽} ◎) を作用\\
x_2 x_3 &x_1 x_4 x_5 (*4)
\end{align*}
$$
ここで $${(*4)}$$ 列を確認すると、途中の $${(**3)}$$ から $${(*4)}$$ にかけて
$${x_3 \rightarrow x_4 \rightarrow x_5 \rightarrow x_2 \rightarrow x_1 \rightarrow x_3}$$
と巡回的に置換されていることがわかります。よって、5次巡回置換 $${(\bigcirc \triangle \square \raisebox{2pt}{▽} ◎)}$$ は
$${(x_3 x_4 x_5 x_2 x_1)}$$
と決まり、下図のように確定します。
$$
\begin{align*}
x_1 x_2 &x_3 x_4 x_5\\
&\Downarrow (x_5 x_4 x_3 x_2 x_1) を作用\\
x_5 x_1 &x_2 x_3 x_4\\
&\Downarrow (x_3 x_4 x_5 x_2 x_1) を作用\\
x_2 x_3 &x_1 x_4 x_5
\end{align*}
$$
先ほどやった $${(*2)}$$ と同じ結果です。これは $${(x_1 x_2 x_3)}$$ と同じ置換なので、作用させた5次巡回置換を左から順に並べて
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
となり、 $${(x_1 x_2 x_3)}$$ を5次巡回置換の積で表すことができました。最初に逆に並べた5次巡回置換
$${(x_5 x_4 x_3 x_2 x_1)}$$
によって文字の列を1つずつずらした後、次の5次巡回置換
$${(x_3 x_4 x_5 x_2 x_1)}$$
によって $${x_4, x_5}$$ を最初の位置に戻し、最後に3次巡回置換
$${(x_1 x_2 x_3)}$$
だけが残るという仕組みです。
なお、他の文字を使ってどのような3次巡回置換を持ってきても、必ず5次巡回置換の積で表すことができます」
森田君はすらすらと書き並べる。
(例)
$$
\begin{align*}
(x_1 x_2 x_4)&=(x_5 x_3 x_4 x_2 x_1)(x_4 x_3 x_5 x_2 x_1)\\
(x_1 x_2 x_4)&=(x_5 x_3 x_4 x_2 x_1)(x_4 x_3 x_5 x_2 x_1)\\
(x_2 x_5 x_4)&=(x_3 x_1 x_4 x_5 x_2)(x_4 x_1 x_3 x_5 x_2)
\end{align*}
$$
「なにか法則性はあるの?」$${①}$$ のみ専門書で用意していた竹村はふと質問した。
「はい。この公式は一般的に次のように構成します。具体的に最初に述べた $${(x_1 x_2 x_3)}$$ について解説します。
任意の3次巡回置換を5次巡回置換の積で表す一般的な構成方法
(step1)
$${(x_1 x_2 x_3)}$$ について、使っていない文字は $${x_4}$$ と $${x_5}$$ です。それを下の $${(*5)}$$ のように、添え字の数の小さい順に $${(x_1 x_2 x_3)}$$ の右横に並べます。添え字の数の順番はどのような順でもよいですが、簡単のため小さい順に並べると分かりやすいです。
$${(x_1 x_2 x_3)\hspace{-37pt}\underset{\overset{\small \uparrow}{\small \raisebox{-8pt}{使っていない文字を並べる}}}{\underline{x_4 x_5}}\hspace{-32pt}\cdots (*5)}$$
(step2)
最初に作用させる5次巡回置換は、この $${(*5)}$$ の並びを、逆の順にして並べます。
$${\hspace{76pt}(x_1 x_2 x_3) x_4 x_5 \cdots (*5)}$$
$${\hspace{116pt}\downarrow {\small 逆に並べる}}$$
$${(x_1 x_2 x_3)=\underset{}{(\underline{x_5 x_4 x_3 x_2 x_1})}(* * * * *)}$$
(step3)
次に作用させる5次巡回置換については、まず後ろ2つの文字を、前の5次巡回置換と同じ文字にします。
$${(x_1 x_2 x_3)=(x_5 x_4 x_3 \underline{x_2 x_1})(* * * \underline{x_2 x_1})}$$
$${\hspace{145pt}\raisebox{5pt}{|}\hspace{-2.8pt}{\over \hspace{82pt}}\hspace{-3.9pt}\raisebox{4.5pt}{↑}}$$
$${\hspace{137pt}\raisebox{10pt}{\small 下線部を同じ文字にする}}$$
(step4)
最後に $${* * *}$$ 部分は
$${(x_1 x_2 x_3)=(\underline{x_5 x_4 x_3} x_2 x_1)(* * * x_2 x_1)}$$
の下線部の順を、逆にしたものを並べます。
$${(x_1 x_2 x_3)=(\underline{x_5 x_4 x_3} x_2 x_1)(\underline{x_3 x_4 x_5} x_2 x_1) \cdots ①}$$
$${\hspace{102pt}\raisebox{5pt}{|}\hspace{-2.8pt}{\over \hspace{86pt}}\hspace{-3.9pt}\raisebox{4.5pt}{↑}}$$
$${\hspace{88pt}\raisebox{10pt}{\small 下線部の順を逆にして並べる}}$$
これで $${①}$$ の完成となります。もう1つ具体例で実践しましょう。
例えば $${(x_2 x_5 x_4)}$$ について実践すると
(step1)
使っていない文字を並べる
$${(x_2 x_5 x_4) \underline{x_1 x_3} \cdots (*6)}$$
(step2)
$${(*6)}$$ の並びを逆に並べる。
$${\hspace{76pt}(x_2 x_5 x_4) x_1 x_3 \cdots (*6)}$$
$${\hspace{116pt}\downarrow {\small 逆に並べる}}$$
$${(x_2 x_5 x_4)=\underset{}{(\underline{x_3 x_1 x_4 x_5 x_2})}(* * * * *)}$$
(step3)
次の5次巡回置換は、まず後ろ2つの文字を、前の5次巡回置換と同じ文字にする。
$${(x_2 x_5 x_4)=\underset{}{(x_3 x_1 x_4 \underline{x_5 x_2})}(* * * \underline{x_5 x_2})}$$
$${\hspace{145pt}\raisebox{5pt}{|}\hspace{-2.8pt}{\over \hspace{82pt}}\hspace{-3.9pt}\raisebox{4.5pt}{↑}}$$
$${\hspace{137pt}\raisebox{10pt}{\small 下線部を同じ文字にする}}$$
(step4)
最後に $${* * *}$$ 部分は、下線部
$${(x_2 x_5 x_4)=(\underline{x_3 x_1 x_4} x_5 x_2)(* * * x_5 x_2)}$$
を逆の順に並べて
$${(x_2 x_5 x_4)=(\underline{x_3 x_1 x_4} x_5 x_2)(\underline{x_4 x_1 x_3} x_5 x_2)}$$
$${\hspace{102pt}\raisebox{5pt}{|}\hspace{-2.8pt}{\over \hspace{86pt}}\hspace{-3.9pt}\raisebox{4.5pt}{↑}}$$
$${\hspace{88pt}\raisebox{10pt}{\small 下線部の順を逆にして並べる}}$$
これで完成となります。一般にこの (step1~4) を順に行えば、すべての3次巡回置換を5次巡回置換の積で表すことができます(注7)。よって
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
を、一般に「任意の3次巡回置換を2つの5次巡回置換の積で表す公式」とみることができます。$${x_1, x_2, x_3, x_4, x_5}$$ はいずれも対等なので、いろいろな場合の代表として、$${①}$$ を取り上げているわけです」
「これ今考えたの?」竹村は驚きの声を上げた。
「この公式 $${➀}$$ を用いることによって、「条件Ⅱ」を満たす解の式 $${Y}$$ を得ようとすると矛盾が生じること、つまり望みの $${Y}$$ を添加して偶置換シンメトリーをさらに破壊することはできないことが証明されます。それをもって『5次方程式には解の公式が存在しないこと』が結論されます。以下、具体的に証明していきます。
証明の最終段階
さて、先に述べた大まかな証明の流れは
(step1) 5次方程式に解の公式が存在すると仮定する。
(step2) 「条件Ⅰ」を満たす差積 $${X_5}$$ を添加することによって、構成可能な式の対称性を、対称式から偶置換シンメトリーまで破壊する。
(step3) 偶置換シンメトリーをさらに破壊するために、「条件Ⅱ」を満たす解の式 $${Y}$$ を得ようとすると、$${➀}$$ によって矛盾がおきる。
(step4) よって背理法により、5次方程式に解の公式が存在しないことが証明された。
でした。(step2) まで終えているので、これから (step3) の証明をしていきます。
さて、次の「条件Ⅱ」を満たす解の式 $${Y}$$ を考えます。
「条件Ⅱ」
『$${Y}$$ はある偶置換で変化するが、$${Y^3}$$ はすべての偶置換で変化しない(ただし $${Y^3}$$ は対称式ではない)』
つまり
$$
\begin{align*}
Y&\xrightarrow[\hspace{7pt}ある偶置換\hspace{7pt}]{} 変化する{\small(偶置換シンメトリーをもたない)}\\
Y^3 &\xrightarrow[すべての偶置換]{} Y^3 変化しない{\small(偶置換シンメトリー)}
\end{align*}
$$
ここで「偶置換は3次巡回置換で表すことができ、かつ3次巡回置換は偶置換である」ことから、この条件の偶置換を3次巡回置換に置き換えることが可能です。
「条件Ⅱ」(3次巡回置換バージョン)
『$${Y}$$ はある3次巡回置換で変化するが、$${Y^3}$$ はすべての3次巡回置換で変化しない(ただし $${Y^3}$$ は対称式ではない)』
つまり
$$
\begin{align*}
Y&\xrightarrow[\hspace{7pt}ある3次巡回置換\hspace{7pt}]{} 変化する{\small(偶置換シンメトリーをもたない)}\\
Y^3 &\xrightarrow[すべての3次巡回置換]{} Y^3 変化しない{\small(偶置換シンメトリー)}
\end{align*}
$$
この「条件Ⅱ」(3次巡回置換バージョン)の前半の条件『$${Y}$$ はある3次巡回置換で変化する』ことから、 解の式 $${Y}$$ を変化させるのは、必ずしもすべての3次巡回置換ではなく、少なくとも1つ存在することになります。『$${Y}$$ は”ある”3次巡回置換で変化する』と「ある」という言葉を使っているのはそういう理由です。少なくとも1つ存在すれば、偶置換シンメトリーは破壊されます。
その「ある」3次巡回置換を $${(i j k)}$$ とおきます。すると、その $${(i j k)}$$ による $${Y}$$ の変化は
$${(i j k)Y=\omega Y, \omega^2Y \cdots ②}$$
となることはすでにやりました(本シリーズ (16))。ある3次巡回置を作用させたときの $${Y}$$ の変化は、$${Y}$$ の $${\omega}$$ 倍になるか、$${Y}$$ の $${\omega^2}$$ 倍になるかのどちらかであり、それ以外の変化はありえないということです。
$$
\begin{align*}
Y\xrightarrow[ある (i j k)]{} \omega Y
\end{align*}
$$
または
$$
\begin{align*}
Y\xrightarrow[ある (i j k)]{} \omega^2Y
\end{align*}
$$
ここで、5次方程式 $${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$ の5つの解を
$${x_1, x_2, x_3, x_4, x_5}$$
とし、「条件Ⅱ」(3次巡回置換バージョン)の最初の条件
『$${Y}$$ はある3次巡回置換で変化する』
を満たす「ある」3次巡回置換を $${(x_1 x_2 x_3)}$$ とおきます。5次方程式の解 $${x_1, x_2, x_3, x_4, x_5}$$ はそれぞれ対等で、どの3つを選んでも一般性を失わないので、解の式 $${Y}$$ を変化させる「ある」3次巡回置換を、代表で $${(x_1 x_2 x_3)}$$ とおくわけです。
この3次巡回置換 $${(x_1 x_2 x_3)}$$ を解の式 $${Y}$$ に作用させると、それは $${②}$$ 式
$${(i j k)Y=\omega Y, \omega^2Y \cdots ②}$$
と同じ結果となるので
$$
\begin{align*}
(x_1 x_2 x_3)Y=\omega Y, \omega^2Y \cdots ③
\end{align*}
$$
となります。この式は、ある3次巡回置換 $${(i j k)}$$ を、5次方程式の解を用いて表した $${(x_1 x_2 x_3)}$$ に書き換えただけです。書き換えただけなので結果は同じです。
$$
\begin{align*}
(i j k)Y&=\omega Y, \omega^2Y \cdots ②\\
書き換え\downarrow\hspace{5.8ex}&\hspace{5.7ex}\downarrow{\small 結果は同じ}\\
(x_1 x_2 x_3)Y&=\omega Y, \omega^2Y \cdots ③
\end{align*}
$$
さてここで、任意の5次巡回置換を考えます。任意の5次巡回置換は、必ず偶数個の互換の積で表せるので偶置換です(本シリーズ (15))。
(例)
$$
\begin{align*}
\underset{\footnotesize 5次巡回置換}{\underline{(x_1 x_2 x_3 x_4 x_5)}}=\underset{\footnotesize 偶数個(4個)の互換の積}{\underline{(x_1 x_2)(x_1 x_3)(x_1 x_4)(x_1 x_5)}}
\end{align*}
$$
すると、「条件Ⅱ」の後半の条件
『$${Y^3}$$ はすべての偶置換で変化しない』
ことより、$${Y^3}$$ に任意の偶置換を作用させても変化しません。
$$
\begin{align*}
Y^3 \xrightarrow[\overset{\raisebox{5pt}{\small ↑}}{\small 任意の偶置換}]{} Y^3 {\small(変化しない)}
\end{align*}
$$
つまり $${Y^3}$$ は偶置換シンメトリーをもっています。すると、任意の5次巡回置換は偶置換であったので、偶置換シンメトリーをもつ $${Y^3}$$ は、任意の5次巡回置換を作用させても変化しないことになります。
$$
\begin{align*}
Y^3 \xrightarrow[\overset{\raisebox{5pt}{\small ↑}}{任意の5次巡回置換}]{} Y^3 {\small(変化しない)}
\end{align*}
$$

そこで、$${x_1, x_2, x_3, x_4, x_5}$$ を用いて得られる任意の5次巡回置換を
$$
\begin{align*}
(l m n o p)
\end{align*}
$$
とおきます。つまり、$${l, m, n, o, p}$$ は $${x_1, x_2, x_3, x_4, x_5}$$ のどれかです。
この5次巡回置換を $${Y^3}$$ に作用させることは、数式で
$${(l m n o p)Y^3}$$
と表記しますが、先ほどやったように、$${Y^3}$$ は任意の5次巡回置換で変化しないことから
$$
\begin{align*}
(l m n o p)Y^3=Y^3 \cdots ④
\end{align*}
$$
さらに、置換は $${Y}$$ に作用して指数部分 $${3}$$ は変化させないので
$$
\begin{align*}
(l m n o p)Y^3=\{(l m n o p)Y\}^3 \cdots ⑤
\end{align*}
$$
$${Y^3}$$ に置換を作用させることは、$${Y}$$ に置換を作用させてから3乗することと同じという式です。すると $${⑤=④}$$ より
$$
\begin{align*}
\{(l m n o p)Y\}^3=Y^3
\end{align*}
$$
ここで簡単のため $${(l m n o p)Y=Q}$$ とおくと
$$
\begin{align*}
Q^3=Y^3
\end{align*}
$$
両辺を $${Y^3(\ne0)}$$ で割って(注8)
$$
\begin{align*}
\frac{Q^3}{Y^3}=1
\end{align*}
$$
3乗をまとめて
$$
\begin{align*}
{\left(\frac{Q}{Y}\right)}^3=1
\end{align*}
$$
すると $${\dfrac{Q}{Y}}$$ は3乗して1になる数(1の3乗根)なので
$$
\begin{align*}
\frac{Q}{Y}=1, \omega, \omega^2 \cdots ⑥
\end{align*}
$$
なお、$${\omega}$$ は「3乗して1になる数(1の3乗根)のうち複素数である定数」です。具体的には
$${\omega=\dfrac{-1+\sqrt{3}i}{2} または \dfrac{-1-\sqrt{3}i}{2}}$$
となります(本シリーズ (2))。ここで $${⑥}$$ 式の両辺に $${Y}$$ をかけて
$$
\begin{align*}
\frac{Q}{Y} \times Y=1 \times Y, \omega \times Y, \omega^2 \times Y
\end{align*}
$$
より
$$
\begin{align*}
Q=Y, \omega Y, \omega^2Y
\end{align*}
$$
$${Q=(l m n o p)Y}$$ だったので
$$
\begin{align*}
(l m n o p)Y=Y, \omega Y, \omega^2Y \cdots ➆
\end{align*}
$$
の3通りがありえます。
この式から分かることは、「条件Ⅱ」を満たす解の式 $${Y}$$ に任意の5次巡回置換を作用させると、それは $${Y}$$ そのもので変化しないか、$${Y}$$ の $${\omega}$$ 倍か、$${Y}$$ の $${\omega^2}$$ 倍のいずれかになるということです。
では次に、$${(l m n o p)Y}$$ の行き先が、$${Y, \omega Y, \omega^2Y}$$ のどれになるかを決定する作業に入ります。5次巡回置換は同じものを5回連続作用させると、変化しないで元に戻ります。つまり、5次巡回置換を5回連続作用させる置換は恒等置換となります。
ここで、任意の5次巡回置換 $${(l m n o p)}$$ を5回連続作用させる置換を
$${(l m n o p)^5}$$
と書くと、これは恒等置換なので、「条件Ⅱ」の解の式 $${Y}$$ に作用させても変化しません。つまり
$${(l m n o p)^5Y=Y(変化しない)\cdots ➇}$$
ここまでの話を図式化すると
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(1回目)}\\
{\small 途中は不明 \rightarrow} & ?\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(2回目)}\\
{\small 途中は不明 \rightarrow} & ?\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(3回目)}\\
{\small 途中は不明 \rightarrow} & ?\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(4回目)}\\
{\small 途中は不明 \rightarrow} & ?\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(5回目)}\\
{\small 変化しない \rightarrow} & Y
\end{align*}
$$
より
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (l m n o p)^5 を作用}\\
{\small 変化しない \rightarrow} & Y
\end{align*}
$$
現時点で途中は不明ですが、5回作用させた時点で $${Y}$$ に戻るということです。この $${➇}$$ 式
$${(l m n o p)^5Y=Y \cdots ➇}$$
は常に成り立つ式となります。つまり先ほどの $${➆}$$ 式
$${(l m n o p)Y=Y, \omega Y, \omega^2Y \cdots ➆}$$
において、右辺が $${Y}$$ か $${\omega Y}$$ か $${\omega^2 Y}$$ のどれになるかは、$${➇}$$ を満たすものでなければなりません。
ここで、$${➆}$$ において
(case1) $${(l m n o p)Y=Y}$$ のとき
(case2) $${(l m n o p)Y=\omega Y}$$ のとき
(case3) $${(l m n o p)Y=\omega^2Y}$$ のとき
と場合分けをして、ひとつひとつ確認していきます。先ほどの $${➇}$$ を満たすかどうかを確認します。
(case1) $${(l m n o p)Y=Y}$$ のとき
これは、$${(l m n o p)}$$ を1回作用させても $${Y}$$ は変化しないという式です。このとき、この5次巡回置換 $${(l m n o p)}$$ を $${Y}$$ に5回連続作用させると
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(1回目)}\\
{\small 変化しない \rightarrow} & Y\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(2回目)}\\
{\small 変化しない \rightarrow} & Y\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(3回目)}\\
{\small 変化しない \rightarrow} & Y\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(4回目)}\\
{\small 変化しない \rightarrow} & Y\\
&\Downarrow {\small \leftarrow (l m n o p) を作用(5回目)}\\
{\small 変化しない \rightarrow} & Y
\end{align*}
$$
よって
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (l m n o p)^5 を作用} \\
{\small 変化しない \rightarrow} & Y
\end{align*}
$$
となり、これは、$${➇}$$ 式
$$
\begin{align*}
(l m n o p)^5Y=Y \cdots ➇
\end{align*}
$$
を満たします。よって、(case1)
$${(l m n o p)Y=Y}$$
は正しい結果となります。
(case2) $${(l m n o p)Y=\omega Y}$$ のとき
これは、$${(l m n o p)}$$ を1回作用させると、$${Y}$$ は $${\omega Y}$$ と $${\omega}$$ 倍に変化するという式です。このとき、この5次巡回置換 $${(l m n o p)}$$ を $${Y}$$ に5回連続作用させると
$$
\begin{align*}
& Y\\
{\small \omega 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(1回目)}\\
&\omega Y\\
{\small \omega 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(2回目)}\\
&\omega^2Y\\
{\small \omega 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(3回目)}\\
&\omega^3Y\\
{\small \omega 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(4回目)}\\
&\omega^4Y\\
{\small \omega 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(5回目)}\\
&\omega^5Y
\end{align*}
$$
よって
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (l m n o p)^5 を作用} \\
&\omega^5Y
\end{align*}
$$
より
$$
\begin{align*}
(l m n o p)^5Y=\omega^5Y \cdots ⑨
\end{align*}
$$
ここで、$${\omega}$$ は「3乗して1になる数(1の3乗根)のうち複素数である定数」なので、$${\omega}$$ を3乗すると $${1}$$ になります。
$${\omega^3=1}$$
すると、指数法則『$${a^{m+n}=a^{m} a^{n}}$$($${m, n}$$ は自然数)』を用いると
$${\omega^5=\omega^{3+2}\hspace{-13pt}\underset{\large ↑ \atop 指数法則}{=}\hspace{-13pt}\underset{1}{\underline{\omega^3}}\cdot\omega^2=1\cdot\omega^2=\omega^2}$$
より
$${\omega^5=\omega^2}$$
となるので、これを $${⑨}$$ に代入して
$$
\begin{align*}
(l m n o p)^5Y&=\omega^5Y\\
&=\omega^2Y
\end{align*}
$$
よって
$$
\begin{align*}
(l m n o p)^5Y=\omega^2Y \cdots ➉
\end{align*}
$$
しかし、これは $${➇}$$ 式
$$
\begin{align*}
(l m n o p)^5Y=Y \cdots ➇
\end{align*}
$$
を満たしません。それは、$${\omega}$$ は
$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$ または $${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので、$${➇}$$ と $${➉}$$ は等しくならないからです。
蛇足的ですが、具体的に計算してみると $${➉=➇}$$ より
$${\omega^2 Y=Y}$$
右辺を左辺に移項して
$${\omega^2 Y-Y=0}$$
$${Y}$$ でくくって
$${(\omega^2-1)Y=0}$$
$${Y}$$ は「条件Ⅱ」を満たすので、$${Y \ne 0}$$ より(注8)
$${\omega^2-1=0}$$
因数分解公式『$${a^2-b^2=(a+b)(a-b)}$$』を用いて左辺を因数分解すると
$${\omega^2-1^2=0}$$
より
$${(\omega+1)(\omega-1)=0}$$
よって
$${\omega+1=0}$$ または $${\omega-1=0}$$
となるので
$${\omega=1}$$ または $${-1}$$
となりますが、$${\omega}$$ は「3乗して1になる数(1の3乗根)のうち複素数である定数」、具体的には
$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$ または $${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので、$${➉}$$ は成り立たないことが分かります。
よって、(case2)
$${(l m n o p)Y=\omega Y}$$
は不適となります。
(case3) $${(l m n o p)Y=\omega^2Y}$$ のとき
これは、$${(l m n o p)}$$ を1回作用させると、$${Y}$$ は $${\omega^2Y}$$ と $${\omega^2}$$ 倍に変化するという式です。このとき、この5次巡回置換 $${(l m n o p)}$$ を $${Y}$$ に5回連続作用させると
$$
\begin{align*}
& Y\\
{\small \omega^2 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(1回目)}\\
&\omega^2Y\\
{\small \omega^2 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(2回目)}\\
&\omega^4Y\\
{\small \omega^2 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(3回目)}\\
&\omega^6Y\\
{\small \omega^2 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(4回目)}\\
&\omega^8Y\\
{\small \omega^2 倍} &\Downarrow {\small \leftarrow (l m n o p) を作用(5回目)}\\
&\omega^{10}Y
\end{align*}
$$
よって
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (l m n o p)^5 を作用} \\
&\omega^{10}Y
\end{align*}
$$
より
$$
\begin{align*}
(l m n o p)^5Y=\omega^{10}Y \cdots ⑪
\end{align*}
$$
すると、(case2) でやったように $${\omega^3=1}$$ なので、指数法則によって
$${\omega^{10}=\omega^{3+3+3+1}\hspace{-13pt}\underset{\large ↑ \atop 指数法則}{=}\hspace{-13pt}\omega^3\cdot\omega^3\cdot\omega^3\cdot\omega={(\underset{1}{\underline{\omega^3}})}^3\cdot\omega=1^3\cdot\omega=\omega}$$
より
$${\omega^{10}=\omega}$$
となるので、これを $${⑪}$$ に代入して
$$
\begin{align*}
(l m n o p)^5Y&=\omega^{10}Y\\
&=\omega Y
\end{align*}
$$
よって
$$
\begin{align*}
(l m n o p)^5Y=\omega Y \cdots ⑫
\end{align*}
$$
しかし、これは $${➇}$$ 式
$$
\begin{align*}
(l m n o p)^5Y=Y \cdots ➇
\end{align*}
$$
を満たしません。先ほどと同様、$${\omega}$$ は
$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$ または $${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので、$${➇}$$ と $${⑫}$$ は等しくならないからです。
ここでも蛇足的ですが、具体的に計算してみると $${⑫=➇}$$ より
$${\omega Y=Y}$$
右辺を左辺に移項して
$${\omega Y-Y=0}$$
$${Y}$$ でくくって
$${(\omega-1)Y=0}$$
$${Y}$$ は「条件Ⅱ」を満たすので、$${Y \ne 0}$$ より(注8)
$${\omega-1=0}$$
よって
$${\omega=1}$$
となりますが、先に述べたように $${\omega}$$ は「3乗して1になる数(1の3乗根)のうち複素数である定数」なので、$${⑫}$$ は成り立たないことがわかります。
よって、(case3)
$${(l m n o p)Y=\omega^2 Y}$$
は不適となります。
以上より、(case1) のときのみ成り立ち、$${(l m n o p)Y}$$ の行き先は
$$
\begin{align*}
(l m n o p)Y=Y \cdots ⑬
\end{align*}
$$
とただ1通りに決まります。$${(l m n o p)Y}$$ の行き先は、$${\omega Y}$$ でも $${\omega^2Y}$$ でもななく $${Y}$$ となる。つまり、任意の5次巡回置換 $${(l m n o p)}$$ を作用させても $${Y}$$ は変化しないということです。
ここで最初に示した $${①}$$ 式
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
が登場します。これは「任意の3次巡回置換は5次巡回置換の積で表すことができる」という関係式です。
まず $${①}$$ の左辺をみてみます。これは「ある」3次巡回置換 $${(x_1 x_2 x_3)}$$ です。先にやりましたが、「条件Ⅱ」(3次巡回置換バージョン)
「条件Ⅱ」(3次巡回置換バージョン)
『$${Y}$$ はある3次巡回置換で変化するが、$${Y^3}$$ はすべての3次巡回置換で変化しない(ただし $${Y^3}$$ は対称式ではない)』
を満たす解の式 $${Y}$$ に「ある」3次巡回置換 $${(x_1 x_2 x_3)}$$ を作用させると
$$
\begin{align*}
(x_1 x_2 x_3)Y=\omega Y, \omega^2Y \cdots ③
\end{align*}
$$
となることは先ほど証明しました。
次に $${①}$$ の右辺をみてみます。これは5次巡回置換の積です。先ほど
$$
\begin{align*}
(l m n o p)Y=Y \cdots ⑬
\end{align*}
$$
を証明しました。任意の5次巡回置換 $${(l m n o p)}$$ を作用させても $${Y}$$ は変化しないという式です。
$${(l m n o p)}$$ は任意の5次巡回置換なので、どのような5次巡回置換を持ってきても $${⑬}$$ は成り立ちます。つまり、$${①}$$ の右辺に表れる2つの5次巡回置換を持ってきても $${⑬}$$ は成り立つので
$${(x_5 x_4 x_3 x_2 x_1)Y=Y}$$(変化しない)
$${(x_3 x_4 x_5 x_2 x_1)Y=Y}$$(変化しない)
ここで、$${Y}$$ に $${①}$$ 式
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
の左辺である
$${(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1)}$$
を作用させてみましょう。本シリーズでは置換の積を左から(前から)順に作用させると定義しているので
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (x_5 x_4 x_3 x_2 x_1) を作用}\\
{\small 変化しない \rightarrow} & Y\\
&\Downarrow {\small \leftarrow (x_3 x_4 x_5 x_2 x_1) を作用}\\
{\small 変化しない \rightarrow} & Y
\end{align*}
$$
より
$$
\begin{align*}
& Y\\
&\Downarrow {\small \leftarrow (x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) を作用}\\
{\small 変化しない \rightarrow} & Y
\end{align*}
$$
よって
$$
\begin{align*}
(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1)Y=Y \cdots ⑭
\end{align*}
$$
となります。ここで $${③}$$ と $${⑭}$$ を並べてみます。
$$
\begin{align*}
(x_1 x_2 x_3)Y&=\omega Y, \omega^2Y \cdots ③\\
(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1)Y&=Y\hspace{32pt} \cdots ⑭
\end{align*}
$$
すると、おかしいことに気付きます。改めて $${①}$$ を確認すると
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
ですが、$${①}$$ の左辺を $${Y}$$ に作用させると $${③}$$ になります。一方、$${①}$$ の右辺を $${Y}$$ に作用させると $${⑭}$$ になります。等しい置換を作用させているので、$${③}$$ と $${⑭}$$ は等しくならないといけません。つまり
$$
\begin{align*}
(x_1 x_2 x_3)Y=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1)Y
\end{align*}
$$
より $${③=⑭}$$ ですが、$${③}$$ は $${\omega Y}$$ または $${\omega^2Y}$$ の2通りがあるので
$$
\begin{align*}
\omega Y=Y または \omega^2Y=Y
\end{align*}
$$
すると、$${Y\ne0}$$ なので
$$
\begin{align*}
\omega=1 または \omega^2=1
\end{align*}
$$
となり矛盾します。何度も述べているように、$${\omega}$$ は「3乗して1になる数(1の3乗根)のうち複素数である定数」、具体的には
$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$ または $${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので、これは矛盾です (step3)。
(図解)
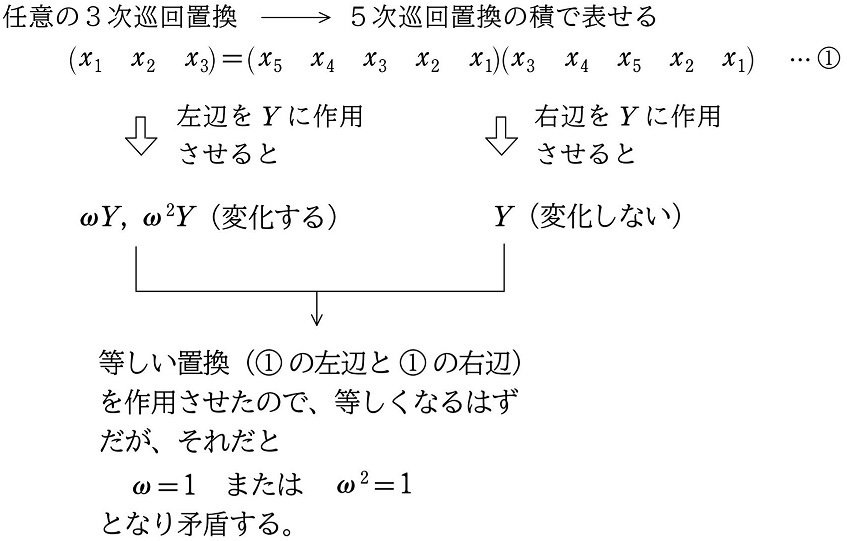
すると、矛盾が生じた理由は5次方方程式に解の公式が存在すると仮定したこと、詳しく言うと、5次方程式の解の公式を加減乗除 ($${\small +, -, \times, \div}$$) と累乗根 ($${\scriptsize \sqrt{ }, \sqrt[3]{ }, \cdots}$$) を用いて構成できると仮定したことにあります。つまり、この仮定が間違いであることが示されたので、背理法により5次方程式に解の公式が存在しないことが証明されました (step4)(注9)。
なお、2次方程式、3次方程式、4次方程式については、この議論は適用できません。本証明では、次の $${➀}$$ 式
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
が重要な役割を担いましたが、2次方程式は2つの解、3次方程式は3つの解、4次方程式は4つの解までしか持たないので、5次方程式の5つの解
$${x_1, x_2, x_3, x_4, x_5}$$
で構成される $${➀}$$ 式は、4次以下の方程式では構成できません。実際、4次方程式までには解の公式は存在します(注10)。
また6次方程式の場合は、6次方程式には6つの解
$${x_1, x_2, x_3, x_4, x_5, x_6}$$
があるので、その6つの解から任意に3つを選んで3次巡回置換を作ることができ、その3次巡回置換は5次巡回置換の積で表すことができるので、5次方程式のときと同様にして、$${➀}$$ を用いて解の公式が存在しないことが証明されます。つまり6次方程式においても、構成可能な式の拡大は差積の添加(平方根の添加)までで、それ以上は拡大できない(つまり、対称性の破壊は偶置換シンメトリーまでで、それ以上破壊できない)ということになります。
これは7次方程式、8次方程式 $${\cdots}$$ と次数が高くなっても同じことが言えるので、これによって、5次以上の方程式には解の公式が存在しないことが証明されました」
時計は午後8時を回り、家庭教師の終了時間はとうに過ぎていた。食欲を誘うカレーの香りが漂う。
竹村は自分の用意したノートを見た。あきらかに森田君のそれより、まとまっていない数式の羅列があった。
「そうか?」森田君が何かに気付いたような表情を見せた。
「先生、これ置換の構造だけに着目すればもっと厳密な証明ができそうです」
「どうゆうこと?」
「解の置換の構造です。今回は5次方程式の解の公式が存在すると仮定して、矛盾を導きだすために解の置換を利用しました。しかし解の置換の構造そのものを洞察すれば、もっと本質に迫った議論で解の公式が存在しないことが証明できそうです。先生、次の時間までにやってみます!」
家庭教師は終わり、竹村は馴染みの小料理屋に向かった。
「ママ、うちの生徒の森田君なんだけど、彼、ガロアが発明した群に気付いたのかな・・・」
「ガレットデロワ? 森田君、良いセンスしてるわね、ちょうどパイ生地とアーモンドクリームがあるので作ってみましょうか」
窓の外をみると5つの星があった。それらの星が一体となって、規則正しく複雑な動きでクルクルと回っているように竹村には見えた。
(了)
終わりに
本シリーズの証明はアーベルの証明そのものではなく、主に『不可能の証明』(津田文夫著)を参考に、アーベルの証明(アーベル・ルフィニの定理)のアイデア(解の置換や累乗根の添加など)が分かるように、なるべく簡潔に書いています。アーベルの証明そのものは、式変形を駆使したかなり複雑な証明になっており、非常に分かりにくい所もあります。
なお『群と代数方程式』(守屋美賀雄訳・解説)によれば、アーベルの証明について「現代代数学の立場からみれば、ここに訳出したアーベルの論文は記述上いろいろな点で不備が指摘できるであろう」(原文まま)ということのようです。古典的な数学が好きなので、機会があればアーベルの証明そのものの解説にも挑戦したいと思います。
このあとは、ガロアによる、いわゆる「群」を用いた証明へと内容は発展していきますが、この証明までやるかどうかは未定です。ガロアによる証明は、アーベルの証明とは違って書籍が沢山あります。
その代わりスピンオフとして、説明が難しかったと思われる「累乗根の添加」と「対称性の破壊」について、馴染みのある2次方程式を使って、もっと具体的で分かりやすい解説をする予定です。やや心残りがあるもう少しアーベルの証明にこだわってみます。
簡単な歴史的背景
5次以上の方程式に解の公式が存在しないことの証明は、最初にイタリアの数学者パオロ・ルフィニが、ラグランジュの考えた置換の理論を引き継いで『方程式の一般理論』(1799 年)という論文で提出しましたが、その内容に欠陥があり、その欠陥が解決された完全な形で証明したのがノルウェーの数学者ニールス・アーベルです。


アーベルはそのその証明を、以下の論文
『5次の一般方程式の解法の不可能性を証明する代数方程式についての論文』(1824年)
さらに詳細に書いた
『4次より高い次数の代数方程式を一般には解くことが不可能であることの証明』(1826年)
という論文で提出しています。なおアーベルは、地理的な問題もあり、大数学者ではなかったルフィニの論文は存在すら知らなかったようです。アーベルは1826年、パリに留学した際にルフィニの論文の存在を知り、その内容について根本的な性質の証明が足りない事に気付いたとのこと。一般にこの証明は、現在ではルフィニの貢献も考慮して『アーベル・ルフィニの定理』と呼んでいます。
なお、ルフィニの証明の欠陥については、『群の発見』(原田耕一郎著)(2001年)に詳しい。簡単には書けないので、ここでは割愛します。
アーベルの証明とガロアの証明の違い
アーベルの証明(アーベル・ルフィニの定理)とガロアの証明との違いは(ここは個人的な解釈が入るのですが)、アーベルの証明では、差積やラグランジュ・リゾルベントのような「適当な式」の添加によって解の公式が構成できるか、できないかに力点が置かれ、その添加する「適当な式」の属性として解の置換(対称性の破壊)が語られています。あくまでも「式」の方が主役です。
一方、ガロアの証明は解の置換(今の言葉で言う置換群)の構造そのものに着目して、「解の置換」がこういう構造になっていれば解の公式は存在する、逆に「解の置換」がこういう構造になっていなければ解の公式は存在しないと、「解の置換」そのものに力点が置かれています。具体的な数式ではなく、「解の置換」そのものが主役になっており、主役が逆転しているのです。
ガロアは、より抽象的な解の置換(置換群)の構造そのもに焦点を当てており、ガロアが群論の創始者と言われているのはそういう理由です。

(注1)『背理法』について(復習)
『背理法』とは、「ある命題の結論が正しいことを証明するために、その結論の否定を仮定して、すでに真であるとわかっている事実や元の命題の仮設などに矛盾することから、その命題の結論が正しいことを証明する方法」
例えば次の命題を背理法で証明しましょう。
命題『ある整数 $${n}$$ について $${n^2}$$ が偶数であるとする。このとき $${n}$$ は偶数である。』
(証明)
この命題の結論は「$${n}$$ は偶数である」。この結論の否定、つまり「$${n}$$ は奇数である」と仮定する(背理法の仮定)。$${n}$$ は奇数なので、$${k}$$ を $${0}$$ 以上の整数 ($${0, 1, 2, 3, \cdots}$$) として $${n=2k+1}$$ とおける *。
ここで展開公式
$${(a+b)^2=a^2+2ab+b^2}$$
を用いると
$$
\begin{align*}
n^2&=(2k+1)^2\\
&=(2k)^2+2\cdot2k\cdot1+1^2\\
&=4k^2+4k+1\\
&=2(2k^2+2k)+1\\
&=2l+1 (ただし l=2k^2+2k とおいた)
\end{align*}
$$
すると、$${k}$$ は $${0}$$ 以上の整数であることから、$${l(=2k^2+2k)}$$ も $${0}$$ 以上の整数となるので、 $${2l+1}$$ は奇数である*。これは $${n^2}$$ が偶数であるという条件(元の命題の仮設)に矛盾しているので、これによって背理法の仮定「$${n}$$ は奇数である」が正しくないこと、つまり「$${n}$$ は偶数である」ことが証明された。(証明終)
*奇数 $${1, 3, 5, 7, \cdots}$$ は
$${1=2\times0+1}$$
$${3=2\times1+1}$$
$${5=2\times2+1}$$
$${7=2\times3+1}$$
$${\hspace{23pt}\vdots}$$
より、$${n=2k+1}$$($${k}$$ は $${0}$$ 以上の整数)の形で書ける。
(注2)対称性を恒等置換にまで破壊する理由(復習)
解の公式を構成するにあたって、構成可能な式の対称性を、なぜ恒等置換まで破壊させる必要があるのか。その理由は、解の式 $${x_1, x_2, \cdots}$$ のすべてを変化せない置換は恒等置換のみだからです。例えば3次方程式の解 $${x_1, x_2, x_3}$$ に恒等置換を作用させても、$${x_1, x_2, x_3}$$ はいずれも変化しません。
$$
\begin{align*}
x_1 &x_2 x_3\\
&\downarrow {\small 恒等置換を作用}\\
x_1 &x_2 x_3 {\small \Leftarrow いずれも変化しない}
\end{align*}
$$
解の公式は文字通り解を表す式なので、解の式 $${x_1, x_2, \cdots}$$ と同等の対称性をもちます。解の公式を変化させない置換は恒等置換のみです。よって、次々と都合のいい式を添加していき、最終的に構成可能な式の対称性(式を変化させない置換)を恒等置換にまで破壊できれば、それまでに添加された式の加減乗除によって、はれて解の公式が実現できるわけです。
(注3)2次方程式に解の公式が存在すること(復習)
2次方程式では、我々が普通に使っている数と文字係数の加減乗除で表される式全体の集合 $${Q}$$ (これは対称式の集合になる)に、「条件Ⅰ」を満たす解の式 $${X}$$ として差積
$${X_2=\alpha-\beta}$$
を添加し、構成可能な式の集合を $${Q(X_2)}$$ に拡大することによって、2次方程式の解の公式が構成可能となりました(本シリーズ (11)、(13))。
$$
\begin{gather*}
\,\,Q\\
\hspace{67pt}\downarrow \Leftarrow X_2 の添加\\
Q(X_2)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf 2次置換(対称式)}\\
\hspace{67pt}\downarrow \Leftarrow X_2 の添加\\
{\bf 恒等置換}
\end{gather*}
$$
このとき、構成可能な式の対称性(式を変えない置換)が、2次置換(対称式)から恒等置換にまで破壊されていることに注意してください。構成可能な式が拡大すると、それに対応して対称性は縮小(破壊)されていきます。そして構成可能な式の対称性が、完全に対称性の破壊された恒等置換にまで辿り着いたとき、2次方程式の解の公式は構成可能となります。

上の内容をもう少し詳しく言うと、差積の2乗
$${(X_2)^2=(\alpha-\beta)^2}$$
は対称式なので、集合 $${Q}$$ 内で加減乗除によって構成可能となります(以下、構成可能というのは加減乗除で構成可能という意味)。
しかし、その平方根 $${\sqrt{(X_2)^2}}$$ は $${Q}$$ 内では構成可能ではないので、 $${Q}$$ に $${\sqrt{(X_2)^2}}$$ を添加して、構成可能な式の集合を $${Q(\sqrt{(X_2)^2})}$$ へと拡大します。なお
$${\sqrt{(X_2)^2}=X_2, -X_2}$$
より、$${\sqrt{(X_2)^2}}$$ を添加することと $${X_2}$$ を添加することは同じなので*、$${Q(\sqrt{(X_2)^2})}$$ と $${Q(X_2)}$$ は同じ集合となり
$${Q(\sqrt{(X_2)^2})=Q(X_2)}$$
この集合 $${Q(X_2)}$$ 内で構成可能なすべての式を、変化させない置換は恒等置換のみです。よってこの集合 $${Q(X_2)}$$ 内で、恒等置換と同等の対称性をもつ2次方程式の解の公式がはれて構成可能となります。
*$${\sqrt{(X_2)^2}}$$ を添加することと、単に $${X_2}$$ を添加することは同じになります。その理由は
$${\sqrt{(X_2)^2}=\underline{X_2}, -X_2}$$
より、$${\sqrt{(X_2)^2}}$$ は $${X_2}$$ そのものか、それに $${-1}$$ を掛けた $${-X_2}$$ です。 つまり、$${\sqrt{(X_2)^2}}$$ の添加によって自動的に $${X_2}$$(下線部)も添加されます。逆に $${X_2}$$ の添加によって、それに $${-1}$$ を掛ければ $${-X_2}$$ も合わせて構成できるので、 $${X_2}$$ を添加すれば $${\sqrt{(X_2)^2}}$$ を添加したことと同じになります。
$${\sqrt{(X_2)^2}}$$ の添加 $${\longrightarrow}$$ $${X_2}$$ の添加
$${X_2}$$ の添加 $${\longrightarrow}$$ $${-X_2}$$ は構成可能
$${\hspace{57pt}\longrightarrow}$$ $${\sqrt{(X_2)^2}}$$ の添加
すなわち
「$${\sqrt{(X_2)^2}}$$ を添加するのと $${X_2}$$ を添加するのは同じ」
こととなり、$${Q(\sqrt{(X_2)^2})}$$ と、$${\sqrt{(X_2)^2}}$$ の代わりに $${X_2}$$ を添加した $${Q(X_2)}$$ は同じ集合となります。
$${Q(\sqrt{(X_2)^2})=Q(X_2)}$$
(注4)3次方程式に解の公式が存在すること(復習)
3次方程式では、我々が普通に使っている数と、$${1}$$ の3乗根のうち複素数である定数 $${\omega}$$、及び文字係数の加減乗除で表される式全体の集合 $${Q(\omega)}$$ (これは対称式の集合になる)に、最初に「条件Ⅰ」を満たす解の式 $${X}$$ として差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を添加(これは平方根 $${\sqrt{X_5}}$$ を添加することと同じ)、次に「条件Ⅱ」を満たす解の式 $${Y}$$ としてラグランジュ・リゾルベント
$${A=\alpha+\beta\omega+\gamma\omega^2}$$
を添加し、構成可能な式の集合を $${Q(\omega, X_3, A)}$$ に拡大することによって、3次方程式の解の公式が構成可能となりました(本シリーズ (12)、(13))。
$$
\begin{gather*}
Q(\omega)\\
\hspace{67pt}\downarrow \Leftarrow X_3 の添加\\
Q(\omega, X_3)\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
Q(\omega, X_3, A)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf 3次置換(対称式)}\\
\hspace{67pt}\downarrow \Leftarrow X_3 の添加\\
{\bf 偶置換シンメトリー}\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
{\bf 恒等置換}
\end{gather*}
$$
このとき、構成可能な式の対称性(式を変えない置換)は、3次置換(対称式)、偶置換シンメトリー、恒等置換へと段階的に破壊されていきます。構成可能な式が拡大すると、それと対応して対称性は縮小(破壊)されていくわけです。そして2次方程式のときと同様に、構成可能な式の対称性が、完全に対称性の破壊された恒等置換にまで辿り着いたとき、3次方程式の解の公式は構成可能となります。


上の内容をもう少し詳しく言うと、差積の2乗
$${(X_3)^2={\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2}$$
は対称式なので、集合 $${Q(\omega)}$$ 内で加減乗除によって構成可能となります(以下、構成可能というのは加減乗除で構成可能という意味)。
しかし、その平方根 $${\sqrt{(X_3)^2}}$$ は $${Q(\omega)}$$ 内では構成可能ではないので、 $${Q(\omega)}$$ に $${\sqrt{(X_3)^2}}$$ を添加して、構成可能な式の集合を $${Q(\omega, \sqrt{(X_3)^2})}$$ へと拡大します。この集合 $${Q(\omega, \sqrt{(X_3)^2})}$$ 内で構成可能な式は、偶置換シンメトリーをもちます。なお
$${\sqrt{(X_3)^2}=X_3, -X_3}$$
より、$${\sqrt{(X_3)^2}}$$ を添加することと $${X_3}$$ を添加することは同じなので*、$${Q(\omega, \sqrt{(X_3)^2})}$$ と $${Q(\omega, X_3)}$$ は同じ集合となり
$${Q(\omega, \sqrt{(X_3)^2})=Q(\omega, X_3)}$$
ここまでは2次方程式のときと同じストーリーです。
しかし集合 $${Q(\omega, X_3)}$$ 内で3次方程式の解の公式は構成可能ではないので、次のステップとしてラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
を考えます。ラグランジュ・リゾルベントの3乗
$${A^3=(\alpha+\omega\beta+\omega^2\gamma)^3}$$
は偶置換シンメトリーをもつので、同じく偶置換シンメトリーをもつ集合 $${Q(\omega, X_3)}$$ 内で構成可能となります。しかし、その3乗根 $${\sqrt[3]{A^3}}$$ は $${Q(\omega, X_3)}$$ 内では構成可能ではないので、 $${Q(\omega, X_3)}$$ に $${\sqrt[3]{A^3}}$$ を添加して、構成可能な式の集合を $${Q(\omega, X_3, \sqrt[3]{A^3})}$$ へと拡大します。なお
$${\sqrt[3]{A^3}=A, \omega A, \omega^2A}$$
より、$${\sqrt[3]{A^3}}$$ を添加することと $${A}$$ を添加することは同じなので**、$${Q(\omega, X_3, \sqrt[3]{A^3})}$$ と $${Q(\omega, X_3, A)}$$ は同じ集合となり
$${Q(\omega, X_3, \sqrt[3]{A^3})=Q(\omega, X_3, A)}$$
この集合 $${Q(\omega, X_3, A_3)}$$ 内で構成可能なすべての式を、変化させない置換は恒等置換のみです。よってこの集合 $${Q(\omega, X_3, A_3)}$$ 内で、恒等置換と同等の対称性をもつ3次方程式の解の公式がはれて構成可能となります。
*$${\sqrt{(X_3)^2}}$$ を添加することと、単に $${X_3}$$ を添加することは同じになります。その理由は(注3)でやった $${X_2}$$ の場合と同じ論法です。
$${\sqrt{(X_3)^2}=\underline{X_3}, -X_3}$$
より、$${\sqrt{(X_3)^2}}$$ は $${X_3}$$ そのものか、それに $${-1}$$ を掛けた $${-X_3}$$ です。 つまり、$${\sqrt{(X_3)^2}}$$ の添加によって自動的に $${X_3}$$(下線部)も添加されます。逆に $${X_3}$$ の添加によって、それに $${-1}$$ を掛ければ $${-X_3}$$ も合わせて構成できるので、 $${X_3}$$ を添加すれば $${\sqrt{(X_3)^2}}$$ を添加したことと同じになります。
$${\sqrt{(X_3)^2}}$$ の添加 $${\longrightarrow}$$ $${X_3}$$ の添加
$${X_3}$$ の添加 $${\longrightarrow}$$ $${-X_3}$$ は構成可能
$${\hspace{57pt}\longrightarrow}$$ $${\sqrt{(X_3)^2}}$$ の添加
すなわち
「$${\sqrt{(X_3)^2}}$$ を添加するのと $${X_3}$$ を添加するのは同じ」
こととなり、$${Q(\omega, \sqrt{(X_3)^2})}$$ と、$${\sqrt{(X_3)^2}}$$ の代わりに $${X_3}$$ を添加した $${Q(\omega, X_3)}$$ は同じ集合となります。
$${Q(\omega, \sqrt{(X_3)^2})=Q(\omega, X_3)}$$
**$${\sqrt[3]{A^3}}$$ を添加することと、単に $${A}$$ を添加することは同じになります。その理由は
$${\sqrt[3]{{A}^3}=\underline{A}, \omega A, \omega^2A}$$
より、$${\sqrt[3]{{A}^3}}$$ は $${A}$$ そのものか、$${\omega}$$ を1回掛けた $${\omega A}$$ か、$${\omega}$$ を2回掛けた $${\omega^2A}$$ となります。集合 $${Q}$$ にはあらかじめ $${\omega}$$ が添加されているので、$${\omega}$$ は加減乗除の計算に自由に使えます。つまり、$${\sqrt[3]{{A}^3}}$$ の添加によって自動的に $${A}$$(下線部)も添加され、逆に $${A}$$ の添加によって、$${\omega A}$$ と $${\omega^2A}$$ も合わせて構成できるので、 $${A}$$ を添加すれば $${\sqrt[3]{{A}^3}}$$ を添加したことと同じになります。
$${\sqrt[3]{{A}^3}}$$ の添加 $${\longrightarrow}$$ $${A}$$ の添加
$${A}$$ の添加 $${\longrightarrow}$$ $${\omega A}$$ と $${\omega^2A}$$ は構成可能
$${\hspace{53pt}\longrightarrow}$$ $${\sqrt[3]{{A}^3}}$$ の添加
すなわち
「$${\sqrt[3]{{A}^3}}$$ を添加するのと $${A}$$ を添加するのは同じ」
こととなり、$${Q(\omega, X_3, \sqrt[3]{{A}^3})}$$ と、$${\sqrt[3]{{A}^3}}$$ の代わりに $${A}$$ を添加した $${Q(\omega, X_3, A)}$$ は同じ集合となります。
$${Q(\omega, X_3, \sqrt[3]{A^3})=Q(\omega, X_3, A)}$$
(注5)差積の2乗の平方根を添加することと、単に差積を添加することは同じであること(復習)
$${\sqrt{(X_5)^2}}$$ を添加することと、単に $${X_5}$$ を添加することは同じになります。その理由は(注3)でやった $${X_2}$$ や、(注4)でやった $${X_3}$$ と同じ論法です。
$${\sqrt{(X_5)^2}=\underline{X_5}, -X_5}$$
より、$${\sqrt{(X_5)^2}}$$ は $${X_5}$$ そのものか、それに $${-1}$$ を掛けた $${-X_5}$$ です。 つまり、$${\sqrt{(X_5)^2}}$$ の添加によって自動的に $${X_5}$$(下線部)も添加されます。逆に $${X_5}$$ の添加によって、それに $${-1}$$ を掛ければ $${-X_5}$$ も合わせて構成できるので、 $${X_5}$$ を添加すれば $${\sqrt{(X_5)^2}}$$ を添加したことと同じになります。
$${\sqrt{(X_5)^2}}$$ の添加 $${\longrightarrow}$$ $${X_5}$$ の添加
$${X_5}$$ の添加 $${\longrightarrow}$$ $${-X_5}$$ は構成可能
$${\hspace{57pt}\longrightarrow}$$ $${\sqrt{(X_5)^2}}$$ の添加
すなわち
「$${\sqrt{(X_5)^2}}$$ を添加するのと $${X_5}$$ を添加するのは同じ」
こととなり、$${Q(\omega, \sqrt{(X_5)^2})}$$ と、$${\sqrt{(X_5)^2}}$$ の代わりに $${X_5}$$ を添加した $${Q(\omega, X_5)}$$ は同じ集合となります。
$${Q(\omega, \sqrt{(X_5)^2})=Q(\omega, X_5)}$$
(注6)置換の積の順番について(復習)
大学の教科書では、置換は右から(後ろから)作用させると決められていますが、本シリーズではわかりやすさを優先して、左から(前から)作用させると定義しています。
$$
\begin{align*}
(x_1 x_2 x_3)=\underset{先に作用}{(x_5 x_4 x_3 x_2 x_1)}\underset{後に作用}{(x_1 x_3 x_4 x_5 x_2)} \cdots ①
\end{align*}
$$
(注7)すべての3次巡回置換を5次巡回置換の積で表す
5つの解で構成できる3次巡回置換は全部で15通りありますが、それらをすべて5次巡回置換の積で表すと以下のようになります。本文で述べた「任意の3次巡回置換を5次巡回置換の積で表す一般的な構成方法」の (step1~4) に従って、容易に構成することができます。
$$
\begin{align*}
&(x_1 〇 〇) 型\\
&① (x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1)\\
&② (x_1 x_2 x_4)=(x_5 x_3 x_4 x_2 x_1)(x_4 x_3 x_5 x_2 x_1)\\
&③ (x_1 x_2 x_5)=(x_4 x_3 x_5 x_2 x_1)(x_5 x_3 x_4 x_2 x_1)\\
&④ (x_1 x_3 x_2)=(x_5 x_4 x_2 x_3 x_1)(x_2 x_3 x_4 x_3 x_1)\\
&⑤ (x_1 x_3 x_4)=(x_5 x_2 x_4 x_3 x_1)(x_4 x_2 x_5 x_3 x_1)\\
&⑥ (x_1 x_3 x_5)=(x_4 x_2 x_5 x_3 x_1)(x_5 x_2 x_4 x_3 x_1)\\
&⑦ (x_1 x_4 x_2)=(x_5 x_3 x_2 x_4 x_1)(x_2 x_3 x_5 x_4 x_1)\\
&⑧ (x_1 x_4 x_3)=(x_5 x_2 x_3 x_4 x_1)(x_3 x_2 x_5 x_4 x_1)\\
&⑨ (x_1 x_4 x_5)=(x_3 x_2 x_5 x_4 x_1)(x_5 x_2 x_3 x_4 x_1)\\
&⑩ (x_1 x_5 x_2)=(x_4 x_3 x_2 x_5 x_1)(x_2 x_3 x_4 x_5 x_1)\\
&⑪ (x_1 x_5 x_3)=(x_4 x_2 x_3 x_5 x_1)(x_3 x_2 x_4 x_5 x_1)\\
&⑫ (x_1 x_5 x_4)=(x_3 x_2 x_4 x_5 x_1)(x_4 x_2 x_3 x_5 x_1)\\[5pt]
&(x_2 〇 〇) 型\\
&⑬ (x_2 x_3 x_4)=(x_5 x_1 x_4 x_3 x_2)(x_4 x_1 x_5 x_3 x_2)\\
&⑭ (x_2 x_3 x_5)=(x_4 x_1 x_5 x_3 x_2)(x_5 x_1 x_4 x_3 x_2)\\
&⑮ (x_2 x_4 x_3)=(x_5 x_1 x_3 x_4 x_2)(x_3 x_1 x_5 x_4 x_2)\\
&⑯ (x_2 x_4 x_5)=(x_3 x_1 x_5 x_4 x_2)(x_5 x_1 x_3 x_4 x_2)\\
&⑰ (x_2 x_5 x_3)=(x_4 x_1 x_3 x_5 x_2)(x_3 x_1 x_4 x_5 x_2)\\
&⑱ (x_2 x_5 x_4)=(x_3 x_1 x_4 x_5 x_2)(x_4 x_1 x_3 x_5 x_2)\\[5pt]
&(x_3 〇 〇) 型\\
&⑲ (x_3 x_4 x_5)=(x_2 x_1 x_5 x_4 x_3)(x_5 x_1 x_2 x_4 x_3)\\
&⑳ (x_3 x_5 x_4)=(x_2 x_1 x_4 x_5 x_3)(x_4 x_1 x_2 x_5 x_3)
\end{align*}
$$
(注8)Y≠0 となる理由
次の「条件Ⅱ」
「条件Ⅱ」
『$${Y}$$ はある偶置換(3次巡回置換)で変化するが、$${Y^3}$$ はすべての偶置換(3次巡回置換)で変化しない(ただし $${Y^3}$$ は対称式ではない)』
より、$${Y=0}$$ となることはありえません。なぜなら、 仮に $${Y=0}$$ とすると「条件Ⅱ」の前半の条件
『$${Y}$$ はある偶置換(3次巡回置換)で変化する』
より、$${Y=0}$$ を変化させる偶置換(3次巡回置換)は少なくとも1つ存在する必要がありますが、そのような偶置換(3次巡回置換)は存在しないからです。どのような偶置換(3次巡回置換)を $${0}$$ に作用させても、$${0}$$ は $${0}$$ のままで変化しません。
$$
\begin{align*}
&\,\,0\\
{\small 偶置換(3次巡回置換) \rightarrow} &\Downarrow\\
&\,\,0 {\small \leftarrow 変化しない}
\end{align*}
$$
以上より $${Y\ne0}$$ となり、同時に$${Y^3\ne0}$$ も示されます。
(注9)より厳密には・・・
これにより「5次方程式には解の公式が存在しない」と結論するには、これまでやってきたように(思いっ切り平たく言えば)
『解の公式があるとすれば、係数の加減乗除で表せる集合に、平方根、3乗根と次々と累乗根を添加し(及び、必要に応じて $${\omega}$$ のような1の累乗根のうち複素数である定数を添加し)、構成可能な式を段階的に拡大(それに対応して、構成可能な式の対称性を段階的に破壊)させることによって、どこかの段階で解の公式が構成可能になる』$${\cdots (*)}$$
という命題を初めに明示し、その証明をきちんと与える必要があります。
しかし本シリーズでは、5次方程式には解の公式が存在しないアーベルの証明(アーベル・ルフィニの定理)のもっとも素朴な部分のアイデア(解の置換や累乗根の添加など)を、手早く紹介したいということで割愛しました。
なお、この $${(*)}$$ の証明は、『不可能の証明』(津田文夫著)に詳しく紹介されています。必要があれば別の機会(補足として章末に上げる?)にしたいと思います。
(注10)4次巡回置換についての注意事項
なお、4次置換においても $${①}$$ 式
$$
\begin{align*}
(x_1 x_2 x_3)=(x_5 x_4 x_3 x_2 x_1)(x_3 x_4 x_5 x_2 x_1) \cdots ①
\end{align*}
$$
のような式を構成することができます。次のような「任意の3次巡回置換は4次巡回置換の積で表すことができる」という関係式です。
$$
\begin{align*}
(x_1 x_2 x_3)=(x_4 x_3 x_2 x_1)(x_3 x_4 x_2 x_1) \cdots ⑮
\end{align*}
$$
この関係式が正しいことを、4次方程式の解の列 $${x_1 x_2 x_3 x_4}$$ に作用させて確認します。
(左辺)$${=(x_1 x_2 x_3)}$$ を作用させると
$$
\begin{align*}
x_1 x_2& x_3 x_4\\
&\Downarrow (x_1 x_2 x_3) を作用\\
x_2 x_3& x_1 x_4 (*5)
\end{align*}
$$
(右辺)$${=(x_4 x_3 x_2 x_1)(x_1 x_3 x_4 x_2)}$$
作用させると、左から(前から)順に作用させて
$$
\begin{align*}
x_1 x_2& x_3 \underline{x_4}\\
&\Downarrow (x_4 x_3 x_2 x_1) を作用\\
x_4 x_1& x_2 x_3\\
&\Downarrow (x_3 x_4 x_2 x_1) を作用\\
x_2 x_3& x_1 \underline{x_4} (*6)
\end{align*}
$$
よって、$${(*5)}$$ と $${(*6)}$$ は同じ結果となり $${⑮}$$ は成り立ちます。4次巡回置換を作用させても $${x_4}$$ は変化せず(下線部)、$${(x_1, x_2, x_3)}$$ の巡回置換だけが残ることがポイントです。
この式を用いれば、同じ議論で4次方程式の解の公式が存在しないことが証明できそうですが、4次巡回置換は奇数個の互換の積で表せるので奇置換です。
(例)
$$
\begin{align*}
\underset{\footnotesize 4次巡回置換}{\underline{(x_1 x_2 x_3 x_4)}}=\underset{\footnotesize 奇数個(3個)の互換の積}{\underline{(x_1 x_2)(x_1 x_3)(x_1 x_4)}}
\end{align*}
$$
つまり、任意の3次巡回置換は「奇置換」である4次巡回置換の積で表せたことになります。
$$
\begin{align*}
\underset{偶置換}{\underline{(x_1 x_2 x_3)}}
=\underset{奇置換}{\underline{(x_4 x_3 x_2 x_1)}}\,
\underset{奇置換}{\underline{(x_3 x_4 x_2 x_1)}} \cdots ⑮
\end{align*}
$$
一方、5次巡回置換は「偶置換」でした。
$$
\begin{align*}
\underset{偶置換}{\underline{(x_1 x_2 x_3)}}
=\underset{偶置換}{\underline{(x_5 x_4 x_3 x_2 x_1)}}\,
\underset{偶置換}{\underline{(x_3 x_4 x_5 x_2 x_1)}} \cdots ①
\end{align*}
$$
偶置換である3次巡回置換は、同じく「偶置換」である5次巡回置換の積で表せることによって矛盾($${\omega=1}$$ または $${\omega^2=1}$$)が引き起こされました。
一方、4次巡回置換は「奇置換」であるため、$${⑮}$$ のように3次巡回置換を4次巡回置換の積で表せたとしても、5次方程式のときと同様の議論は適用できません。5次”以上”の方程式において、$${①}$$ を用いて解の公式が存在しないことが証明されます。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベント」による「3次方程式の解の公式」の導出
(8)「偶置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となることを解説
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「偶置換」にまで絞り込む(破壊する)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(破壊する)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から偶置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、偶置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての偶置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
いいなと思ったら応援しよう!

