
(追記あり)中学でも分かる①「微分法」
ここでは微分法の基本である
・極限
・微分係数
・導関数
を解説し、その応用として
・高次導関数
・偏微分
と内容を進めていきます。
目標は「接線の傾き」を求める
下図のように、グラフ上の点Aと接する直線ATを点Aにおける接線といい、その接する点Aを接点といいます。

ここでの目標は、その接線ATの傾きを求めることです。イングランドの数学者・物理学者、アイザック・ニュートンの発明した微分法です。高校の微分積分で習います。

そのために、グラフ上に別の点Bを用意し、2点A、Bを通る直線ABの傾きを求めます。こちらは中学数学の知識で求めることができます。

この直線ABの傾きから、微分法によって接線ATの傾きを求めます。
その前に、$${y=f(x)}$$ という関数の表記に慣れておきましょう。
y=f(x) という表記法
一般の関数 $${y=f(x)}$$ を考えます。なお、$${x}$$ の範囲は実数(つまり数直線上のすべての数)とします(参考1で数の分類)。

$${x}$$ の値が決まると、$${y=f(x)}$$ という関数によって $${y}$$ の値がただ1つに決まります。これが関数の定義です。
$$
\begin{align*}
x が決まる \xrightarrow[]{ y=f(x) } y の値がただ1つに決まる
\end{align*}
$$
例えは、関数 $${f}$$ として $${f(x)=x^2}$$ という関数を考えると
$${y=f(x)=x^2}$$
より
$${x=1}$$ のとき $${y=f(1)=1^2=1}$$
$${x=2}$$ のとき $${y=f(2)=2^2=4}$$
$${x=-3}$$ のとき $${y=f(-3)=(-3)^2=9}$$
$${x=\dfrac{9}{2}}$$ のとき $${y=f\left(\dfrac{9}{2}\right)={\left(\dfrac{9}{2}\right)}^2=\dfrac{81}{4}}$$
$${x=\sqrt{3}}$$ のとき $${y=f(\sqrt{3})={(\sqrt{3})}^2=3}$$
$${\hspace{23pt}\vdots}$$
と、実数 $${x}$$ を与えれば、関数 $${f(x)}$$ によって $${y}$$ の値がただ一つに決まります。$${x}$$ の範囲は実数なので、整数
$${\cdots, -2, -1, 0, 1, 2, \cdots}$$
の他に、有理数 $${\dfrac{9}{2}}$$ や無理数 $${\sqrt{3}}$$ でも上のように計算可能です。
y=f(x) のグラフ
関数 $${y=f(x)}$$ の $${x}$$ と $${y}$$ の関係を座標で表すことによって、$${y=f(x)}$$ のグラフを描くことができます。
例えば $${f(x)=2x}$$ とすると、それは
$${y=2x}$$
という1次関数になり、そのグラフは次のような直線になります。

下のようないくつかの点を $${xy}$$ 座標で結ぶことによって、原点Oを通る傾き $${2}$$ の直線になることが確認できます。
$${x=2}$$ のとき
$${y=f(2)=2\cdot2=4}$$ より P$${\hspace{-3pt}(2, 4)}$$
$${x=1}$$ のとき
$${y=f(1)=2\cdot1=2}$$ より Q$${\hspace{-3pt}(1, 2)}$$
$${x=0}$$ のとき
$${y=f(0)=2\cdot0=0}$$ より R$${\hspace{-3pt}(0, 0)}$$
$${x=-1}$$ のとき
$${y=f(-1)=2\cdot(-1)=-2}$$ より S$${\hspace{-3pt}(-1, -2)}$$
$${x=-2}$$ のとき
$${y=f(-2)=2\cdot(-2)=-4}$$ より T$${\hspace{-3pt}(-2, -4)}$$
なお、"$${\cdot}$$" はかけ算 "$${\times}$$" の意味です。今後この表記を頻繁に使います。
また、$${f(x)=x^2}$$ とすると、それは
$${y=x^2}$$
という2次関数になり、そのグラフは次のような放物線になります。
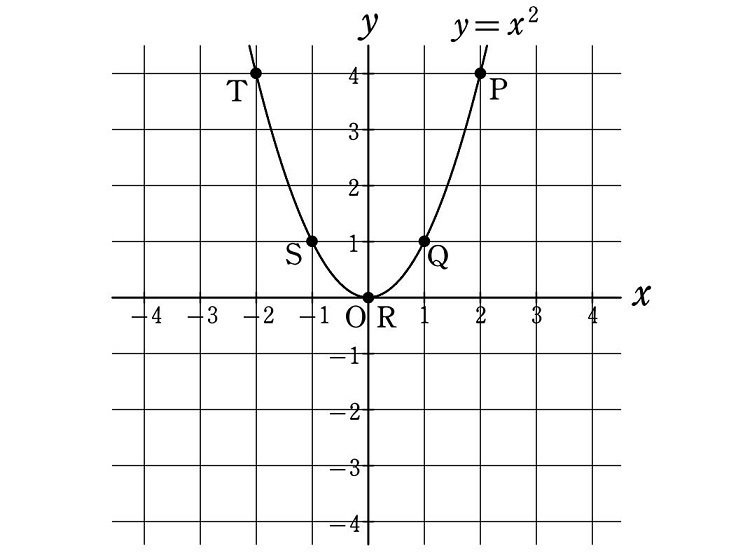
下のようないくつかの点を $${xy}$$ 座標でなめらかに結ぶことによって、原点Oを頂点とする放物線になることが確認できます。
$${x=2}$$ のとき
$${y=f(2)=2^2=4}$$ より P$${\hspace{-3pt}(2, 4)}$$
$${x=1}$$ のとき
$${y=f(1)=1^2=1}$$ より Q$${\hspace{-3pt}(1, 1)}$$
$${x=0}$$ のとき
$${y=f(0)=0^2=0}$$ より R$${\hspace{-3pt}(0, 0)}$$
$${x=-1}$$ のとき
$${y=f(-1)={(-1)}^2=1}$$ より S$${\hspace{-3pt}(-1, 1)}$$
$${x=-2}$$ のとき
$${y=f(-2)={(-2)}^2=4}$$ より T$${\hspace{-3pt}(-2, 4)}$$
ここからは具体的な $${f(x)}$$ は考えず、一般の関数 $${f(x)}$$ で話を進めていきます。後に、一般の場合で得た結論を、具体的な場合に適用していきます。
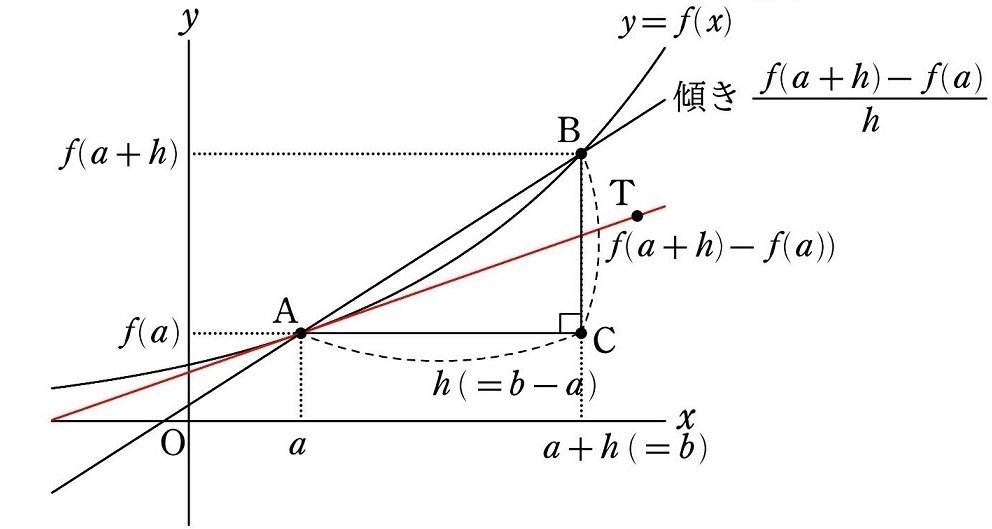
それでは、$${y=f(x)}$$ のグラフと、そのグラフ上の点AとBが下図のよう描かれたとして、直線ABの傾きを求めましょう。

直線ABの傾きを求める
上図の点Aの $${x}$$ 座標を $${a}$$ としたとき、点Aの $${y}$$ 座標は $${f(a)}$$ と表せるので、点Aの座標は A$${\hspace{-3pt}(a, f(a))}$$ となります。
$$
\begin{align*}
x=a \xrightarrow[]{ y=f(x) } y=f(a) \Rightarrow A\hspace{-1pt}(a, f(a))
\end{align*}
$$
同様に、上図の点Bの $${x}$$ 座標を $${b}$$ としたとき、点Bの $${y}$$ 座標は $${f(b)}$$ と表せるので、点Bの座標は B$${\hspace{-3pt}(b, f(b))}$$ となります。
$$
\begin{align*}
x=b \xrightarrow[]{ y=f(x) } y=f(b) \Rightarrow B\hspace{-1pt}(b, f(b))
\end{align*}
$$
図にすると下図のようになります。

すると、下図のように点Cを打つことによって

直線ABの傾きは
$$
\begin{align*}
\\[-12pt]
直線ABの傾き&=\dfrac{y の増加量}{x の増加量}\\[10pt]
&=\dfrac{線分BCの長さ}{線分ACの長さ}
\end{align*}
$$
で計算できます。この図より
線分ACの長さ $${=b-a}$$
線分BCの長さ $${=f(b)-f(a)}$$
なので、直線ABの傾きは
$$
\begin{align*}
\\[-12pt]
直線 AB の傾き&=\dfrac{線分BCの長さ}{線分ACの長さ}\\[10pt]
&=\dfrac{f(b)-f(a)}{b-a} \cdots (*1)
\end{align*}
$$

この $${(*1)}$$ は、中学では変化の割合、高校では平均変化率という用語で習います。
ここで、この式を変形していきます。まず
$$
\begin{align*}
b-a=h\\
\end{align*}
$$
と置きます。つまり、線分ACの長さを $${h}$$ とします。

$${a}$$ を移項すると
$$
\begin{align*}
b=a+h\\
\end{align*}
$$
これを、$${(*1)}$$ の $${a}$$ に代入($${a}$$ を消去)すると
$$
\begin{align*}
\dfrac{f(b)-f(a)}{b-a}=\dfrac{f(a+h)-f(a)}{h} \cdots (*2)
\end{align*}
$$
この $${b=a+h}$$ により、点Bの座標は
B$${\hspace{-3pt}(b, f(b))=}$$B$${\hspace{-3pt}(a+h, f(a+b))}$$
となり、2点 A$${\hspace{-3pt}(a, f(a))}$$、B$${\hspace{-3pt}(a+h, f(a+b))}$$ を通る直線ABの傾きは $${(*2)}$$ 式
$$
\begin{align*}
\dfrac{f(a+h)-f(a)}{h} \cdots (*2)
\end{align*}
$$
と表せます。$${h}$$ を用いて直線ABの傾きを表すことができました。

次に、この $${(*2)}$$ を用いて、点Aにおける接線AT(赤線)の傾きを求めます。

そのためには、新たに「極限」という概念を用います。
極限について
例えば、関数 $${f(x)=x^2}$$ において、$${x}$$ が $${2}$$ と異なる値をとりながら $${2}$$ に限りなく近づくとき、$${f(x)}$$ の値は
$${f(2)=2^2=4}$$
という値に限りなく近づきます。
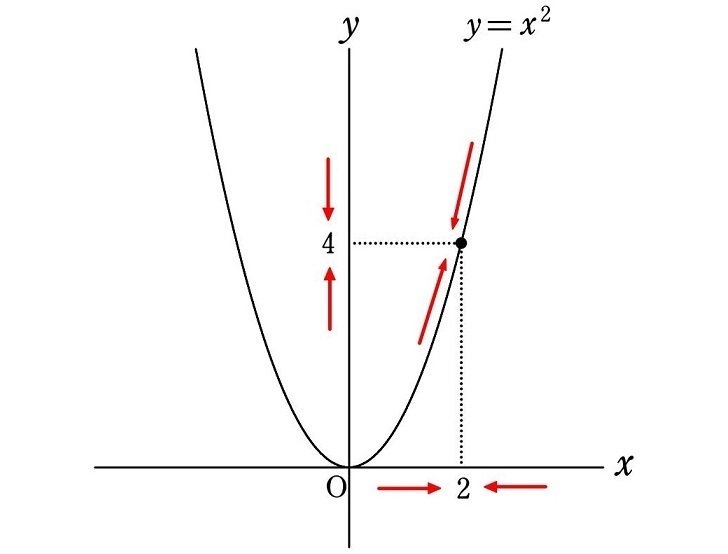
一般に、関数 $${f(x)}$$ において、$${x}$$ が $${a}$$ と異なる値をとりながら $${a}$$ に限りなく近づくとき、それに応じて $${f(x)}$$ のとる値が一定の値 $${A}$$ に限りなく近づくならば、この $${A}$$ を極限値といい、記号 $${\lim}$$ を用いて次のように表します。
$$
\begin{align*}
\lim_{x\rightarrow a}f(x)=A
\end{align*}
$$

***
$${\lim}$$ は ”リミット” と読み、$${x\hspace{-1pt}\rightarrow\hspace{-1pt}a}$$ は $${x}$$ を $${a}$$ に近づけることを意味しています。
(例)
$${\underset{x\rightarrow 2}{\lim}\,x^2=2^2=4}$$
$${\underset{x\rightarrow 0}{\lim}\,x^2=0^2=0}$$
$${\underset{x\rightarrow 3}{\lim}(x^3-1)=3^3-1=27-1=26}$$
$${a}$$ を定数とするとき
$${\underset{x\rightarrow 0}{\lim}(x+a)=0+a=a}$$
簡単な場合は、上記の(例)のように、近づける $${x}$$ の値をそのまま $${x}$$ に代入すれば極限値は求まります。本記事ではこのような簡単なケースのみを扱います(分母が $${0}$$ になるなど、そのまま代入できないケースは、高校3年の数学Ⅲの微分積分で習います)。
さて、接線の傾きを求めるには、直線ABの傾き
$$
\begin{align*}
\dfrac{f(a+h)-f(a)}{h} \cdots (*2)
\end{align*}
$$
に、この極限の考えを適用させます。
接線の傾きを求める方法
$${(*2)}$$ 式
$$
\begin{align*}
\dfrac{f(a+h)-f(a)}{h} \cdots (*2)
\end{align*}
$$
は直線ABの傾きです。今から求めるのは、点Aにおける接線AT(赤線)の傾きです。
それには、先ほどの $${(*2)}$$ について、「$${h}$$ を $${0}$$ に限りなく近づけていく」という方法をとります。先ほど解説した極限の考えです。
まずは準備として、点Aを定点(動かない点)、点Bを動点(動く点)とします。点Aはグラフ上に固定された点、点Bはグラフ上を動く点です。
ここで、$${h}$$ を $${0}$$ に限りなく近づけていくと、$${a+h (=b)}$$ は $${a}$$ に限りなく近づいていきます。つまり
$$
\begin{align*}
\lim_{h\rightarrow 0}(a+h)&=a+0(h=0 を代入)\\
&=a
\end{align*}
$$
すると、それに対応して、動点Bは定点Aに限りなく近づいていきます。

点Aは定点で、点Bが動く点なので、BがAに近づいていくことに注意します。
さらに、動点Bが定点Aに限りなく近づいていくと、直線ABは接線AT(赤線)に限りになく近づいていくことが見て取れます。

つまり、先ほどの直線ABの傾き
$$
\begin{align*}
\dfrac{f(a+h)-f(a)}{h} \cdots (*2)
\end{align*}
$$
について、$${h}$$ を $${0}$$ に限りなく近づけることによって、$${(*2)}$$ が限りなく一定の値に近づくならば、その近づく値(極限値)が点Aにおける接戦の傾きとなります。
それを、極限の記号 $${\lim}$$ を用いると、接線 ATの傾きは
$$
\begin{align*}
\lim_{h\rightarrow0}\dfrac{f(a+h)-f(a)}{h} \cdots (*3)
\end{align*}
$$
となります。$${h\hspace{-1pt}\rightarrow\hspace{-1pt}0}$$ のときの極限値が点Aにおける接戦の傾きです。
この $${(*3)}$$ について、改めてきちんとした定義を与えます。
微分係数の定義
関数 $${f(x)}$$ が定義されている(つまり $${f(x)}$$ が計算できる)区間の $${x}$$ の値 $${a}$$ に対して
$$
\begin{align*}
\lim_{h\rightarrow0}\dfrac{f(a+h)-f(a)}{h} \cdots (*3)
\end{align*}
$$
の極限値が存在するならば、これを $${f(x)}$$ の $${x=a}$$ における微分係数といい、$${f'(a)}$$ と表します。つまり
$$
\begin{align*}
f'(a)=\lim_{h\rightarrow0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}
$$
このとき、$${f(x)}$$ は $${x=a}$$ において微分可能であるといいます。
***
この $${f'(a)}$$ は、”$${f}$$ ダッシュ $${a}$$” や ”$${f}$$ プライム $${a}$$” と読みます。高校ではダッシュ、大学ではプライムが多く使われるようです。
微分係数の図形的意味
一般に、曲線上に定点Aと動点Bがあって、Bが曲線上を移動しながらAに限りなく近づくとき、直線ABが一定の直線ATに限りなく近づくならば、直線ATを点Aにおける曲線の接線といい、Aをこの接線の接点といいます。
したがって、$${x=a}$$ における関数 $${f(x)}$$ の微分係数
$$
\begin{align*}
f'(a)=\lim_{h\rightarrow0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}
$$
は、$${y=f(x)}$$ のグラフ上の点 A$${\hspace{-3pt}(a, f(a))}$$ における接線の傾きを表します。

***
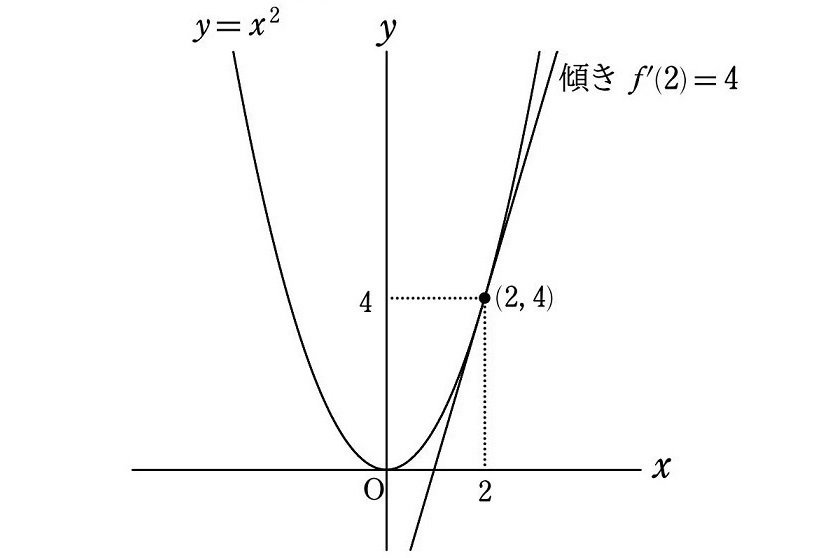
微分係数の具体例
例えば、$${f(x)=x^2}$$ として、そのときの $${x=2}$$ における微分係数 $${f'(2)}$$ を計算してみます。
中学で習う展開公式
$${(a+b)^2=a^2+2ab+b^2}$$
を用いて
$$
\begin{align*}
f(2+h)&=(2+h)^2\\
&=2^2+2\cdot2\cdot h+h^2\\
&=4+4h+h^2\\
f(2)&=2^2\\
&=4
\end{align*}
$$
より
$$
\begin{align*}
f'(2)&=\lim_{h\rightarrow0}\dfrac{f(2+h)-f(2)}{h}\\
&=\lim_{h\rightarrow0}\dfrac{\cancel{4}+4h+h^2-\cancel{4}}{h}\\
&=\lim_{h\rightarrow0}\dfrac{4h+h^2}{h}\\
&=\lim_{h\rightarrow0}\dfrac{(4+h)\cancel{h}}{\cancel{h}}\\
&=\lim_{h\rightarrow0}(4+h)\\
&=4+0(h=0 を代入)\\
&=4
\end{align*}
$$
よって、$${f(x)=x^2}$$ の $${x=2}$$ における微分係数は
$$
\begin{align*}
f'(2)=4
\end{align*}
$$
となります。そしてそれが、グラフ $${y=x^2}$$ 上の点 $${(2, f(2))=(2, 4)}$$ における接線の傾きになります。
導関数の定義
先ほどの微分係数
$$
\begin{align*}
f'(a)=\lim_{h\rightarrow0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}
$$
について、次のように、すべての $${a}$$ を $${x}$$ に置き換えた関数 $${f'(x)}$$ を導関数といいます。
$$
\begin{align*}
f'(x)=\lim_{h\rightarrow0}\dfrac{f(x+h)-f(x)}{h}
\end{align*}
$$

***
関数 $${f(x)}$$ から導関数 $${f'(x)}$$ を求めることを、$${f(x)}$$ を微分するといいます。肩に付いている記号 ”$${'}$$” は微分するという記号です。
この $${f'(x)}$$ は、”$${f}$$ ダッシュ $${x}$$” や ”$${f}$$ プライム $${x}$$” と読みます。$${f'(a)}$$ のときと同様に、高校ではダッシュ、大学ではプライムが多く使われるようです。
微分係数 $${f'(a)}$$ は具体的な値ですが、$${f'(x)}$$ は $${x}$$ の関数となります。$${x}$$ を決めることで $${f'(x)}$$ の具体的な値が決まります。
$$
\begin{align*}
x=a \xrightarrow[]{ f'(x) } f'(a) と決まる
\end{align*}
$$
(追記)
そして $${f'(x)}$$ は、グラフ $${y=f(x)}$$ 上の点 $${(x, f(x))}$$ における接線の傾きを表します。

導関数の具体例
それでは、いくつかの簡単な関数について、その導関数を求めてみます。
(例1)$${f(x)=x}$$ の導関数を求める。
$$
\begin{align*}
f(x+h)=x+h
\end{align*}
$$
より
$$
\begin{align*}
f'(x)&=\lim_{h\rightarrow0}\dfrac{f(x+h)-f(x)}{h}\\
&=\lim_{h\rightarrow0}\dfrac{\cancel{x}+h-\cancel{x}}{h}\\
&=\lim_{h\rightarrow0}\dfrac{\cancel{h}}{\cancel{h}}\\
&=\lim_{h\rightarrow0}1
\end{align*}
$$
この場合、$${h}$$ に関係なく定数 $${1}$$ と定まっているので
$$
\begin{align*}
f'(x)&=\lim_{h\rightarrow0}1\\
&=1
\end{align*}
$$
よって、$${f(x)=x}$$ の導関数は
$$
\begin{align*}
f'(x)=1
\end{align*}
$$
これを
$$
\begin{align*}
(x)'=1
\end{align*}
$$
と表すこともあります。これは、直線 $${y=x}$$ の傾きと同じになります。

(例2)$${f(x)=x^2}$$ の導関数を求める。
中学で習う2乗の展開公式
$${(a+b)^2=a^2+2ab+b^2}$$
を用いて
$$
\begin{align*}
f(x+h)&=(x+h)^2\\
&=x^2+2xh+h^2\\
\end{align*}
$$
より
$$
\begin{align*}
f'(x)&=\lim_{h\rightarrow0}\dfrac{f(x+h)-f(x)}{h}\\
&=\lim_{h\rightarrow0}\dfrac{\cancel{x^2}+2xh+h^2-\cancel{x^2}}{h}\\
&=\lim_{h\rightarrow0}\dfrac{2xh+h^2}{h}\\
&=\lim_{h\rightarrow0}\dfrac{(2x+h)\cancel{h}}{\cancel{h}}\\
&=\lim_{h\rightarrow0}(2x+h)\\
&=2x+0(h=0 を代入)\\
&=2x
\end{align*}
$$
よって、$${f(x)=x^2}$$ の導関数は
$$
\begin{align*}
f'(x)=2x
\end{align*}
$$
これを
$$
\begin{align*}
(x^2)'=2x
\end{align*}
$$
と表すこともあります。
この $${f'(x)=2x}$$ に $${x=1, 2, 3}$$ を代入してみると
$${f'(1)=2\cdot1=2}$$
$${f'(2)=2\cdot2=4}$$
$${f'(3)=2\cdot3=6}$$
と、順に大きくなることが分かります。
このことから、$${x}$$ が大きくなるにつれて、放物線 $${y=x^2}$$ に接する接線の傾きは大きくなることが見て取れます。

このように、導関数を調べることによって、接線の傾きの動向、ひいては曲線の曲がり具合(どんな感じでグラフが増減しているか)を知ることができます。
(例3)$${f(x)=x^3}$$ の導関数を求める。
高校で習う3乗の展開公式
$${(a+b)^3=a^3+3a^2b+3ab^2+b^3}$$
を用いて
$$
\begin{align*}
f(x+h)&=(x+h)^3\\
&=x^3+3x^2h+3xh^2+h^3
\end{align*}
$$
より
$$
\begin{align*}
f'(x)&=\lim_{h \rightarrow 0}\dfrac{f(x+h)-f(x)}{h}\\
&=\lim_{h \rightarrow 0}\dfrac{\cancel{x^3}+3x^2h+3xh^2+h^3-\cancel{x^3}}{h}\\
&=\lim_{h \rightarrow 0}\dfrac{3x^2h+3xh^2+h^3}{h}\\
&=\lim_{h \rightarrow 0}\dfrac{(3x^2+3xh+h^2)\cancel{h}}{\cancel{h}}\\
&=\lim_{h \rightarrow 0}(3x^2+3xh+h^2)\\
&=3x^2+3x\cdot0+0^2(h=0 を代入)\\
&=3x^2
\end{align*}
$$
よって、$${f(x)=x^3}$$ の導関数は
$$
\begin{align*}
f'(x)=3x^2
\end{align*}
$$
これを
$$
\begin{align*}
(x^3)'=3x^2
\end{align*}
$$
と表すこともあります。
微分の公式
ここまでの結果をまとめてみましょう。
$${f(x)=x}$$ を微分すると $${f'(x)=1}$$
$${f(x)=x^2}$$ を微分すると $${f'(x)=2x}$$
$${f(x)=x^3}$$ を微分すると $${f'(x)=3x^2}$$
以上のことを一般化して、次のように公式化することができます。
<微分の公式1>
$${n}$$ は自然数($${n=1, 2, 3, \cdots}$$)のとき、
$${f(x)=x^n}$$ を微分すると
$$
\begin{align*}
f'(x)=nx^{n-1}
\end{align*}
$$
これを、次にように表すこともあります。
$$
\begin{align*}
(x^n)'=nx^{n-1}
\end{align*}
$$
ただし、$${n}$$ は自然数($${n=1, 2, 3, \cdots}$$)。
***
$${f(x)=x^n}$$ を微分すると、指数(肩にある数)$${n}$$ が係数になり、微分後の指数は $${1}$$ だけ減って $${n-1}$$ になります。

この公式をそのまま適用すれば
$${f(x)=x^4}$$ を微分すると
$$
\begin{align*}
f'(x)=4x^{4-1}=4x^3
\end{align*}
$$
$${f(x)=x^5}$$ を微分すると
$$
\begin{align*}
f'(x)=5x^{5-1}=5x^4
\end{align*}
$$
$${\hspace{37pt}\vdots}$$
$${f(x)=x^{10}}$$ を微分すると
$$
\begin{align*}
f'(x)=10x^{10-1}=10x^9
\end{align*}
$$
以下同様と、形式的に微分できます。導関数の定義
$$
\begin{align*}
f'(x)=\lim_{h\,\rightarrow\,0}\dfrac{f(x+h)-f(x)}{h}
\end{align*}
$$
に従って計算することも可能ですが、この微分の公式を使えば簡単に計算することができます。わざわざ導関数の定義に戻る必要はありません。
この公式の延長として、いろいろな関数の微分が次のように計算可能です。
$${f(x)=4x^3}$$ を微分すると
$$
\begin{align*}
f'(x)=&4\cdot(x^3)'\\
=&4\cdot3x^2\\
=&12x^2
\end{align*}
$$
係数 $${4}$$ は微分 $${( )'}$$ の外に出し、$${x^3}$$ の部分を微分します。
$${f(x)=2x^3+5x^2-4x}$$ を微分すると
$$
\begin{align*}
f'(x)&=2\cdot(x^3)'+5\cdot(x^2)'-4\cdot(x)'\\
&=2\cdot3x^2+5\cdot2x-4\cdot1\\
&=6x^2+10x-4
\end{align*}
$$
いくつかの関数のたし算ひき算で表されている場合は、それぞれの関数を別々に微分します。
これらは次のように公式化されます。微分するときは、これらの公式を用います。
<微分の公式2>
1. $${k}$$ を定数(実数)とするとき
$${y=kf(x)}$$ ならば $${y'=kf'(x)}$$
2. $${y=f(x)+g(x)}$$ ならば $${y'=f'(x)+g'(x)}$$
3. $${y=f(x)-g(x)}$$ ならば $${y'=f'(x)-g'(x)}$$
4. $${k, l}$$ を定数(実数)とするとき
$${y=kf(x)+lg(x)}$$ ならば $${y'=kf'(x)+lg'(x)}$$
***
1. 2. 3. を一般化したのが 4. です。
直感的に理解しやすいので割愛しますが、これらも導関数の定義に従って証明されます。
なお、上記では指数部分 $${n}$$ は自然数としていますが、次のように実数まで拡張することが可能です(高校の数学Ⅲの微分積分で習います)。
<微分の公式3>
$${\alpha}$$ を任意の実数とするとき、$${f(x)=x^{\alpha}}$$ を微分すると
$$
\begin{align*}
f'(x)=\alpha x^{\alpha-1}
\end{align*}
$$
***
(例1)$${f(x)=x^{\frac{3}{2}}}$$ を微分すると
$$
\begin{align*}
f'(x)=\dfrac{3}{2}x^{\frac{3}{2}-1}=\dfrac{3}{2}x^{\frac{3}{2}-\frac{2}{2}}=\dfrac{3}{2}x^{\frac{1}{2}}
\end{align*}
$$
(例2)$${f(x)=x^{\sqrt{2}}}$$ を微分すると
$$
\begin{align*}
f'(x)=\sqrt{2}x^{\sqrt{2}-1}
\end{align*}
$$
定数関数の微分
例えば $${f(x)=3}$$ という関数を考えます。これは
$${f(1)=3}$$
$${f(2)=3}$$
$${f(3)=3}$$
$${\hspace{18pt}\vdots}$$
と、$${x}$$ に何を代入しても定数 $${3}$$ となる関数です。このような関数を定数関数といいます。定数関数は、微分すると常に $${0}$$ になります。
例えば、先ほどの定数関数 $${f(x)=3}$$ を微分すると
$${f'(x)=0}$$
です。確認のため、定数関数の微分が $${0}$$ になることを、導関数の定義に従って証明します。
(証明)
$${f(x)=C\hspace{-5pt}}$$(定数)とすると
$${f(x+h)=C}$$(定数関数なので $${C}$$ のまま)
より
$$
\begin{align*}
f'(x)&=\lim_{h\,\rightarrow\,0}\dfrac{f(x+h)-f(x)}{h}\\
&=\lim_{h\,\rightarrow\,0}\dfrac{C-C}{h}\\
&=\lim_{h\,\rightarrow\,0}\dfrac{0}{h}\\
&=\lim_{h\,\rightarrow\,0}0\\
&=0
\end{align*}
$$
よって、$${f(x)=C\hspace{-5pt}}$$(定数)を微分すると
$$
\begin{align*}
f'(x)=0
\end{align*}
$$
これを
$$
\begin{align*}
(c)'=0
\end{align*}
$$
と表すこともあります。
(例)$${f(x)=7}$$ を微分すると $${f'(x)=0}$$
これを、$${(7)'=0}$$ と表すこともあります。
確認として、練習問題とその解答を与えます。
練習問題
次の式を微分しなさい。
(1) $${f(x)=6x^5}$$
(2) $${f(x)=-3x^4+2x^3-4x+5}$$
(解答)
(1)
$$
\begin{align*}
f'(x)&=6\cdot(x^5)'\\
&=6\cdot5x^4\\
&=30x^4
\end{align*}
$$
(2)
$$
\begin{align*}
f'(x)&=-3\cdot(x^4)'+2\cdot(x^3)'-4\cdot(x)'+(5)'\\
&=-3\cdot4x^3+2\cdot3x^2-4\cdot1+0\\
&=-12x^3+6x^2-4
\end{align*}
$$
導関数のいろいろな表記方法
関数 $${y=f(x)}$$ の導関数 $${f'(x)}$$ は、次のように表すこともあります。
$$
\begin{align*}
\dfrac{df(x)}{dx}, \dfrac{d}{dx}f(x), y', \dfrac{dy}{dx}, \dfrac{d}{dx}y
\end{align*}
$$
例えば、$${f(x)=x^3}$$ の導関数は次のように表せます。
$$
\begin{align*}
\dfrac{df(x)}{dx}&=3x^2\\
\dfrac{d}{dx}f(x)&=3x^2
\end{align*}
$$
$${\dfrac{df(x)}{dx}}$$ は ”ディー $${f(x)}$$ ディー $${x}$$” と読みます。
また、$${\dfrac{d}{dx}f(x)}$$ は ”ディー ディー $${x}$$ $${f(x)}$$” と読みます。
分数の形をしていますが、分数ではないので上から読み上げます。
さらに、$${y=x^3}$$ と与えられた場合は、その微分は $${y}$$ を用いて次のように表せます。
$$
\begin{align*}
y'&=3x^2\\
\dfrac{dy}{dx}&=3x^2\\
\dfrac{d}{dx}y&=3x^2
\end{align*}
$$
この $${\dfrac{d}{dx}}$$ という分数表記のメリットは、$${\dfrac{d}{dx}}$$ の分母の $${x}$$ を見ることによって、「$${x}$$ で微分する」ということがはっきりと分かることです。今の時点では必要性を感じませんが、最後に述べる偏微分でその必要性が分かります。
いろいろな関数の微分
ここでは、いろいろな関数の微分を紹介します。これらは公式として用いられます。いずれも導関数の定義に従えば証明できますが、ここでは結果だけを列挙します(高校の数学Ⅲの微分積分で習います)。
<三角関数の微分>
$${(\sin x)'=\cos x}$$
$${(\cos x)'=-\sin x}$$
$${(\tan x)'=\dfrac{1}{\cos^2x}}$$
<対数関数の微分>
$${(\log_a x)'=\dfrac{1}{x\log a}}$$($${a}$$ は $${1}$$ でない正の定数)
$${(\log x)'=\dfrac{1}{x}}$$
なお、$${\log x}$$ は $${e}$$ を底とする対数で
$${\log_e x=\log x}$$
と $${e}$$ を省略して書くのが普通です。この $${e}$$ は $${e=2.71828 \cdots}$$ となる無理数の定数で、ネイピア数(Napier's constant)とよばれています。
この $${e}$$ を低とする対数 $${\log x}$$ を、$${x}$$ の自然対数といいます。
また、$${10}$$ を低とする対数 $${\log_{10} x}$$ を、$${x}$$ の常用対数といいます。
<指数関数の微分>
$${(a^x)'=a^x\log a}$$($${a}$$ は $${1}$$ でない正の定数)
$${(e^x)'=e^x}$$
最後の $${e^x}$$ は、微分しても変化しない関数です。先に書いたように、$${e}$$ は無理数の定数(ネイピア数)です。
数学、物理、工学など、勉強が進めばこの $${e^x}$$ が重要な役割を演じることになるので、最後の
$$
\begin{align*}
(e^x)'=e^x(微分しても変わらない)
\end{align*}
$$
は特に押さえておきましょう。
高次導関数
関数 $${y=f(x)}$$ の導関数 $${f'(x)}$$ のさらに導関数を、$${f(x)}$$ の第2次導関数といい、次のように表します。
$$
\begin{align*}
y'', \dfrac{d^2y}{dx^2}, \dfrac{d^2}{dx^2}y, f''(x), \dfrac{d^2f(x)}{dx^2}, \dfrac{d^2}{dx^2}f(x)
\end{align*}
$$
つまり、関数 $${f(x)}$$ を2回連続して微分すると第2次導関数 $${f''(x)}$$ が得られます。
$$
\begin{align*}
\\[-14pt]
f(x) \xrightarrow[]{\hspace{-3pt}1回目の微分} f'(x) \xrightarrow[]{\hspace{-3pt}2回目の微分} f''(x)
\end{align*}
$$
「$${''}$$」は ”ダブルプライム” や ”ツーダッシュ” と読みます。
これに対して、$${f'(x)}$$ を $${f(x)}$$ の第1次導関数といいます。
関数 $${f(x)}$$ から第2次導関数 $${f''(x)}$$ を求めることを、$${f(x)}$$ を2階微分するといいます。
例えば、$${f(x)=2x^5+4x^3}$$ の第1次導関数は
$$
\begin{align*}
f'(x)&=2(x^5)'+4(x^3)'\\
&=2\cdot5x^4+4\cdot3x^2\\
&=10x^4+12x^2
\end{align*}
$$
なので、$${f(x)=2x^5+4x^3}$$ の第2次導関数は、この $${f'(x)}$$ をもう一度微分して
$$
\begin{align*}
f''(x)&=10(x^4)'+12(x^2)'\\
&=10\cdot4x^3+12\cdot2x\\
&=40x^3+24x
\end{align*}
$$
さらに、第2次導関数 $${f''(x)}$$ の導関数を、$${f(x)}$$ の第3次導関数といい、次のように表します。
$$
\begin{align*}
y''', \dfrac{d^3y}{dx^3}, \dfrac{d^3}{dx^3}y, f'''(x), \dfrac{d^3f(x)}{dx^3}, \dfrac{d^3}{dx^3}f(x)
\end{align*}
$$
つまり、関数 $${f(x)}$$ を3回連続して微分すると第3次導関数 $${f'''(x)}$$ が得られます。
$$
\begin{align*}
\\[-14pt]
f(x) \xrightarrow[]{\hspace{-3pt}1回目の微分} f'(x) \xrightarrow[]{\hspace{-3pt}2回目の微分} f''(x) \xrightarrow[]{\hspace{-3pt}3回目の微分} f'''(x)
\end{align*}
$$
「$${'''}$$」は ”トリプルプライム” や ”スリーダッシュ” と読みます。
関数 $${f(x)}$$ から第3次導関数 $${f'''(x)}$$ を求めることを、$${f(x)}$$ を3階微分するといいます。
一般に、関数 $${y=f(x)}$$ を $${n}$$ 回だけ微分して得られる関数を $${f(x)}$$ の第 $${\bm{n}}$$ 次導関数といい、次のように表します。
$$
\begin{align*}
y^{(n)}, \dfrac{d^{n}y}{dx^{n}}, \dfrac{d^n}{dx^n}y, f^{(n)}(x), \dfrac{d^nf(x)}{dx^n}, \dfrac{d^n}{dx^n}f(x)
\end{align*}
$$
関数 $${f(x)}$$ から第 $${n}$$ 次導関数 $${f^{(n)}(x)}$$ を求めることを、$${f(x)}$$ を $${\bm{n}}$$階微分するといいます。
第2次以上の導関数をまとめて高次導関数といいます。
高次導関数は微分記号「 ′ 」を用いてもよいですが、長く続くと見にくいので、より高次の場合は $${y^{(4)}}$$、$${f^{(4)}(x)}$$ などとカッコ付きの数字を用いて表すと便利です。
例えば、先ほどの $${y=2x^5+4x^3}$$ について
$$
\begin{align*}
f'(x)&=2\cdot5x^4+4\cdot3x^2=10x^4+12x^2\\
f''(x)&=10\cdot4x^3+12\cdot2x=40x^3+24x\\
f'''(x)&=40\cdot3x^2+24\cdot1=120x^2+24\\
f^{(4)}(x)&=120\cdot2x+0=240x\\
f^{(5)}(x)&=240\cdot1=240\\
f^{(6)}(x)&=0\\
\end{align*}
$$
練習問題
次の関数について、第5次導関数 $${\dfrac{d^5f(x)}{dx^5}}$$ を求めなさい。
(1) $${f(x)=x^4+x^3+x^2+x+1}$$
(2) $${f(x)=e^x}$$
(解答)
(1)
$$
\begin{align*}
\dfrac{df(x)}{dx}&=4x^3+3x^2+2x+1+0=4x^3+3x^2+2x+1\\
\dfrac{d^2f(x)}{dx^2}&=4\cdot3x^2+3\cdot2x+2\cdot1+0=12x^2+6x+2\\
\dfrac{d^3f(x)}{dx^3}&=12\cdot2x+6\cdot1+0=24x+6\\
\dfrac{d^4f(x)}{dx^4}&=24\cdot1+0=24\\
\dfrac{d^5f(x)}{dx^5}&=0\\
\end{align*}
$$
(2) $${e^x}$$ は微分しても変わらないので
$$
\begin{align*}
\dfrac{df(x)}{dx}&=e^x\\
\dfrac{d^2f(x)}{dx^2}&=e^x\\
\dfrac{d^3f(x)}{dx^3}&=e^x\\
\dfrac{d^4f(x)}{dx^4}&=e^x\\
\dfrac{d^5f(x)}{dx^5}&=e^x\\
\end{align*}
$$
偏微分
本文でやった
$${f(x)=x^2}$$
という関数は、変数が $${x}$$ だけの1変数関数です。これを微分すると
$$
\begin{align*}
f'(x)=2x
\end{align*}
$$
または
$$
\begin{align*}
(x^2)'&=2x\\
\dfrac{df(x)}{dx}&=2x\\
\dfrac{d}{dx}f(x)&=2x
\end{align*}
$$
と表せることを先に解説しました。
2変数関数
関数には、次のように変数が $${2}$$ つの関数もあります。これを2変数関数といいます。
$$
\begin{align*}
f(x, y)=3x^2y^5
\end{align*}
$$
これは、$${x, y}$$ の2つの変数をもつ関数です。$${x, y}$$ の値が決まると、$${z=f(x, y)}$$ という関数によって $${z}$$ の値がただ1つに決まります。
$$
\begin{align*}
x, y が決まる \xrightarrow[]{ z=f(x, y) } z の値がただ1つに決まる
\end{align*}
$$
(例)$${f(x, y)=3x^2y^5}$$ について
$${x=2, y=1}$$ のとき
$${f(2, 1)=3\cdot2^2\cdot1^5=3\cdot4\cdot1=12}$$
2変数関数の微分
ここで、$${f(x, y)=3x^2y^5}$$ の微分を考えます。この場合、次のように2つの微分があります。
➀ $${y}$$ を定数(数)とみなして $${x}$$ で微分する。
これは、$${\dfrac{\partial f(x, y)}{\partial x}}$$ という記号を用いて
$$
\begin{align*}
\dfrac{\partial f(x, y)}{\partial x}&=\dfrac{\partial}{\partial x}3x^2y^5\\
&=3y^5\dfrac{d}{dx}x^2\\
&=3y^5\cdot2x\\
&=6xy^5
\end{align*}
$$
より
$$
\begin{align*}
\dfrac{\partial f(x, y)}{\partial x}=6xy^5
\end{align*}
$$
これを、次のように表すこともあります。
$$
\begin{align*}
\dfrac{\partial}{\partial x}f(x, y)=6xy^5
\end{align*}
$$
$${y}$$ を定数(数)とみなし、$${x}$$ の関数部分を $${x}$$ で微分します。

$${y}$$ は定数(数)扱いなので、$${3y^5}$$ をまとめて係数として扱い、微分 $${\dfrac{d}{dx}}$$ の外に出します。
このように、2変数関数に関して、1つの変数を定数とみなし、もう1つの変数で微分したものを偏微分といいます。
偏微分の記号
偏微分で使う「$${\partial}$$」という記号は、筆記体の「$${d}$$」("ディー")が元になっており、”ラウンドディー” や ”デル” と読みます。
偏微分を表すにあたって
$${\dfrac{\partial f(x, y)}{\partial x}}$$ や $${\dfrac{\partial}{\partial x}f(x, y)}$$
の分母の $${x}$$ を見ることによって、$${x}$$ で偏微分することがはっきりと明示されます。これを、分母を $${y}$$ にして
$${\dfrac{\partial f(x, y)}{\partial y}}$$ や $${\dfrac{\partial}{\partial y}f(x, y)}$$
と書けば、以下で述べる「$${y}$$ で偏微分する」という意味になります。
$${f(x, y)=3x^2y^5}$$ について
➁ $${x}$$ を定数(数)とみなして $${y}$$ で微分(偏微分)する。
$$
\begin{align*}
\dfrac{\partial f(x, y)}{\partial y}&=\dfrac{\partial}{\partial y}3x^2y^5\\
&=3x^2\dfrac{d}{dy}y^5\\
&=3x^2\cdot5y^4\\
&=15x^2y^4
\end{align*}
$$
より
$$
\begin{align*}
\dfrac{\partial f(x, y)}{\partial y}=15x^2y^4
\end{align*}
$$
これを、次のように表すこともあります。
$$
\begin{align*}
\dfrac{\partial}{\partial y}f(x, y)=15x^2y^4
\end{align*}
$$
$${x}$$ を定数(数)とみなし、$${y}$$ の関数部分を $${y}$$ で微分します。

$${x}$$ は定数(数)扱いなので、$${3x^2}$$ をまとめて係数として扱い、微分 $${\dfrac{d}{dy}}$$ の外に出します。
このように、$${f(x, y)=3x^2y^5}$$ について
➀ $${x}$$ で偏微分すると
$$
\begin{align*}
\dfrac{\partial f(x, y)}{\partial x}=3\cdot2x\cdot y^5=6xy^5
\end{align*}
$$
➁ $${y}$$ で偏微分すると
$$
\begin{align*}
\dfrac{\partial f(x, y)}{\partial y}=3x^2\cdot5y^4=15x^2y^4
\end{align*}
$$
と、結果が異なることに注意しましょう。
多変数関数の偏微分
3変数以上の関数についても偏微分を考えることができます。
変数が2つ以上の関数を多変数関数といいます。多変数関数の偏微分は、ある1つの変数のみに着目し、それ以外の変数は定数とみなして微分します。
(例1)$${f(x, y, z)=5x^2y^3+z^4}$$ について $${x}$$ で偏微分すると
$$
\begin{align*}
\dfrac{\partial}{\partial x}f(x, y, z)&=\dfrac{\partial}{\partial x}(5x^2y^3+z^4)\\
&=\dfrac{\partial}{\partial x}5x^2y^3+\dfrac{\partial}{\partial x}z^4\\
&=5y^3\dfrac{d}{dx}x^2+0\\
&=5y^3\cdot2x\\
&=10xy^3
\end{align*}
$$
$${z}$$ は定数とみなしているので
$$
\begin{align*}
\dfrac{\partial}{\partial x}z^4=0
\end{align*}
$$
となります。
(例2)$${f(x, y, z)=5x^2y^3+z^4}$$ について $${z}$$ で偏微分すると
$$
\begin{align*}
\dfrac{\partial}{\partial x}f(x, y, z)&=\dfrac{\partial}{\partial x}(5x^2y^3+z^4)\\
&=\dfrac{\partial}{\partial x}5x^2y^3+\dfrac{\partial}{\partial x}z^4\\
&=0+4z^3\\
&=4z^3
\end{align*}
$$
$${x, y}$$ は定数とみなしているので
$$
\begin{align*}
\dfrac{\partial}{\partial x}5x^2y^3=0
\end{align*}
$$
となります。
(参考1)数の分類
数の分類は以下の通りです。
$$
\begin{align*}
\boldsymbol{複素数 a+bi}
\begin{cases}
\overset{\small b=0 のとき}{\boldsymbol{実数 a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数} \scriptsize{(1, 2, 3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数} \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
{\footnotesize 例 0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize(循環する無限小数)}}\\
{\footnotesize 例 0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
{\scriptsize 例 \pi (=3.1415\cdots) のような \boldsymbol{循環しない無限小数}}\\
{\scriptsize e (=2.7182\cdots) のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0 のとき}{\boldsymbol{虚数 a+bi}} 特に a=0 のとき \boldsymbol{bi} を\boldsymbol{純虚数}という。
\end{cases}
\end{align*}
$$
(コメント)
以下の数式小説で微分法が現れます。
次は積分法を執筆中です。
