
もっと分かりやすく②「対称性の破壊」
本題である「対称性の破壊」に入る前に、対称式、対称式の基本定理、解と係数の関係について復習をします。
(復習)対称式について
対称式とは文字を入れ替えても変化しない式です。例えば
$${\alpha+\beta}$$ や $${\alpha\beta}$$
は、$${\alpha}$$ と $${\beta}$$ を入れ替えても式は変化しないので、対称式となります(本シリーズ(4))。
$$
{\begin{align*}
\alpha+\beta&=\beta+\alpha &\Leftarrow 変化しない\\
\alpha\beta&=\beta\alpha &\Leftarrow 変化しない
\end{align*}}
$$
$${2+3}$$ と $${3+2}$$ は同じ、$${2 \times 3}$$ と $${3 \times 2}$$ も同じ値となることと同じ発想です。しかし、$${\alpha-\beta}$$ は対称式ではありません。$${\alpha}$$ と $${\beta}$$ を入れ替えると式が変化し、違う式となります。
$$
{\begin{align*}
\alpha-\beta \ne \beta-\alpha \Leftarrow 変化する
\end{align*}}
$$
$${2-3}$$ と $${3-2}$$ が違う値になることと同じ発想です。
さらに対称式として、例えば $${\alpha^2+\beta^2}$$ があります。これも、$${\alpha}$$ と $${\beta}$$ を入れ替えても式は変化せず、同じ式になります。
$$
{\begin{align*}
\alpha^2+\beta^2=\beta^2+\alpha^2 \Leftarrow 変化しない
\end{align*}}
$$
しかし、$${\alpha^2-\beta^2}$$ は対称式にはなりません。$${\alpha}$$ と $${\beta}$$ を入れ替えると式が変化します。
$$
{\begin{align*}
\alpha^2-\beta^2\ne\beta^2-\alpha^2 \Leftarrow 変化する
\end{align*}}
$$
では $${(\alpha-\beta)^2}$$ は対称式でしょうか?$${\alpha}$$ と $${\beta}$$ を入れ替えると
$$
{\begin{align*}
(\alpha-\beta)^2=(\beta-\alpha)^2 \Leftarrow 変化しない
\end{align*}}
$$
となり、対称式となります。$${\alpha}$$ と $${\beta}$$ を入れ替えると、$${\alpha-\beta}$$ は符号が変わるので対称式ではありません。しかし、それを2乗した $${(\alpha-\beta)^2}$$ は対称式です。2乗するとマイナスはプラスになるので、変化しないということです。
他にも、対称式には以下のようなものがあります。
$${(\alpha+\beta)^2}$$
$${(\alpha+\beta)^3}$$
$${\alpha^3+\beta^3}$$
$${\dfrac{1}{a}+\dfrac{1}{\beta}}$$
特に、$${\alpha+\beta}$$ と $${\alpha\beta}$$ は、最も基本的な対称式ということで基本対称式といいます。そこで、この基本対称式について次のような定理があります。
(復習)対称式の基本定理について
<対称式の基本定理>
全ての対称式は基本対称式の加減乗除で表すことができる。
加減乗除とは「足し算、引き算、掛け算、割り算」のことです。つまり、$${\alpha^2+\beta^2}$$ のようなすべての対称式は、基本対称式 $${\alpha+\beta, \alpha\beta}$$ の「足し算、引き算、掛け算、割り算」で表すことができます(本シリーズ(4))。
例えば、対称式 $${\alpha^2+\beta^2}$$ は、因数分解公式
$${\alpha^2+2\alpha\beta+\beta^2=(\alpha+\beta)^2}$$
について、$${2\alpha\beta}$$ を左辺に移項して
$$
\begin{align*}
\alpha^2+\beta^2=(\hspace{-5.5pt}\underset{基本対称式}{\underline{\alpha+\beta}}\hspace{-5.5pt})^2-2\hspace{-10pt}\underset{基本対称式}{\underline{\alpha\beta}}
\end{align*}
$$
とすれば、基本対称式の加減乗除で表すことができます。
(復習)解と係数の関係について
2次方程式 $${ax^2+bx+c=0}$$ について、2つの解を $${\alpha, \beta}$$ とすると、次のことが成り立ちます。なお、簡単のため係数 $${a, b, c}$$ の範囲は有理数とします(本シリーズ(18))。
<解と係数の関係>
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
これは、2次方程式の解 $${\alpha, \beta}$$ が分からなくても、その和と積は係数を用いて表すことができるという公式です(本シリーズ(4))。
ここで、この関係式の両辺を入れ替えて
$$
\begin{align*}
-\dfrac{b}{a}&=\alpha+\beta\\[8pt]
\dfrac{c}{a}&=\alpha\beta
\end{align*}
$$
上の式の両辺に $${-1}$$ をかけると
$$
\begin{align*}
\begin{align*}
\dfrac{b}{a}&=-(\alpha+\beta)\\[8pt]
\dfrac{c}{a}&=\alpha\beta
\end{align*}
\cdots (*)
\end{align*}
$$
となり、係数の分数 $${\dfrac{b}{a}, \dfrac{c}{a}}$$ は対称式で表されることがわかります。
ここで、前回やった集合 $${Q_2}$$ について復習します。$${Q_2}$$ とは
$${Q_2=}$${2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で構成できるすべての式の集合}
でした。すると、この $${Q_2}$$ は、すべての対称式の集合と一致することがわかります。
集合 $${Q_2=}$$ すべての対称式の集合
その理由は(注1)で簡単に述べておくので、本文ではこれを認めた上で次に進みます。
2次方程式での「対称性の破壊」
ここから、前回のシリーズ (18) <もっと分かりやすく①「累乗根の添加」>で、集合 $${Q_2}$$ に添加した
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
について、その平方根の中身
$${\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}$$
を考えます。先ほどの<解と係数の関係>を用いれば、この式を2次方程式の解 $${\alpha, \beta}$$ を用いて表すことができます。以下、それを示していきます。
まずはこれに、先ほどの<解と係数の関係>
$$
\begin{align*}
\dfrac{b}{a}&=-(\alpha+\beta)\\[8pt]
\dfrac{c}{a}&=\alpha\beta
\end{align*}
$$
を代入すると
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{1}{4}\left(\alpha+\beta\right)^2-\alpha\beta\\
&=\dfrac{1}{4}\left(\alpha+\beta\right)^2-\dfrac{4}{4}\alpha\beta\\
&=\dfrac{\left(\alpha+\beta\right)^2-4\alpha\beta}{4}\\
&=\dfrac{\alpha^2+2\alpha\beta+\beta^2-4\alpha\beta}{4}\\
&=\dfrac{\alpha^2+2\alpha\beta-4\alpha\beta+\beta^2}{4}\\
&=\dfrac{\alpha^2-2\alpha\beta+\beta^2}{4}\\
&=\dfrac{(\alpha-\beta)^2}{4}
\end{align*}
$$
より
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{(\alpha-\beta)^2}{4} \cdots ①
\end{align*}
$$
するとこの式は対称式となっています。対称式とは
「文字を入れ替えても変化しない式」
でした。実際 $${\alpha}$$ と $${\beta}$$ を入れ替えてみると
$$
\begin{align*}
\dfrac{(\alpha-\beta)^2}{4}=\dfrac{(\beta-\alpha)^2}{4} \Leftarrow 変化しない
\end{align*}
$$
と変化しないので、対称式となります。先ほどやった $${(\alpha-\beta)^2}$$ が対称式であることと同じ理屈です。
では添加された平方根
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
は対称式でしょうか。これは対称式ではありません。なぜなら、この式を変形していくと
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\sqrt{\dfrac{(\alpha-\beta)^2}{4}}\\
&=\sqrt{\dfrac{1}{4}(\alpha-\beta)^2}\\
&=\sqrt{\left(\dfrac{1}{2}\right)^2(\alpha-\beta)^2}\\
&=\dfrac{1}{2}\sqrt{(\alpha-\beta)^2}\\[7pt]
&=
\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}\{-(\alpha-\beta)\}
\end{cases} \cdots (*)\\[22pt]
&=
\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}(\beta-\alpha)
\end{cases}
\end{align*}
$$
より
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
=\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}(\beta-\alpha)
\end{cases} \cdots ②
\end{align*}
$$
なお、$${(*)}$$ のところで
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
=
\begin{cases}
\alpha-\beta\\
-(\alpha-\beta)
\end{cases}
\end{align*}
$$
という公式を使っています(証明は割愛。高校の複素数の知識を使う)。
すると
$${\dfrac{1}{2}(\alpha-\beta)}$$ と $${\dfrac{1}{2}(\beta-\alpha)}$$
はどちらも対称式ではないことがわかります。$${\alpha}$$ と $${\beta}$$ を入れ替えると、どちらも式が変わってしまいます。
$$
{\begin{align*}
\dfrac{1}{2}(\alpha-\beta) \ne \dfrac{1}{2}(\beta-\alpha) \Leftarrow 変化する\\[10pt]
\dfrac{1}{2}(\beta-\alpha) \ne \dfrac{1}{2}(\alpha-\beta) \Leftarrow 変化する
\end{align*}}
$$
よって
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
は対称式ではないことがわかりました。このことをまとめると
$${\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}$$
は対称式ですが、その平方根をとった
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
は対称式ではないことになります。
2次置換について
以上のことを、2次方程式の解 $${\alpha, \beta}$$ の入れ替えと結び付けて考えてみます。この文字の入れ替えのことを置換といいます。特に今回は2つの文字の置換なので2次置換といいます。教科書では2次の置換と書かれている場合が多いですが、本シリーズでは2次置換という言葉を使います。
2次方程式 $${ax^2+bx+c=0}$$ の2つの解 $${\alpha, \beta}$$ について、この2次置換は、次の (case1) と (case2) の2通りがあります。
(case1) $${\dbinom{\alpha \beta}{\alpha \beta}}$$
(case2) $${\dbinom{\alpha \beta}{\beta \alpha}}$$
それぞれについて詳しくみていきます。
(case1) $${\dbinom{\alpha \beta}{\alpha \beta}}$$ について
これは $${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に置き換える、つまり何も変化しない置換です。上から下へ変換すると読みます。
この何も変化させない置換を恒等置換といいます。恒等置換は $${I}$$ という記号を用いて、次のように表記されます。
$${\dbinom{\alpha \beta}{\alpha \beta}=I}$$
(case2) $${\dbinom{\alpha \beta}{\beta \alpha}}$$ について
これは $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換です。これも上から下へ変換すると読みます。
これは $${\alpha}$$ と $${\beta}$$ の入れ替えで、そのような置換を互換といいます。互換は $${(\alpha \beta)}$$ と表記されます。
$${\dbinom{\alpha \beta}{\beta \alpha}=(\alpha \beta)}$$
2次置換は、この2つの $${I}$$ と $${(\alpha \beta)}$$ がすべてで他にはありません。ここで先ほどの $${①}$$ 式
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{(\alpha-\beta)^2}{4} \cdots ①
\end{align*}
$$
をみてみます。先ほど解説したようにこれは対称式なので、2次置換 $${I}$$ と $${(\alpha \beta)}$$ を作用させても変化しません。
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{(\alpha-\beta)^2}{4}\\[10pt]
&\hspace{1pt}\Downarrow \leftarrow I と (\alpha \beta) を作用\\[5pt]
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{(\alpha-\beta)^2}{4} \leftarrow 変化しない
\end{align*}
$$
ところが、この平方根をとった $${②}$$ 式
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\sqrt{\dfrac{(\alpha-\beta)^2}{4}}\\
&=
\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}(\beta-\alpha)
\end{cases} \cdots ②
\end{align*}
$$
はどうでしょうか。先ほど解説したようにこれは対称式ではないので、2次置換のうち、恒等置換 $${I}$$ では変化しませんが、互換 $${(\alpha \beta)}$$ では変化してしまいます。
恒等置換 $${I}$$ を作用させると
$$
\begin{align*}
&\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
=\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}(\beta-\alpha)
\end{cases}\\[25pt]
&\hspace{68pt}\Downarrow \leftarrow I を作用\\[5pt]
&\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
=\begin{cases}
\dfrac{1}{2}(\alpha-\beta) \leftarrow 変化しない\\[8pt]
\dfrac{1}{2}(\beta-\alpha) \leftarrow 変化しない
\end{cases}
\end{align*}
$$
しかし、互換 $${(\alpha \beta)}$$ を作用させると、$${\alpha, \beta}$$ の入れ替えが入るので変化します。
$$
\begin{align*}
&\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
=\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}(\beta-\alpha)
\end{cases}\\[25pt]
&\hspace{68pt}\Downarrow \leftarrow (\alpha \beta) を作用\\[5pt]
&\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
=\begin{cases}
\dfrac{1}{2}(\beta-\alpha) \leftarrow 変化する\\[8pt]
\dfrac{1}{2}(\alpha-\beta) \leftarrow 変化する
\end{cases}
\end{align*}
$$
以上のことをまとめると、$${①}$$ 式
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{(\alpha-\beta)^2}{4} \cdots ①
\end{align*}
$$
は対称式なので、2次置換($${I}$$ と $${(\alpha \beta)}$$)を作用させても変化しません。しかし、その平方根をとった $${②}$$ 式
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\sqrt{\dfrac{(\alpha-\beta)^2}{4}}\\
&=
\begin{cases}
\dfrac{1}{2}(\alpha-\beta)\\[8pt]
\dfrac{1}{2}(\beta-\alpha)
\end{cases} \cdots ②
\end{align*}
$$
を変化させない置換は恒等置換 $${I}$$ のみとなり、 $${①}$$ から $${②}$$ にかけて、式の対称性(式を変化せない置換)が、2次置換から恒等置換へと破壊されています。その対称性の破壊を、平方根の添加による集合の拡大と関連付けることができます。
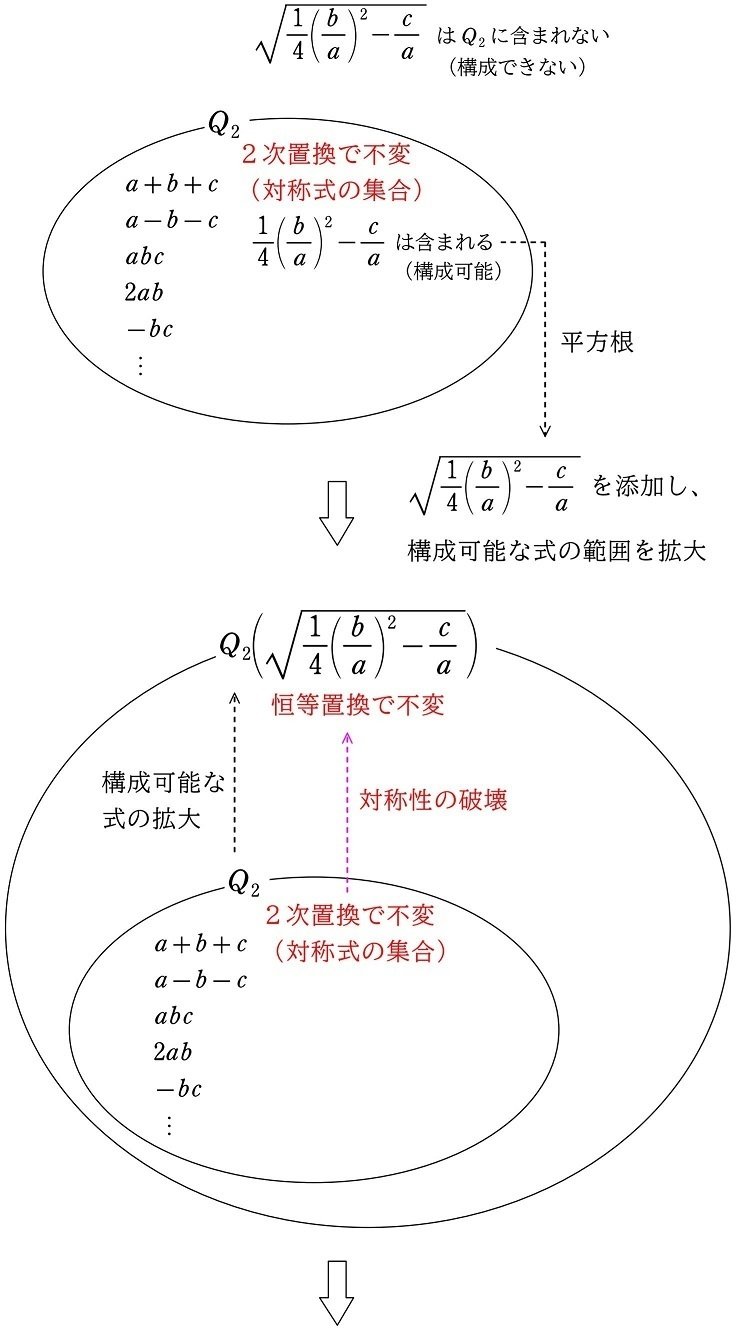
まず、集合 $${Q_2}$$ はすべての対称式の集合でした。すると、先ほどの
$${\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}$$
は対称式でなので、集合 $${Q_2}$$ の中で構成することができます。しかしその平方根
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
は対称式ではないので、集合 $${Q_2}$$ の中で構成することはできません。

そこで、$${Q_2}$$ に平方根
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$
を添加し、その集合を
$${Q_2\hspace{-2pt}\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$
とすると、その集合内で構成可能なすべての式の対称性(すべての式を変化させない置換)は、恒等置換のみとなります。つまり、集合が拡大するにつれて、対称性が2次置換から恒等置換にまで縮小(破壊)されているわけです。
以上をまとめると、簡単のため
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}=z}$$
とおき、$${Q_2}$$ に $${z}$$ を添加した集合を $${Q_2(z)}$$、つまり
$${Q_2\hspace{-2pt}\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)=Q_2(z)}$$
とおくと、次にように図式化できます。
$$
\begin{gather*}
\,\,Q_2\\
\hspace{35pt}拡大 \downarrow \Leftarrow z の添加\\
Q_2(z)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf 2次置換(対称式)}\\
\hspace{31pt}破壊 \downarrow \Leftarrow z の添加\\
{\bf 恒等置換}
\end{gather*}
$$
そして、恒等置換にまで対称性が破壊された最後の集合
$${Q_2\hspace{-2pt}\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)=Q_2(z)}$$
で、2次方程式の解の公式がはじめて構成できるようになります(注2)(注3)。

このことは3次方程式においても、さらには4次方程式や5次方程式など、高次の方程式においても同じ理屈です。数式の変形こそ難しくはなりますが、累乗根の添加によって対称性を破壊していく過程自体は同じものとなります。
では、今は2次方程式についてみてきましたが、3次方程式についてみてみましょう。
3次方程式での「対称性の破壊」
詳しくは本シリーズ (12), (13) に任せますが、3次方程式の場合の対称性の破壊は、2次方程式と違って、次のように途中に偶置換(偶置換シンメトリー)が入ります。偶置換とは偶数個の互換の積で表される置換です(本シリーズ(8))。構成可能な式の集合の拡大と対応して、次のように3段階の対称性の破壊が入るわけです。
$$
\begin{gather*}
Q(\omega)\\
\hspace{67pt}\downarrow \Leftarrow X_3 の添加\\
Q(\omega, X_3)\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
Q(\omega, X_3, A)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
{\bf 3次置換(対称式)}\\
\hspace{67pt}\downarrow \Leftarrow X_3 の添加\\
{\bf 偶置換シンメトリー}\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
{\bf 恒等置換}
\end{gather*}
$$
構成可能な式の集合が拡大するのと対応して、対称性が縮小(破壊)されていくことに注意してください。そして、恒等置換にまで対称性が破壊されたときに、その集合内で3次方程式の解の公式が構成可能となるわけです(注2)。

なお、上図の $${X_3}$$ は、3次方程式の解 $${\alpha, \beta, \gamma}$$ の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\beta)}$$
であり、$${A}$$ はラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
となります(本シリーズ (12)、(13)) 。
5次方程式での「対称性の破壊」
5次方程式の解の公式は、その集合内で構成可能なすべての式の対称性(すべての式を変化させない置換)は、5次置換から偶置換までしか破壊できないことが証明されます。破壊できるのは偶置換(偶置換シンメトリー)までで、それ以上は破壊できない。つまり恒等置換にまで破壊することができないことによって、解の公式が存在しないというのが、アーベルの証明(アーベル・ルフィニの証明)のアイデアとなります(本シリーズ (14)~(17))。

なお、上図の $${X_5}$$ は、5次方程式の解 $${x_1, x_2, x_3, x_4, x_5}$$ の差積
$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$
となります(本シリーズ (14))。
(注1)係数と有理数の加減乗除で構成される集合と、すべての対称式の集合が一致すること
$${Q_2=}$${2次方程式の係数 $${a, b, c}$$ と有理式の加減乗除で構成できるすべての式の集合}
について、この集合 $${Q_2}$$ が、すべての対称式の集合と一致すること(これを「定理A」とします)を証明します。つまり
集合 $${Q_2=}$$ すべての対称式の集合(定理A)

厳密な証明ではなく、具体例をつかった形で簡単に述べます。イメージがつかめればよいと思います。なお、$${2}$$ や $${-\dfrac{3}{4}}$$ のような任意の有理数(定数)は、どちらの集合にもすべて含まれているとします。
この「定理A」の証明(集合が一致することの証明)には、以下の (case1) と (case2) の2つを証明する必要があります。
(case1)
2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で構成された式ならば、その式は対称式である。
及び、その逆
(case2)
(有理数を係数として用いた)対称式ならば、それは2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で構成できる。
(証明のイメージ)

(case1) の簡単な証明
<解と係数の関係> を変形した、本文中 $${(*)}$$
$$
\begin{align*}
\begin{align*}
\dfrac{b}{a}&=-(\alpha+\beta)\\[8pt]
\dfrac{c}{a}&=\alpha\beta
\end{align*}
\cdots (*)
\end{align*}
$$
について、両辺に $${a}$$ をかけた
$$
\begin{align*}
b&=-(\alpha+\beta)a \cdots ①\\
c&=\alpha\beta a \cdots ②
\end{align*}
$$
を用意します。すると、例えば $${a+b+c}$$ は対称式になるでしょうか?これには、先ほどの $${①, ②}$$ を代入すれば
$$
\begin{align*}
a+b+c&=a-(\alpha+\beta)a+\alpha\beta a\\
&=\{1-(\alpha+\beta)+\alpha\beta\}a
\end{align*}
$$
と、有理数の定数 $${a}$$ と基本対称式 $${\alpha+\beta, \alpha\beta}$$ で表されるので、$${a+b+c}$$ は対称式となります。なお定数 $${a}$$ は、$${\alpha}$$ と $${\beta}$$ を入れ替えても変化しないので、残っていても問題ありません。
一般に、有理数と基本対称式の加減乗除で表されたすべての式は対称式となるので、集合 $${Q_2}$$ 内のすべての式は対称式となります。
(case2) の簡単な証明
これには<対称式の基本定理>を用います。<対称式の基本定理>より、対称式はかならず基本対称式の加減乗除で表すことができます。すると、その基本対称式に<解と係数の関係>
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
を代入すれば、必ず2次方程式の係数で表されます。例えば、対称式 $${\alpha^2+\beta^2}$$ について実践してみると、本文で示したように
$$
\begin{align*}
\alpha^2+\beta^2=(\hspace{-5.5pt}\underset{基本対称式}{\underline{\alpha+\beta}}\hspace{-5.5pt})^2-2\hspace{-10pt}\underset{基本対称式}{\underline{\alpha\beta}}
\end{align*}
$$
と基本対称式の加減乗除で表されるので、これに
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
を代入すれば
$$
\begin{align*}
\alpha^2+\beta^2&=(\alpha+\beta)^2-2\alpha\beta\\
&=\left\{-\left(\dfrac{b}{a}\right)\right\}^2-2\cdot\dfrac{c}{a}\\
&=\left(\dfrac{b}{a}\right)^2-\dfrac{2c}{a}\\
&=\dfrac{b^2}{a^2}-\dfrac{2ac}{a^2}\\
&=\dfrac{b^2-2ac}{a^2}
\end{align*}
$$
となり、これで2次方程式の係数 $${a, b, c}$$ と有理数(ここでは $${2}$$)で表すことができました。
一般に、(有理数が係数の)すべての対称式は基本対称式と有理数の加減乗除で表されるので(対称式の基本定理)、すべての対称式は集合 $${Q_2}$$ に含まれることがわかります。
以上により、(case1) と (case2) の両方が示されたことによって「定理A」が証明されました。
(注2)対称性を恒等置換にまで破壊する理由(復習)
解の公式を構成するにあたって、構成可能な式の対称性を、なぜ恒等置換まで破壊させる必要があるのか。その理由は、解の式 $${x_1, x_2, \cdots}$$ のすべてを変化せない置換は恒等置換のみだからです。例えば3次方程式の解 $${x_1, x_2, x_3}$$ に恒等置換を作用させても、$${x_1, x_2, x_3}$$ はいずれも変化しません。
$$
\begin{align*}
x_1 &x_2 x_3\\
&\downarrow {\small 恒等置換を作用}\\
x_1 &x_2 x_3 {\small \Leftarrow いずれも変化しない}
\end{align*}
$$
解の公式は文字通り解を表す式なので、解の式 $${x_1, x_2, \cdots}$$ と同等の対称性をもちます。解の公式を変化させない置換は恒等置換のみです。よって、次々と都合のいい式を添加していき、最終的に構成可能な式の対称性(式を変化させない置換)を恒等置換にまで破壊できれば、それまでに添加された式の加減乗除によって、はれて解の公式が実現できるわけです。
(注3)本シリーズとの違い
本シリーズ (11) では、2次方程式
$${ax^2+bx+c=0}$$
について、両辺を $${a\ne0}$$ で割って
$$
\begin{align*}
\dfrac{ax^2+bx+c}{a}&=\dfrac{0}{a}\\
\dfrac{ax^2}{a}+\dfrac{bx}{a}+\dfrac{c}{a}&=0\\
x^2+\dfrac{b}{a}x+\dfrac{c}{a}&=0
\end{align*}
$$
$${\dfrac{b}{a}=a_1, \dfrac{c}{a}=a_2}$$ と置いて
$$
\begin{align*}
x^2+a_1x+a_2=0
\end{align*}
$$
とし、2乗の係数を $${1}$$ としました。ここで、最初に考える加減乗除で閉じた集合を
$${Q=}$${係数 $${a_1, a_2}$$ と有理数の加減乗除で表されるすべての式の集合}
とし、この式に平方根 $${\sqrt{(a_1)^2-4a_1}}$$ を添加して・・・、という流れで本篇は議論しています。
こうすると、3つの係数の文字 $${a, b, c}$$ を $${a_1, a_2}$$ と2つに減らすことができ、今後の議論の見通しがよくなります。
なお添加する式は、2次方程式の解 $${\alpha, \beta}$$ の差積 $${X_2}$$ の平方根
$${\sqrt{(X_2)^2}=\sqrt{(\alpha-\beta)^2}}$$
を添加することと同じとなります(本シリーズ (11) )。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベント」による「3次方程式の解の公式」の導出
(8)「偶置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となることを解説
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「偶置換」にまで絞り込む(破壊する)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(破壊する)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から偶置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、偶置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての偶置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点的に解説。
(19)もっと分かりやすくシリーズ②「対称性の破壊」について重点的に解説。
