もっと分かりやすく➅「対称式ではない解の公式を基本対称式で表す」には？

（初めに）ここでは、分かりにくいと思った本シリーズ (11) の内容をもう一度解説していきます。
　なお、本シリーズ (11) では便宜的に「係数の置き換え」を行っていますが、ここでは行っていません。置き換えるか置き換えないかの違いだけで、本質的には同じです。
　本記事は『天才数学者はこう解いた、こう生きた』（木村俊一著）から引用を得るなど、大きく参考にしています。

（本文スタート）解の公式とは、解をその方程式の係数で表すことです。例えば２次方程式 $${ax^2+bx+c=0}$$ の解を $${\alpha,  \beta}$$ としたとき（簡単のため係数 $${a,  b,  c}$$ の範囲は有理数とする）、それらを係数 $${a,  b,  c}$$ と有理数を用いて表すことができれば、それが解の公式となります。なお、有理数を用いることは自明なので、以下「有理数を用いて」は省略する場合があります。

$$
\begin{align*}
\alpha&=係数  a,  b,  c  で表す\\
\beta&=係数  a,  b,  c  で表す\\
&\hspace{2pt}\downarrow\\
x&=係数  a,  b,  c  で表す（解の公式）
\end{align*}
$$

　ここでは、解の公式を係数 $${a, b, c}$$ で表すことについての困難性と、それを乗り越えていく過程を解説していきます。

解の公式の本質

　解の式 $${\alpha,  \beta}$$ は対称式ではありません。$${\alpha}$$ と $${\beta}$$ を入れ替えると、$${\alpha}$$ は $${\beta}$$ に、 $${\beta}$$ は $${\alpha}$$ に変化します。

$$
\begin{align*}
&\,\alpha\\
&\downarrow　\Leftarrow  \alpha  と  \beta  を入れ替える\\
&\,\beta（変化する）
\end{align*}
$$

$$
\begin{align*}
&\,\beta\\
&\downarrow　\Leftarrow  \alpha  と  \beta  を入れ替える\\
&\,\alpha（変化する）
\end{align*}
$$

　「２次方程式の係数 $${a,  b,  c}$$ の加減乗除で表されるすべての式の集合」と「すべての対称式の集合」が等しくなることは、本シリーズ (19) でやりました（注１で簡単に解説）。

　係数 $${a,  b,  c}$$ は基本対称式 $${\alpha+\beta,  \alpha\beta}$$（と有理数）で表されるので、いわば対称式の材料です（注１の前半より

$$
\begin{cases}
a  は有理数\\[5pt]
b=-(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})a\\[15pt]
c=\hspace{-12pt}\underbrace{\alpha\beta}_{基本対称式}\hspace{-10pt} a\hspace{28pt}
\end{cases}
$$

と表せます）。
　解の公式とは、対称式ではない $${\alpha,  \beta}$$ を、対称式の材料である係数 $${a,  b,  c}$$ を用いて表すという、一見矛盾とも思える課題を克服して実現しています。

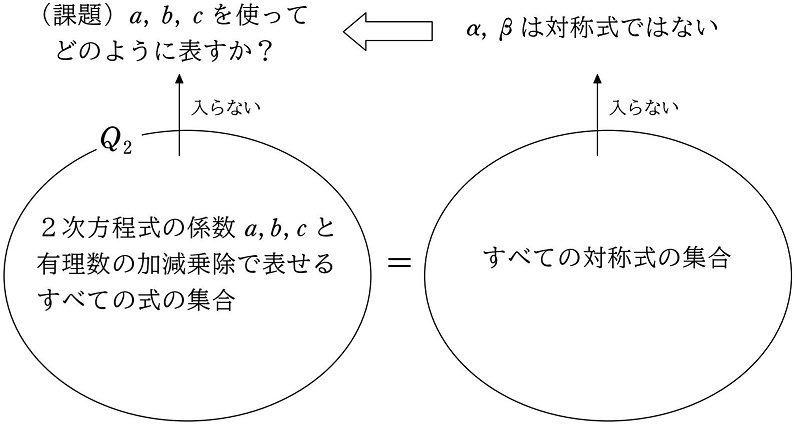
$$
\begin{align*}
\underbrace{\alpha}_{対称式でない}\hspace{-14pt}
&=係数  a,  b,  c（基本対称式）で表す\\
\underbrace{\beta}_{対称式でない}\hspace{-14pt}
&=係数  a,  b,  c（基本対称式）で表す\\
&\hspace{2pt}\downarrow\\
x&=係数  a,  b,  c  で表す（解の公式の実現）
\end{align*}
$$

　「基本対称式を使いながらも、その対称性をうまく破壊して、対称性のない式を作り上げる」ことこそが、解の公式の本質となるわけです。
　もちろん係数 $${a,  b,  c}$$ （と有理数）の加減乗除だけでは、対称式ではない解の公式は実現できません。

　では、どうすればそれが可能となるのか？それが「平方根をとる」という操作です（本シリーズ (22)）。

差積の２乗の平方根を考える

　まず、差積の２乗 $${(\alpha-\beta)^2}$$ を考えます。差積は $${\alpha,  \beta}$$ を入れ替えると変化するので対称式ではありません。

$$
\begin{align*}
\\
\alpha-\beta  &\xrightarrow[入れ替えると]{\alpha  と  \beta  を}  \beta-\alpha=-(\alpha-\beta)\\[8pt]
&\xrightarrow[\hspace{42pt}]{}  {\small 変化するので対称式ではない}
\end{align*}
$$

　しかし、その違いは $${-1}$$ 倍になるだけです。$${-1}$$ は２乗すると $${1}$$ になります。よって差積の２乗は対称式です。

$$
\begin{align*}
(\alpha-\beta)^2  &\xrightarrow[入れ替えると]{\alpha  と  \beta  を}  (\beta-\alpha)^2=(\alpha-\beta)^2\\[8pt]
&\xrightarrow[\hspace{42pt}]{}  {\small 変化しないので対称式である}
\end{align*}
$$

　ここからの計算は、本シリーズ (5) または (22) で詳しくやったのでここでは省略しますが、対称式は、係数 $${a,  b,  c}$$ を用いて表すことができます。実際、次のように表すことができました。

$$
\begin{align*}
\alpha-\beta={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}
\end{align*}
$$

　その平方根をとることによって、プラスとマイナスの値をとりながら、次のように差積を決定することができます。

$$
\begin{align*}
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{align*}
$$

　すると、解の公式を求めることは、次の連立方程式を解くことに帰着させることができます。

$$
\begin{align*}
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\[10pt]
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{cases}
\end{align*}
$$

　この連立方程式を解くと、以下のように $${\alpha,  \beta}$$ が求まります。

(case1)

$$
\begin{align*}
\begin{cases}
\alpha=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[10pt]
\beta=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
\end{align*}
$$

(case2)

$$
\begin{align*}
\begin{cases}
\alpha=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[10pt]
\beta=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
\end{align*}
$$　

　(case1) と (case2) では、プラスとマイナスが入れ替わっているだけです。この結果を一つにまとめることで

$$
\begin{align*}
x=\dfrac{-\dfrac{b}{a}\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

と、２次方程式の解の公式を得ることができます。さらにこれを計算していけば、教科書でも馴染みのある

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

と解の公式が得られます（本シリーズ (18)）。

プラスマイナスの不定性を利用すること

　平方根をとると、必然的にプラスマイナスが伴います。解の公式は、この平方根をとることによって生じるプラスマイナスの不定性（プラスかマイナスかどちらかに限定できない性質）を利用しています（注２）。プラスとマイナスの入れ替えを、２つの解 $${\alpha,  \beta}$$ の入れ替えに対応させているのです。
　具体的に言うと、先の (case1) の解について、プラスとマイナスの入れ替えは、$${\alpha}$$ と $${\beta}$$ の入れ替えに対応しています。

$$
\begin{align*}
&\alpha=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
\alpha,  \beta  の入れ替え\hspace{2pt}&\hspace{-1.5pt}\updownarrow\hspace{6.5pt}\xleftrightarrow[対応]{}\hspace{6.5pt}\updownarrow\pm の入れ替え\\
&\beta=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

　(case2) についても同様に、プラスとマイナスの入れ替えは、$${\alpha}$$ と $${\beta}$$ の入れ替えに対応しています。

$$
\begin{align*}
&\alpha=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
\alpha,  \beta  の入れ替え\hspace{2pt}&\hspace{-1.5pt}\updownarrow\hspace{6.5pt}\xleftrightarrow[対応]{}\hspace{6.5pt}\updownarrow\pm の入れ替え\\
&\beta=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

　つまり、$${(\alpha-\beta)^2}$$ の平方根をとることによって必然的にプラスマイナスは生じますが、そのプラスとマイナスの入れ替えが、$${\alpha}$$ と $${\beta}$$ の入れ替えと一対一に対応しています。プラスマイナスの不定性（プラスかマイナスか限定できない性質）を、$${\alpha,  \beta}$$ の不定性（$${\alpha}$$ か $${\beta}$$ か限定できない性質）へと対応させているのです。

$$
\begin{align*}
\\
プラス &\xleftrightarrow[]{入れ替え} マイナス\\[2pt]
&\hspace{16pt}\updownarrow  {\small 対応}\\[5pt]
\alpha  &\xleftrightarrow[]{入れ替え}  \beta
\end{align*}
$$

　差積の２乗 $${{(\alpha-\beta)}^2}$$ は対称式なので、２次方程式の係数 $${a,  b,  c}$$ の加減乗除で表すことができます。一方、連立方程式のもととなる差積 $${\alpha-\beta}$$ は対称式ではありません。
　そこで、$${{(\alpha-\beta)}^2}$$ の平方根をとることによって、その対称性を破壊します。破棄することで、対称性の壊れた差積 $${\alpha-\beta}$$ を決定することができます。

$$
\begin{align*}
&\begin{cases}
\alpha+\beta=-\dfrac{b}{a}{\small（解と係数の関係）}\\[10pt]
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}{\small（対称式ではない）}
\end{cases}\\[30pt]
&\hspace{18pt}\uparrow  {\small 対称性の破壊}\\[5pt]
&\hspace{8pt}(\alpha-\beta)^2={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}  {\small（対称式）}
\end{align*}
$$

　すると、平方根をとることによって必然的にプラスマイナスが生じます。そのプラスマイナスの不定性を逆用することで、２次方程式の解の公式が実現できる仕組みになっています。
　以上の議論を２次置換を用いてまとめます。まず２次置換の復習です（本シリーズ (19)）。

（復習）２次置換について

　２次方程式 $${ax^2+bx+c=0}$$ の２つの解 $${\alpha,  \beta}$$ について、この２次置換は、次の (case1) と (case2) の２通りがあります。

(case1)　$${\dbinom{\alpha       \beta}{\alpha       \beta}}$$

(case2)　$${\dbinom{\alpha       \beta}{\beta       \alpha}}$$

　それぞれについて詳しくみていきます。

(case1)　$${\dbinom{\alpha         \beta}{\alpha         \beta}}$$ について
　これは $${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に置き換える、つまり何も変化しない置換です。上から下へ変換すると読みます。
　この何も変化させない置換を恒等置換といいます。恒等置換は $${I}$$ という記号を用いて、次のように表記されます。
　$${\dbinom{\alpha         \beta}{\alpha         \beta}=I}$$

(case2)　$${\dbinom{\alpha         \beta}{\beta         \alpha}}$$ について
　これは $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換です。これも上から下へ変換すると読みます。
　これは $${\alpha}$$ と $${\beta}$$ の入れ替えで、そのような置換を互換といいます。互換は $${(\alpha       \beta)}$$ と表記されます。
　$${\dbinom{\alpha         \beta}{\beta         \alpha}=(\alpha       \beta)}$$

（まとめ）２次置換による対応関係

　先の連立方程式を２次置換で説明すると次のようになります。
　$${(\alpha-\beta)^2}$$ は対称式なので、２次置換（恒等置換 $${I}$$ と互換 $${(\alpha     \beta)}$$）で変化しません。
　一方、$${\alpha-\beta}$$ は対称式ではないので、式を変化させない置換は恒等置換 $${I}$$ のみに絞られます。平方根をとることによって、式の対称性（式を変化させない置換）が２次置換から恒等置換に破壊されています。

$$
\begin{align*}
&\begin{cases}
\alpha+\beta=-\dfrac{b}{a}{\small（２次置換で変化しない）}\\[10pt]
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}{\small（恒等置換  I  のみで変化しない）}
\end{cases}\\[30pt]
&\hspace{18pt}\uparrow  {\small 対称性の破壊}\\[5pt]
&\hspace{8pt}(\alpha-\beta)^2={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}  {\small（２次置換で変化しない）}
\end{align*}
$$

　この連立方程式を解くことによって $${\alpha,  \beta}$$ が得られますが、$${\alpha,  \beta}$$ は対称式ではないので、対称性を保つ置換（式を変化させない置換）は恒等置換 $${I}$$ のみです。
　一方、互換 $${(\alpha       \beta)}$$ では、$${\alpha}$$ は $${\beta}$$ に、$${\beta}$$ は $${\alpha}$$ に変化します。その互換 $${(\alpha       \beta)}$$ はプラスとマイナスの交換に対応しています。
　以下 $${\alpha}$$ の方をプラス、$${\beta}$$ の方をマイナスとすると、２次置換の対応関係は

　教科書で馴染みのある形になおすと、対応関係は

　解の公式は対称性が完全に壊れた式です。置換の言葉を使えば、変化させない置換は恒等置換のみとなる式です。
　それを対称式のもととなる係数で表すには、「平方根をとる」という操作を行います。平方根をとることによって必然的に生じるプラスとマイナスの入れ替えを、$${\alpha}$$ と $${\beta}$$ の入れ替え（互換 $${(\alpha     \beta)}$$ の操作）に１対１で対応させることによって、２次方程式の解の公式を実現させています。

（注１）係数の加減乗除で表されるすべての式の集合と、すべての対称式の集合は等しくなること

　本シリーズ (19) でもやりましたが、もう一度簡単に解説すれば、２次方程式 $${ax^2+bx+c=0}$$（簡単のため係数 $${a,  b,  c}$$ は有理数）の解を $${\alpha,  \beta}$$ としたときの＜解と係数の関係＞

$$
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\[10pt]
\alpha\beta=\dfrac{c}{a}
\end{cases}
$$

より

$$
\begin{cases}
\dfrac{b}{a}=-(\alpha+\beta)\\[10pt]
\dfrac{c}{a}=\alpha\beta
\end{cases}
$$

　両辺に $${a}$$ をかけて

$$
\begin{cases}
b=-(\alpha+\beta)a\\
c=\alpha\beta a
\end{cases}
$$

　これより、２次方程式の係数 $${a,  b,  c}$$ は基本対称式 $${\alpha+\beta,  \alpha\beta}$$（と有理数）で表されることが分かります。いわば、係数は対称式の材料です。

$$
\begin{cases}
a  は有理数\\[5pt]
b=-(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})a\\[15pt]
c=\hspace{-12pt}\underbrace{\alpha\beta}_{基本対称式}\hspace{-10pt} a\hspace{28pt}
\end{cases}
$$

　そこで、例えば係数の式として $${a+b+c}$$ を考えると、これに先ほどの $${b,  c}$$ を代入して

$$
\begin{align*}
a+b+c&=a-(\alpha+\beta)a+\alpha\beta a\\
&=a\{-(\alpha+\beta)+\alpha\beta\}\\
\end{align*}
$$

となりますが、この式は $${\alpha}$$ と $${\beta}$$ を入れ替えても式は変化しないので対称式です。 なお、$${a}$$ は有理数の定数なので、式の変化には影響しません。

$$
\begin{align*}
a\{-(\alpha+\beta)+\alpha\beta\}  &\xrightarrow[入れ替えると]{\alpha  と  \beta  を}  a\{-(\beta+\alpha)+\beta\alpha\}\\[5pt]
&\hspace{45pt}=a\{-(\alpha+\beta)+\alpha\beta\}\\[5pt]
&\xrightarrow[\hspace{42pt}]{}  {\small 変化しないので対称式である}
\end{align*}
$$

　一般に、係数 $${a,  b,  c}$$（と有理数）の加減乗除で表される式は、すべて対称式となります。基本対称式の部分は入れ替えても変化しないので、式全体としても対称式となります。
　逆に、例えば $${{(\alpha-\beta)}^2}$$ のような対称式を考えると

$$
\begin{align*}
{(\alpha-\beta)}^2&=\alpha^2-2\alpha\beta+\beta^2\\
&=\underline{\alpha^2+\beta^2}-2\alpha\beta\\
&=\underline{{(\alpha+\beta)}^2-2\alpha\beta}-2\alpha\beta\\
&={(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})}^2-4\hspace{-11pt}\underbrace{\alpha\beta}_{基本対称式}
\end{align*}
$$

　これに＜解と係数の関係＞

$$
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\[10pt]
\alpha-\beta=\dfrac{c}{a}
\end{cases}
$$

を代入すると

$$
\begin{align*}
{(\alpha-\beta)}^2&={(\alpha+\beta)}^2-4\alpha\beta\\
&={\left(-\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}\\
&={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}
\end{align*}
$$

となり、係数 $${a,  b,  c}$$（と有理数）の加減乗除で表すことができます。
　一般に、すべての対称式は係数 $${a,  b,  c}$$（と有理数）の加減乗除で表すことができます。＜対称式の基本定理＞より、すべての対称式は基本対称式 $${\alpha+\beta,  \alpha\beta}$$ の加減乗除で表すことができ、それに＜解と係数の関係＞を代入することで、係数 $${a,  b,  c}$$（と有理数）の加減乗除で表すことができます。
　以上より、＜解と係数の関係＞を仲介させることで、集合 $${Q_2}$$ と対称式の集合は等しくなることが分かります。

（注２）平方根をとることによって生じるプラスマイナスの不定性

　例えば $${x^2=3}$$ の解を考えます。この解は、両辺の平方根をとって

$$
\begin{align*}
x=\pm\sqrt{3}
\end{align*}
$$

となりますが、$${x=\sqrt{3}}$$ か $${x=-\sqrt{3}}$$ か、どちらかに限定することはできません。必ずプラスとマイナスの両方の解が現れます。それが「平方根をとることによって必然的に生じるプラスマイナスの不定性」という性質です。
　もちろん、$${x>0}$$ という条件があれば $${x=\sqrt{3}}$$ と限定されますが、なにも条件が無い場合は、必ずプラスとマイナスが伴います。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となることを解説
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）「対称式ではない解の公式を基本対称式で表す」という課題を、平方根をとることによって必然的に生じるプラスマイナスの不定性によって克服すること。