
【夢のある乗数効果の凄味、財政政策】マクロ経済学part5
先日、日本のGDPがドイツに抜かれてしまいましたね。GDPに関心を持つ方も少なくはないでしょう。そんなあなたに100年前ほどに作られたGDPを増やす考え方を伝授します!!
どうもこんにちは! こちらの続きです!
前回のあらすじ
マクロ経済学はグラフを動かして、GDP(財・サービスの総量)を上げることを目標にする。
分配=生産=支出の関係を三面等価の原則という
財市場での均衡(人々が満足すること)する関係式は$${\left\{ \, \begin{aligned} & Y_d=cY+C_0+I+G \\ & Y_d=Y \end{aligned} \right.}$$
GDPを増やそう
もしもグラフが動いたら。。。
もしも傾きが緩いほう($${Y_d=cY+C_0+I+G}$$)が上に動いたら、均衡点すなわち国民の満足具合はどうなるでしょう。

満足いくGDPが増えましたね。これが初回から常々説明している、「グラフを動かしてGDPを増やす」ということです。
グラフを動かす手段
さて、問題はグラフの動かし方です。動かすグラフは$${Y_d=cY+C_0+I+G }$$の方です。$${Y_d=Y}$$のほうは動きません。総需要と実際のGDPの関係は同じという前提で話が進んでいるので、$${Y_d}$$もしくは$${Y}$$が一方的に増えるというわけではございません。
$${Y_d=cY+C_0+I+G }$$のグラフを上に動かすとして、どう動かすかを考えてみましょう。右辺の方が増加すればグラフは動きます。

右辺が増加するには、$${cY, C_0 ,I ,G }$$の4つの項目のうちどれかを増加すればよいと考えられます。
(ただし、消費関数:$${C=cY+C_0}$$が増加するには、GDPが上がるか、基礎消費が上がるかの2択です。前者はそもそも我々の課題(GDPをグラフを使ってあげる)なのでどうにもなりません。所得に関係ない基礎消費量を上げるのは難しいので、後者を意図的に上げるのは厳しいでしょう。投資:$${I}$$についても同様に、企業が設備投資を増やす動機付けをするのは難しいでしょう。)
そこで、右辺を増加させるには政府の財政出動により、政府支出$${G}$$を増やすという流れが考えられます。
政府が公共、公的サービスにお金を使うことが、$${Y_d=cY+C_0+I+G }$$の右辺を上げることに繋がるのです。
このことを財政政策と呼びます。
Gを増やすとどうなるのか
そこで$${G}$$を増加させていきます。先程の例では、【需要の増加分】と称しましたが、数学的に記号を使わせてください。
$${\Delta G}$$を政府支出の増加量とします。$${\Delta}$$:デルタと読みます。意味は増加分という意味です。「+ちょこっと」みたいに捉えましょ~。

縦軸に注目、$${\Delta G}$$の分増やしました。横軸に注目!$${Y}$$もその分増えます。$${\Delta Y}$$をGDPの増加量とします。
財政政策による夢のある乗数効果
ここで、縦軸と横軸の増え方に注目してください。なんか$${\Delta G}$$以上に$${Y}$$が増えますよね。
このように政府支出量よりもGDPが増える現象を乗数効果といいます。わりと夢がありますよね。例えばですが、公共サービスに10億円支出するとしたら、GDPが30億円ほど増えるようなイメージです。(10億とか30億とかはたとえ話なので真に受けないように)
この乗数効果の仕組みは難しいので教養程度に読んでる方は飛ばしてもらっても構いません。仕組みを解説します。
乗数効果の仕組み
結論を申し上げます。$${\Delta Y=\frac{1}{1-c}\Delta G}$$となり、$${\frac{1}{1-c}}$$の分増えます。なので、$${c}$$(限界消費性向)が75%ならば、$${\frac{1}{1-0.75}=4}$$となり、4倍に増えます。80%ならば、5倍に増えます。家計の消費する率によって、政府支出の何倍ものGDPが増えます。まさに夢でしかありません。
$${\frac{1}{1-c}}$$を乗数と言ったりします。
なぜこうなるのか2通りで解説します。長いので飛ばしてしまっても構いません
まずは数式から。字体を少し変えます。
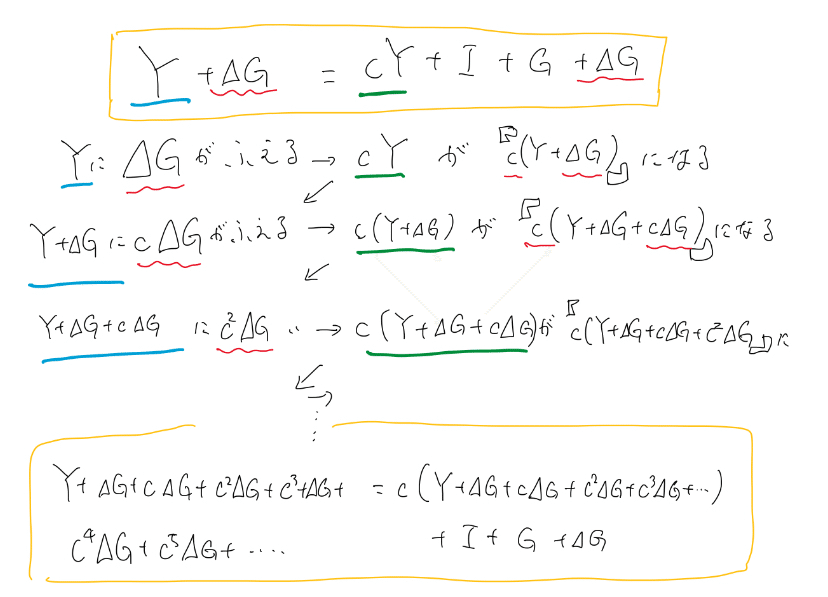
$${Y=cY+I+Gが\Delta Gだけ増えると、左辺Yも増えます。\\ Y+\Delta G= cY+I+G+\Delta G\\\,\\この際、Yが(Y+\Delta G)となるので右辺Yも増えます。\\Y+\Delta G< c(Y+\Delta G)+I+G+\Delta Gとなり、右辺はc\Delta G増えました。\\c\Delta Gだけ増えると、左辺Yも増えます。\\ Y+\Delta G+c\Delta G= c(Y+\Delta G)+I+G+\Delta G\\\,\\この際、(Y+\Delta G)が(Y+\Delta G+c\Delta G)となるので右辺(Y+\Delta G)も増えます。\\Y+\Delta G+c\Delta G< c(Y+\Delta G+c\Delta G)+I+G+\Delta Gとなり、右辺はc^2\Delta G増えました。\\c^2\Delta Gだけ増えると、左辺Yも増えます。\\ Y+\Delta G+c\Delta G+c^2\Delta G= c(Y+\Delta G+c\Delta G)+I+G+\Delta G\\\,\\この際・・・と無限に続くと、\\Y+(\Delta G+c\Delta G・・・c^n\Delta G+・・・)\\= c(Y+\Delta G+c\Delta G+・・・c^n\Delta G+・・・)+I+G+\Delta G\\となります。\\\Delta G+c\Delta G+・・・c^n\Delta G+・・・の部分を\Delta Yとすると\\Y+\Delta Y=c(Y+\Delta Y)+I+G+\Delta Gとなり\\両辺Y=cY+I+Gを引くと\\\Delta Y=c\Delta Y+\Delta Gよって\Delta Y=\frac{1}{1-c}\Delta G}$$
2つ目はグラフを使います。

①:【横に注目】$${Y_d}$$に、縦に$${\Delta G}$$増やすと、同じ量だけ横にも$${\Delta G}$$増えます。
②:【縦に注目】横に$${\Delta G}$$増えると、縦に$${c×\Delta G}$$だけ増加。
③:【横に注目】縦に$${c×\Delta G}$$増やすと、同じ量だけ横にも$${c×\Delta G}$$が増える。
以下、①と②のような流れをループする。
すると、$${\Delta G+c\Delta G+c^2\Delta G+・・・+c^n\Delta G+・・・}$$と増え、無限等比級数の和より$${\frac{1}{1-c}}$$が得られる。

さらっと無限等比級数の和を使いましたが、$${\Delta G+c\Delta G+c^2\Delta G+・・・+c^n\Delta G+・・・}$$を計算しただけです。
GDPは上がったけど。。。
このシリーズの目的である、GDPをグラフを使ってあげるという試みは達成しました。ですが、マクロ経済学はここでは終わりません。GDPが上がると、需要が下がるものがあるのです。需要が下がるとなると、$${\Delta G}$$が増えたら、その何倍ものGDPが上がるというわけではないことになってしまいます。
乗数効果が3倍としましょう。10億の公共支出をしたら、30億のGDPが増えますが、そこから何らかの理由で5億円ほどGDPが下がってしまうみたいなイメージです。
その正体は金融市場という新ステージにあります!ここから新しい章の幕開けとしてみていきましょう!
まとめ
財政政策により、政府が支出をすることで、GDPが政府支出以上に増加することを扱いました。まあ、あくまでただの理論なので現実に必ず適応できるとは限らないですけどね~。ただ、このようにグラフでGDPを上げる考え方を知っておくのは教養としても大事ではないでしょうか。私もこの考え方は結構好きです。醍醐味だと思います。
そして、金融市場がGDPと何か関係があるのでそこについて探っていきたいと思います。
次回はこちらから!
