
平方根が感覚的・直観的にわかるコツは平方数
こちらの記事
https://note.com/shihohashi/n/n7de509eda9ab
では、平方根の概念を直線的に捉えてみました。
まとめてみますと、こういう概要でした。
ある数を境に、
左方向矢印では平方根で一旦小さくした数を、二乗にして元の数の戻す、
右方向矢印では一旦二乗に拡大した数を、平方根で元の数に戻す。
これは、平方根を直線的に捉えている、とどのつまり、1次元で平方根をキャッチしたことになります。
点よりも線、線よりも麺ではなく面、面よりも立体のほうが感覚的にうったえるものがあるように、平方根だって少し次元を高めた方が感覚的に理解しやすいと思ったので、今回は、二次元で平方根を捉えよう!というお話を書いていきたいと思いmath
そして、前回の記事では、整数も平方根になりますねって話(はなぴ)でした🎵
平方数とは?
平方数は何かの数字の二乗で表されている数です。3^2とか2^2とかn^2とかです。
平方根とは?
「ある数を二乗したらその数になるような数」
初耳の時には何これ珍百景?状態でした。どの数?みたいな。
そう思われた方は、こちらの記事を読んで、直線的、流動的になるほどとなってもらえればと思いまPた。概要を感覚的にキャッチできると思います。
https://note.com/shihohashi/n/n7de509eda9ab
で、更に今回は二次元で平方根捉えたら、さらにイメージしやすいだろうということ煮て焼いて、あ、でもこれって、幾何学的な捉え方なんですね!ということで、正方形で考えていきませう。
平方は正方形
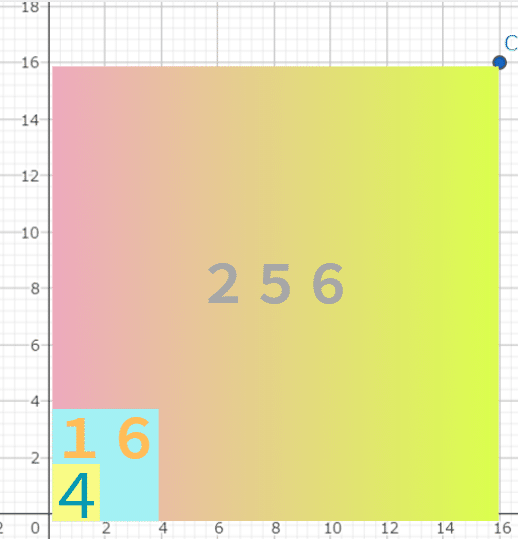
面積が16(単位省略しております)の正方形の一辺は4(単位省略しております)ですね。
一方、16を一辺とする面積は256ですね。
4×4=16→16→16×16=256→256→256×256=?
2×2=4→4→4×4=16→16→16×16=256→256→256×256=?
図で表すとこうなりました。
ここで気になったのは、平方数と平方根、どちらも平方が付いています。平方を考えた時、ヘイヘイホー🎵のループしましたが、平方とは、
自乗(じじょう)とは、ある数を自らと掛ける演算、あるいは演算によって得られる数を指す。
二乗(にじょう)、平方(へいほう、英: square)[1]とも呼ばれる。

Xの数値×Xの数値=y、yは正方形を表しているよってことですね。たしかに、xが10の時、面積100ですね。
なるほど、平方というのは二乗のことでさらに、squre:正方形とも呼ばれていたんですね!
ある数を平方根する⇔ある数を二乗する
今回は平方根を感覚的、直観的にとらえやすくするということでした。
平方を元に考えますと、正方形の面積aがあります。
・aを平方(二乗)すると→a^2という面積になります。
→一辺が4の直線を二乗すると16の面積となります。
ここまでは普段からよく使っています。
問題は、ある数を平方根にするって?ってことです。
面積で考えてみますと、
面積から一辺を求めることが、ある数の平方根を求めるってことになります。
具体的には、
面積→平方根する→面積の数値に√つける→√面積→面積が平方根できた!
というわけで、ある数の平方根をつくることを、ある数を二乗する、平方するという使い方と同様に、「ある数を平方根する」と考えます!
・ある数を二乗する→ある数に「^2」つける。
→4を二乗する→4^2
・ある数を平方根する→ある数に「√」つける。
→16を平方根する→+-√16=+-√4^2=+-4
ある数を面積と見立てた時、その1辺を求めるには、面積と見立てた数に√をつければいいということですね!
で、
その数に√をつける操作を「平方根する」って言えば簡単に、ある数の平方根を求められますね。
例えば、面積16の場合、16を平方根すれば+-√16=+-4で、面積の1辺は正の値なので4となるわけですね。
ここで、平方根した数が元の数16であり、平方根された数が正方形の1辺の数となります。
そして、平方根された数には性質があるんだと。
平方根された数を平方すると、元の数になる!
こうやって覚えておくと簡単
。
平方平方元の数。→平方根した数を平方(二乗)すれば元の数でしょ。
もし、平方平方元の数で、最初の平方は平方根だっけ?平方だっけ?となってしまった場合は、大根を思い浮かべてください。そうすれば、最初の数は、新種の野菜、平方根だと気付くでしょう。
これに慣れてくれば、あとは、元の数を16と考えて(理由は特にありません、キャパの問題かも。あんまし大きな数だとパッと浮かばないから?というわけで、お好きな数で唱えてみてください)。
練習問題:この問題では、問題を思い浮かべて自由自在に作ることが目標です。
・元の数平方で平方根
→+-√16
・平方根の平方が元の数
→(+-√16)^2=16
・元の数の平方は面積
→16^2=256
・元の数を平方した面積を平方根すれば元の数
→16^2=256→+-√256=+-√16^2=+-16
・平方根した数を平方した数は平方根した数を1辺とする正方形の面積
→16start→平方根する→+-√16=+-√4^2=+-4(平方根された数)→+4^2(1辺の二乗)=16(面積)
・元の数は平方根を1辺とする正方形の面積
→16=√16×√16
などなど色々変化を楽しめますね。
今まで、1辺が分かってから、正方形の面積を求めていましたが、正方形の面積を設定してから、1辺を簡単に求めることが、平方根によって実現できるんだと。
絶対値に注意_平方根する場合は+-の二種類が必要
「平方根する」ということは、「二乗したらその数になる」数をつくるということです。
なので、「二乗したらその数になる数」について、4も-4もどちらも二乗すれば16になります。
なので、16というある数を平方数にする場合は、ある数は既に絶対値+なので、平方数にする場合も、16^2=256と絶対値+のままです。
一方、二乗して16を作る場合は、2通りあるってことですね。なので、+-√16というように、「平方根する」つまり「ある数に√を付ける」場合は、絶対値は+と-の2種類つけ麺でなく、付けるんですね!!
というわけで、平方からわかる平方根の話で、更に平方数を使えば、正方形から1辺がすぐに、平方根によって求まるって話でPた。
今日の一句
明日の分も作り置き
