【デスペ6問】関数従属性の集合表現（データベーススペシャリスト）
このNoteには、関数従属性の集合表記を集めました。
関数従属はとにかく「大元」となる要素を特定することです。
要素同士の従属性を→で図示すると、理解が捗ります。
このNoteは、データベーススペシャリスト独学合格、IT専門学校の先生の経験を基に書いています。
それでは始めましょう！
候補キーを答える問題
まずは「大元」を探す問題からいきましょう。
正規化でいえば、主キー（の候補）探しです。
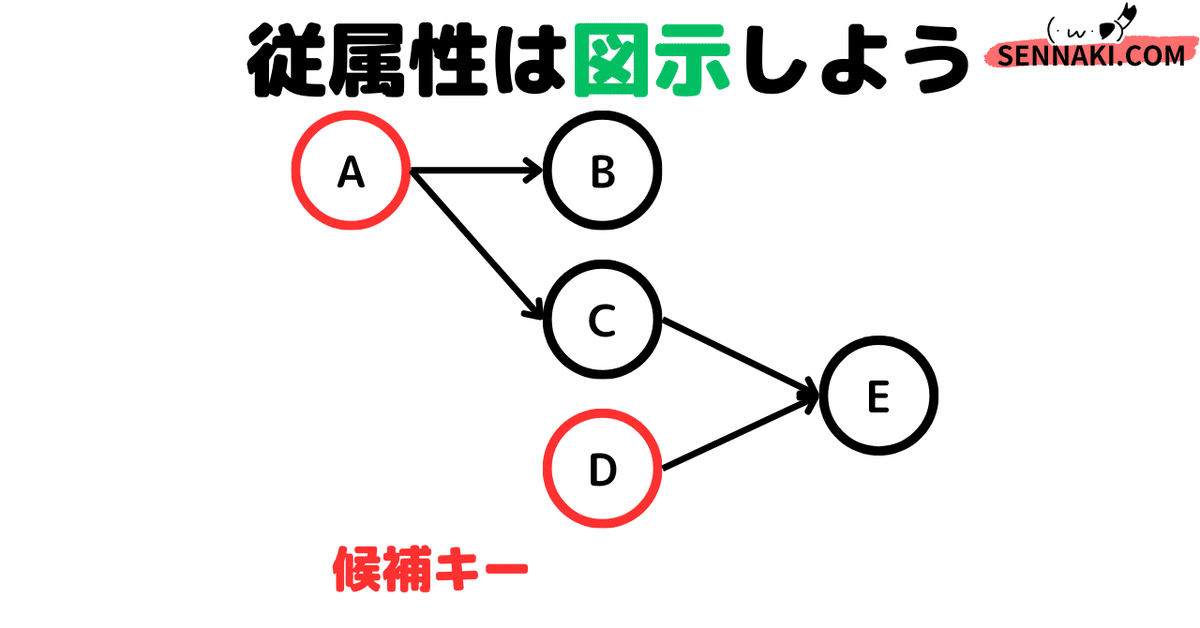
スキーマが{A, B, C, D, E}で、関数従属性がA→B, A→C, {C, D}→Eである。属性集合{A, B}を与え、関数従属性から導出される属性を属性集合に加える操作を繰り返し、最終的に得られる属性集合の閉包はどれか
ア：{A, B, C}
イ：{A, B, C, D}
ウ：{A, B, C, D, E}
エ：{A, B, E}
令和04年午前2問03より改変
正答はア。
{A, B}が与えられれば、A→B, A→Cによって、Cが決まります。
確認のためにDやEが決まるかを確認します。
Dを決める従属性の記載はなかったです。Eを決めるには{C, D}が必要ですが、Dが与えられないので求められません。
スキーマが{A, B, C, D, E}で、関数従属がA→{B, C}, {C, D}→Eである。候補キーはどれか。
ア：{A, C}
イ：{A, C, D}
ウ：{A, D}
エ：{C, D}
平成30年午前2問3より改変
令和02年午前2問3より改変
正答はウ。
A→{B, C}よりAが候補キー
{C, D}→Eにおいて、CはAから求まりますが、Dが求まらないため、Dが候補キー
以上より、ウ｛A, D｝が候補キー。
スキーマ{A, B, C}で関数従属A→B, B→Cがあるとき、導けない関数従属はどれか
ア：{A, B, C}→{A, B}
イ：{A, C}→{A, B}
ウ：{A, C}→{A, B, C}
エ：{B, C}→{A, C}
正答はエ。
ア：問題なし。A,Bが与えられればA,Bが求まるため。
イ：問題なし。Bは、問題文よりA→Bで求まります。
ウ：問題なし。Bは、問題文よりA→Bで求まります。
エ：問題あり。Aを求める術ががありません。もし問題文に「何か→A」があれば求まりましたが。
集合論の問題
意識はしないですが、例えば掛け算にも法則があります。
交換法則：2 × 3 = 3 × 2
結合法則：(2 × 3) × 4 = 2 × ( 3 × 4)
分配法則：2 × (3 + 4) = 2 × 3 + 2 × 4
集合にも同じように、反射率・増加律・推移律・合併律・分解律など、法則（特性）があるのです。
とはいえ、覚えると大変。私たちは数学者を目指しているわけではないですからね。
「考える」で対応しましょう。
スキーマの属性A, B, Cの関係従属について正しい記述はどれか。
ア：A→Bで、A→Cならば、B→Cである
イ：BがAの部分集合で、A→Cならば、B→Cである
ウ：BがAの部分集合ならば、B→Aである
エ：BとCの和集合がAに関数従属するならば、A→B, A→Cである
正答はエ。
ア：A→{A, C}ですが、B→Cの記載はありません。
イ：BがAの一部なので、B→一部のCですが、C全体を決められません。
ウ：BがAの一部分なので、A→Bです。
エ：正しい。Aから、和集合（BまたはC）が求まるので。
数学的な図解については「過去問道場さん」を見てくださいね。
難しい問題
AMIIには複雑な関数従属性が出て、なかなか一発で解けない場合もあり、選択肢から絞り込むテクニックを用いることもあります。
しかし、データベーススペシャリストでは「正規化できるぐらいの関数従属性の理解」があれば充分。ひとまず「AMIIで正解が引ければOK」と考えてください。
ここに載せた2問は、少しモヤっとしますが、その程度の理解でデスペ的には充分。正規化の問題、午後問題には充分な理解です。
スキーマが{A, B, C, D, E}で、関数従属が{A, B}→C, {B, C}→D, D→{A, E}である。候補キーはどれか。
ア：{A, B, C}
イ：{A, B}, {B, C}
ウ：{A, B}, {B, C}, {B, D},
エ：{B, C}, {C, D}
正答はウ。
{A, B}→Cより、{A, B}を候補キーになる線で考えてみます。
{A, B}→Cより、AとBが候補キーになりそう。
{B,C}→Dは、Cは上記でA,Bから決まるため、Bのみ候補キーになりそう。
D→{A, E}より、Dは上記でB, Cから決まるため候補キーにはならなそう。
以上より、{A, B}が候補キーなら、C, D, Eが求まりそうです。
ただし、D→{A, E}なので、Aが候補キーでない場合もありそうです。
{B, C}→Dより、{B, D}を候補キーにする線で考えてみます。
{B, C}→Dは問題なし。Dが新たに求まります。
D→{A, E}は問題なし。AとEが新たに求まります。
{A, B}→Cについて。そもそもCは{B, C}で与えられているので問題なし。
以上より、{B, C}が候補キーでも、D, A, Eが求まりそうです。
D→{A, E}より、Dを候補キーにする線で考えてみます。
D→{A, E}より、AとEが求まります。
{A, B}→Cについて、Bが必要そうです。
{B, C}→Dについて、Cは上記で求まりますが、Bは必要そうです。
以上より、DのみではA, Eは求まりますが、Bが必要そうです。よって候補キーは{B, D}。
以上より、候補キーは{A, B}, {B, C}, {B, D}の3パターンが考えられます。
従属性は図示しても分かりやすいので「過去問道場さん」も覗いてみてくださいね。
スキーマ{A, B, C, D, E}について、集合W={A→{B, C}, {A, D}→E, {A, C, D}→E, B→C, C→B}がある。次の集合X, Y, Zのうち、Wから冗長な関数従属をなくしたものはどれか。
X={A→B, B→C, C→B, {A, D}→E}
Y={A→C, B→C, C→B, {A, D}→E}
Z={A→B, C→B, {A, C, D}→E}
ア：Xのみ
イ：XとY
ウ：YとZ
エ：Zのみ
正答はイ。
W={A→{B, C}, {A, D}→E, {A, C, D}→E, B→C, C→B} から従属性を挙げてみます。
A→{B, C}
{A, D}→E
{A, C, D}→E
B→C
C→B
この中で「→A」の形だけないので、A始点で考えてみます。
A→{B, C}：問題なし
{A, D}→E：他にDを求める術がないため問題なし。
{A, C, D}→E：CはAから求まるので不要、Dを求める術がないため問題なし。{A, D}→Eで充分。
B→C：CをBから求めなくても、A→{B, C}でAから求まる。
C→B：BをCから求めなくても、A→{B, C}でAから求まる。
以上より、{A, D}があれば他は求まりそうです。
{A, C, D}→Eは不要なので、Zは不要となり、選択肢はアとイに絞れます。
XとYの片方だけで良いのか、両方なのかを考えます。
X={A→B, B→C, C→B, {A, D}→E}
Y={A→C, B→C, C→B, {A, D}→E}
A→{B, C}から、A→BかA→Cの片方を残しています。
CやBはB→CかC→Bで決まり、BやCはAから決めるしかありません。よってXとYの2パターンともOK。どちらかが間違い、ではなかったです。
よって正答はイ「XとY」。
p.s. 普段は >> 専門学校とIT就職のブログ << をやってます。
でわでわ（・ω・▼）ノシ
この記事が参加している募集
学習方法・問題特集のNoteは全て無料提供を続けます▼ もしご覧になったNoteが有益だったり、私の志に共感されたりしましたら、サポート頂けますと励みになります▼ もちろんコメントでも結構です(・ω・▼)ノシ