コロナの報道を見るときに知っておきたいバイアスのこと　#1

こんにちは　眠らないウサギです
継続的に読んでくださっている方、いつもありがとうございます😊
今回初めて僕の投稿を読んでいただいている方、初めまして😊

初めましての方はよかったらプロフィールや自己紹介を覗いていって頂けると眠らないウサギって何者や？ということは少しお分かりいただけるかもしれません😊

はじめに

さて今回は題名の通り世界的に流行している感染症がありますが、そのニュースを見るにあたって知っておきたいことをバイアスの観点から例題を通して書かせていただこうと思います。

この記事及び執筆者の立ち位置(注意書き的なやつ)

その前に今流行している感染症は少しセンシティブな話題とも言えるのでこの記事及び執筆者の立ち位置を書かせてください。気にならない方は読み飛ばしていただいて構いません。
私はこの記事で自分の感染症に対する主義や主張を述べるつもりは更々ありません。もちろんワクチンについても然りです。様々な考えがあって当然でそれぞれ尊重されるべきであると考えております　バイアスの観点から紹介する中でこれは批判しているのでは？とお思いになられる方もいらっしゃるかもしれませんが、あくまでも私はここでは中立の立場からこういうバイアスが存在するという事実を紹介するまでとします。記事を読んでの感想、批判、疑問などコメントやDMにくださるのは大歓迎ですが、念のため私の立場を御理解したうえで意見を頂戴ください😊

導入

さて、早速本題に入りたいのですがまず今回は基準率錯誤についてです。
古参の方はおいおい、こいつまたやりよったと思うかもしれません（笑）
最初はわざと知らなそうな単語で気を引いてという例の”悪徳商法”です😂

さてもう少し詳しくいくと殊、感染症に絡めた話題では偽陽性についての話題です。ここから偽陽性ってなんだ？という話を今回はしようと思います。丁寧にするつもりなので最後まで読んでいって頂けると嬉しいなと思います😊

例題

以下のケースについて考えてみましょう(なお、数字が出てきますが現在流行している感染症とは全く関係ない数字であることにはご留意ください)

1万人に1人の割合で感染する病気があるとします。検査によって陽性/陰性判定が出来ますがその信頼性は99%を誇ります。感染していたら99%の確率で陽性判定が出来、感染してないのに陽性と出るエラー率もわずか1%という優れた検査法であることが知られています。以下の状況において、自分が検査により陽性と告げられた時、どのような判断をするのが統計学的に正しいと言えるでしょうか？

読者の皆さんはどう思いますか？　99%の確度を誇る検査で陽性って出たならヤバいじゃん～😭って感じですか？　いやいや、何を言ってんだい　そんなの恐るるに足らずですな😇って感じですか？

統計学的が分かっていれば、後者のように感じると思います。何が起こっているのかを以下に解説いたします。

解説

結論から言うと陽性と判定されたとしてもあなたが病気である確率は実は1%にも満たない0.98%程度です。え？99%の確度を誇る検査なんちゃうん？と思う方もいらっしゃるかもしれません　そうです　99%の確度を誇る検査でも陽性判定で病気である確率は1%を切っています。

簡単のために全体を100万人としましょう　1万人に1人ですから病気の人の人数は100人です。99%正しい判定を検査はしてくれるので100人のうち99人は正しく陽性判定を受けます。ここまではすんなりでしょう。問題はここからです。病気にかかってない99万9900人について考えてみるとこれらのうち間違って陽性と判定を受けてしまう人は99万9900人のうち1%ですから9999人いることになります。ここがこの問題の肝です。

つまりここまでのことから陽性と判定された人には2種類のタイプがあり、病気で陽性と判定された人が99人、病気でないのに陽性と判定された人が9999人、合わせて10098人が陽性と判定されます。先述の通りこのうち病気なのは99人であり、確率は100×99/10098で0.98%です。この問題のトリック分かっていただけましたでしょうか？　一応表を作ったのでそれを以下に示します。

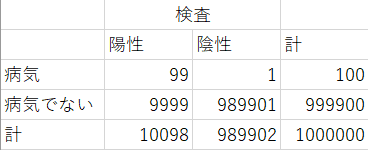
ここまで見れば、なるほど～　この状況下においては99%の確度の検査で陽性と出ても病気である確率は1%未満だし、必要以上に恐れる必要はないなと判断できるかと思います。

問題の考察

偽陽性は、感染していないのに「感染している」と判定されてしまうことです。偽陰性は偽陽性の逆で、感染しているのに検査で「感染していない」と結果が出てしまうことです。偽陽性と偽陰性はトレードオフの関係にあり(こっちをたてるとあっちがたたずって状態のこと)どちらも減少させるというのは出来ないものであります。これは統計学の仮説検定における第1種の過誤、第2種の過誤とほぼ同じものです。（興味ある方は統計学の本などをご参照ください）

トレードオフの場合どうバランスをとるかが大切になります。
偽陽性を決して出さまい！！と息巻いて、感染を抑え込むんだ！！というと聞こえは良いですが、裏では感染していないのに陽性判定を食らう人が増えることになります。
一方、感染してないのに陽性判定を食らうのは社会的に損失が大きいし、かわいそうと思っていると、感染してる人を陰性と判断するケースが増えてしまい、一向に感染は収まらない可能性が高くなります。

このことは何も今般の感染症に限った話ではありません。企業における不良品のチェックなどにも同じことが言えます。

検査というものにはいままで書かせていただいたようなものがつきものである、そして時にそれは直感に対し大きくずれることがあるということが分かれば大きな大きな収穫です。

おわりに

以上が第1回、基準率錯誤についてのお話です。感想などコメントやDMで大歓迎です～！！　どんなコメントでも目を通しますので遠慮なくど～ぞ😊

第1回の反応を見てという風にはしますが、一応このシリーズでもう1回くらいはバイアスについて書こうかなとおもっています。いつ出すか自分でも決めてないので気になる方はフォローしていただけると見逃しづらいかと思いますのでよかったらフォローの方お願いします😊（なんかYouTuberみたい😇）

長々とお付き合いいただきありがとうございました。

それではばいちゃ！

参考文献
https://www.h-cl.org/column/pcr-false-positive/
自分では気づかない、ココロの盲点　池谷裕二　講談社