
周波数分析ってなあに?
デジタル信号処理の基本となるのがどんな波形が含まれていてどんな周波数特性をしているのかを解析する周波数分析である
波形から周波数特性を求めるのに使うのが離散フーリエ変換 (DFT, Discrete Fourrier Transform)で、逆に周波数特性から波形を求めるには逆離散フーリエ変換 (IDFT, Inverse Discrete Fourrier Transform) を使う
x(n)を波形、X(k)を周波数特性、nを時間、kを周波数とすると、離散フーリエ変換と逆離散フーリエ変換は次の式で表される
$${X(k)=\sum_{n=0}^{N-1}x(n)\exp(\frac{-j2πkn}{N}) (0\leq k\leq N-1)}$$
$${x(k)=\sum_{k=0}^{N-1}X(k)\exp(\frac{j2πkn}{N}) (0\leq k\leq N-1)}$$

分析区間を切り取る際にそのまま切り出してもよいが、それだと波形の断面のせいで周波数分析にノイズが入る恐れがある
そこでそのまま切り取るのではなく、例えば両端を絞って切り取る方法が使われる
このような切り取る方法全般を窓関数と言い、前者は方形窓、後者はハニング窓などがある

周波数特性の時間変化を可視化するためのツールをスペクトログラムという
窓関数を少しずつ時間方向にずらしながら周波数分析を繰り返し、横軸に時間、縦軸に周波数特性を濃淡表示したものをいう
例えば1秒ごとに周波数が500Hzずつ高くなっていくサイン波のスペクトログラムは次の通り

木琴の内の2種類であるマリンバとシロフォンの周波数分析をしてみよう
次図はA4の音を鳴らしたときのマリンバの波形と周波数特性を表している
A4の音である440Hzに加えて、4倍音と10倍音が見て取れる

次にシロフォンを見て見ると、3倍音と6.5倍音が見て取れる
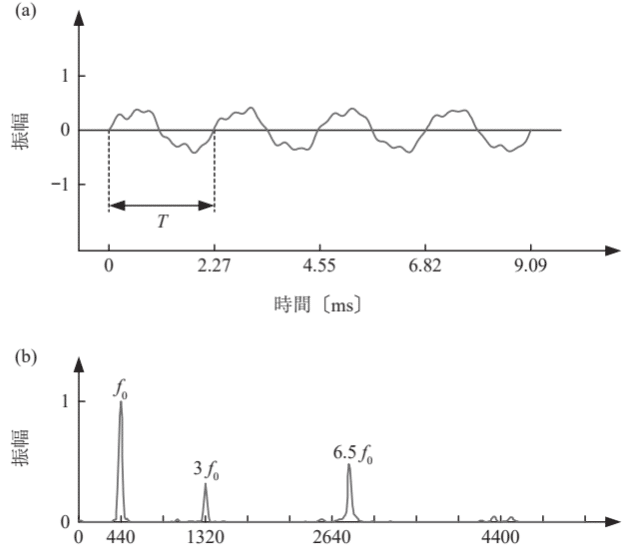
このように音を出す物体というのは特定の振動しやすい周波数(モード周波数)があり、モード周波数の音は大きく聞こえる(共鳴)
逆に言うと、狙った音色を出すために楽器には特定の加工がされるのである
いいなと思ったら応援しよう!

