
三角関数 | 和積の公式を図形を用いて導く方法

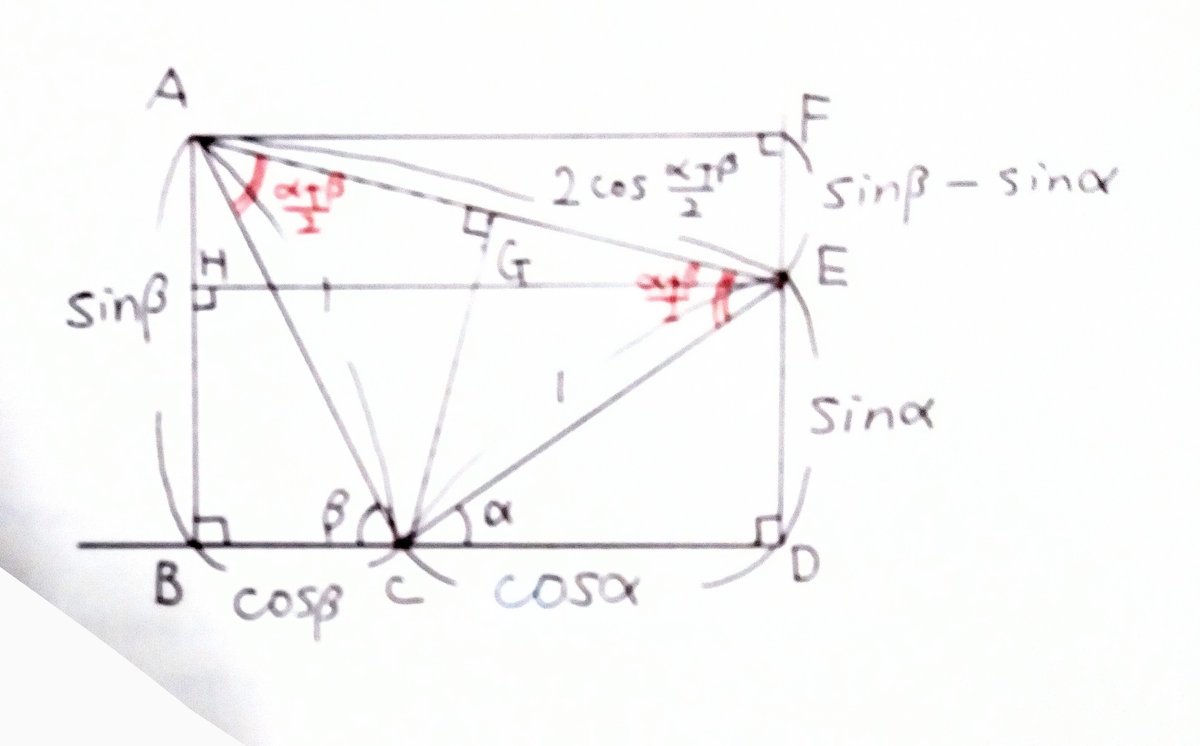
長方形ABDFの辺BD上に、点Cをとる。
AC=CE (=1)となる点Eを辺DF上にとる。
∠DCE=α、∠ACB=β とすると、
CD=cosα、DE=sinα、
BC=cosβ、AB=sinβである。
△ACEにおいて、
∠ACE=180-α-β である。
AC=CE の二等辺三角形だから、
∠CAE=∠CEA (=底角)は等しい。
よって
∠CAE
=∠CEA
={180-(180-α-β)}÷2
=(α+β)/2
もう一度、図を掲載すると、次のようになる。

次に△ACEの頂角∠Cから底辺AEに垂線を下ろしたときの交点を点Gとすると
線分EG=cos{(α+β)/2} 。
また線分EG=線分AGだから
線分AE=2cos{(α+β)/2} 。

次に点Eから線分ABに垂線を下ろし、
交点Hをとる。
平行線の錯角は等しいから
∠DCE=∠CEH=α 。
また、∠CEA=(α+β)/2 だから、
∠AEH=(α+β)/2 - α = (β-α)/2
また、∠AEH=∠EAF (平行線の錯角)。
よって、△AEFは、次のように図示することができる。

よって
cos{(β-α)/2}
=(cosα+cosβ)/2cos{(α+β)/2}
したがって

同じ図から
sinβ-sinα の公式も導くことができる。
加法定理についてはこちら(↓)
いいなと思ったら応援しよう!

