
数学 | そもそも行列って何の意味があるの?
(1) 全部が好きってわけじゃない
数学は好きだが、嫌いな分野も多い。
方程式、微積分、三角関数、図形の問題は難しくても、理解出来ないことがあっても、好きだ。
しかし、確率・統計や線形代数(行列)は理解できることがあっても大嫌い。あまり見たくない。考えたくない。
これって、私だけなのかなぁ、なんて思ったこともあったけど、理系の人でも確率・統計は苦手という人は意外と多いらしい。
まぁ、数学を専門にやる人ならば、確率も線形代数も避けては通れないものだろうが、私は趣味で数学してるだけなので積極的に勉強しようとは思わない。必要に応じて、軽く軽くたまに勉強する程度だ。
(2) 確率と行列が嫌いな理由
確率・統計が嫌いなのは何でかなぁ、なんてろくに勉強もせずに考えることがある。一言でいえば、リアリティを感じにくいことと、必然性を感じないこと。
もともと確率統計って、ギャンブルとか保険屋さんたちに必要とされて発達してきた学問。そういうのって興味がなく、縁遠くて。ギャンブルには全く興味がないし、保険の契約書なんてまともに読もうとしても嫌気がさしてくる。
正規分布を利用しよう!みたいなことを言われましても、そもそも正規分布ってどこから出てきたのよ?って思ってしまって。
それに「それはそういうものなのだよ」みたいなことしか書いていないし。
線形代数( 行列 )が嫌いなのは、そもそも必要性がよくわからなかったから。
高校数学では、二行二列の行列しか学ばなかった。だからかもしれないが、普通に解ける連立方程式を何でわざわざ行列に置き換えて考える必要があるのかと。
大学で、サラスとか三行三列を扱って、表記の面で行列のほうがスッキリ表現できるなぁ、とは思ったが、「絶対必要だ!」とは必ずしも思えなかった。
だから、サラス、ヘッセ行列、ヤコビアンくらいしかいまだに知らない。
とはいえ、行列式もいいかも、と思ったこともある。
以下に書くことは、私が「いいな」と思っただけで、たぶん「なにが?」みたいな話なので、興味がある方だけ読んでいただければうれしい。無理に分かる必要もない。
(3) サラスの公式と行列式を使って
①サラスの公式をそのまま使う。
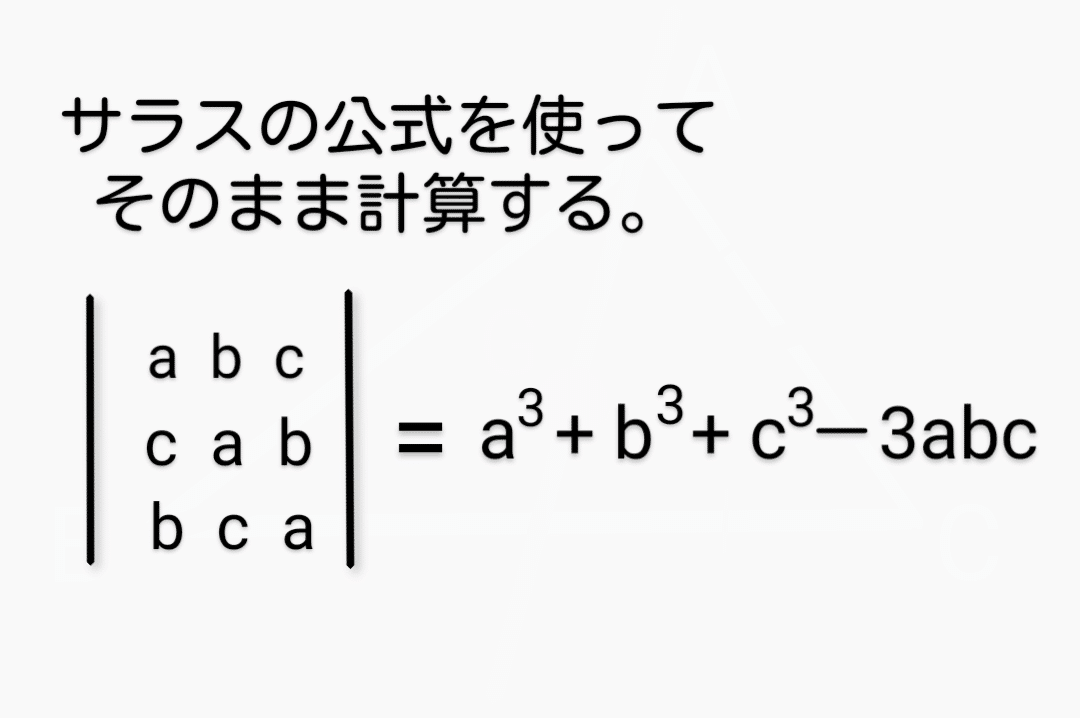
②行列式の性質を使って、少し変形してからサラスの公式を使う。

よって、

高校レベルの数学の公式だから行列式なんか使わなくても導けるが、行列式を使ったほうが楽かな?と思ったことがあるので書いてみた。
#行列式
#行列
#サラスの公式
#数学がすき
#学問への愛を語ろう
#エッセイ
#因数分解
#展開
#線形代数
#表記のメリット
#ヘッシアン
#ヤコビアン
#二行二列
#三行三列
#公式
#数学マガジン
いいなと思ったら応援しよう!

