
数学 | 72の法則の導き方を考えてみた
72の法則とは?
72の法則とは、元金が2倍になるときの金利とその年数を計算するときに用いられる計算法である。
実際には多少ズレるが、
簡易的な式として、
Y= 72➗X
としておよその年数を計算することができる。
具体的に言うと、
金利が2%のとき、上の式のXに「2」を代入すれば、
Y=72➗2=36 。
つまり金利が2%のときには、元金が2倍になるのに、およそ「36年」かかることがわかる。
金利が3%ならば、
Y=72➗3=24なので、
およそ「24年」かかることが分かる。

実際には上の式を満たすX(金利X%)とY(かかる年数)の関係だから、単純な「反比例」とはならないのだが、
Y=72➗X
として「近似値」を計算できるということである。
疑問
「図1」の式から
「Y=72➗X」という式がどのようにして導き出せるのか調べてみたが、説明が省略されている場合が多い。
そこで、自分なりに「図1の式」から、「Y=72➗X」の式を導き出してみようと思った。
⚠️間違っているかもしれないので、数学に自信のある方がいらっしゃったら、「査読」をお願いいたします😄。
下準備
n乗した式を、「二次式」で近似することを考える。
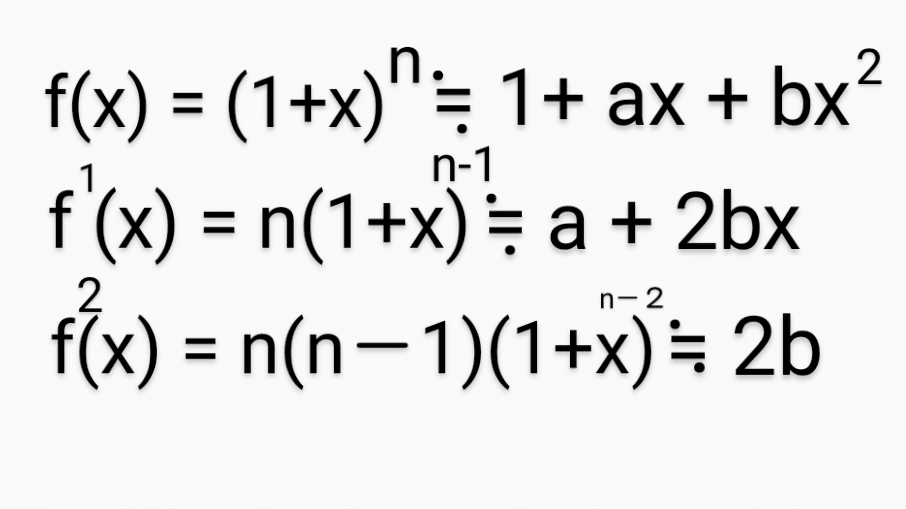
図2の2番目の式、3番目の式に
「X=0」を代入すれば、
n ≒ a
n(n-1) ≒ 2b
よって
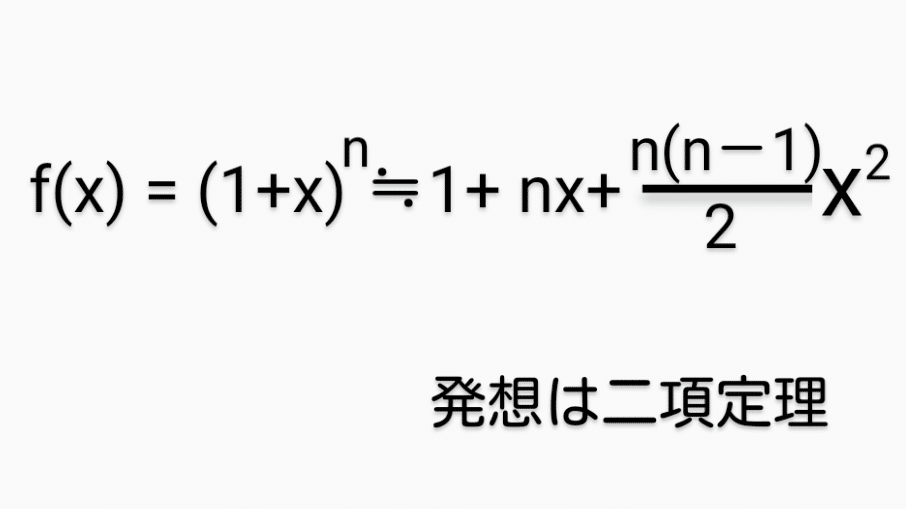
図3の式を
nをYに置き換える。
ただし
0<X<<1、Yは正の数とする。

図4の式の右辺を「=2」とおくと、

図5の式を計算して整理すると、

図6の式をYについての二次方程式として解くと、

ここで0<X<<1だから、
根号の中のXの3乗と、Xの4乗を
0と見なせば、
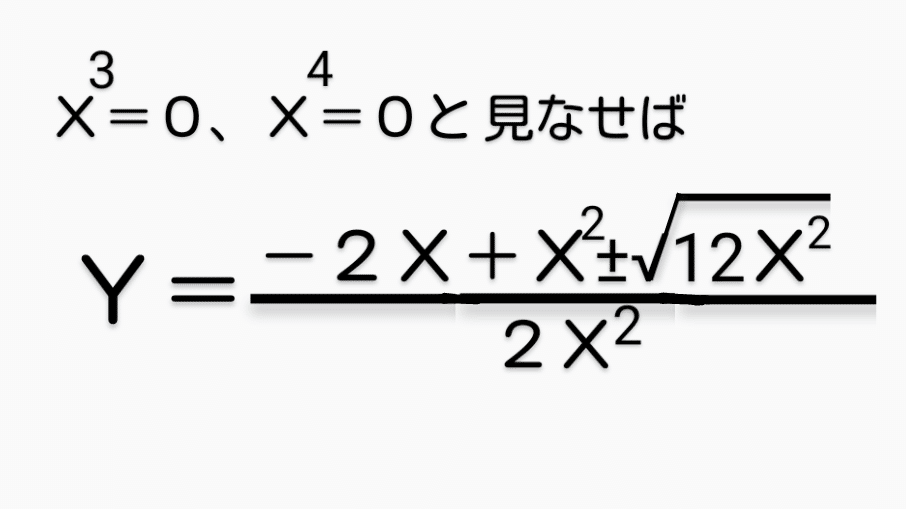
X>0だから、図8の式をもう少し整理すると、

図9の分子のXを0と見なして、
分母と分子を2で割ると、

Y>0だから、

出てきた😄
「あれっ?、72じゃない」と思った方もいるかもしれない。
結論を言えば、だいたいの年数がわかればよいので、「72」として計算しても「73」として計算しても大差はない。
ただ「72」のほうが、「約数」がたくさんあるので、暗算するには便利である、というだけの話である。
いいなと思ったら応援しよう!

