相関係数をベクトルで考えてみるお話

理工学分野の方に限らず、近年のデータサイエンスブームの影響もあり、「相関係数」という言葉は市民権を得ているような気がします。統計を少しでも勉強された方であれば「分散」や「標準偏差」といった言葉もご存知かもしれませんね。今回は相関係数の「値」が意味することをベクトルを使って“ゆるーく”紐解いてみたいと思います。

今回の内容を改めて勉強したい方は下記の岡太先生の本がとても参考になります。固有値、固有ベクトルといった重要な線形代数の内容についても、とても丁寧に記載されているので、これから「データ分析～多変量解析」に興味がある方のための数学の入門書としても大変おすすめです。

データ分析のための線形代数

2018年度日本行動計量学会の春合宿にて、岡太先生による「線形代数ブートキャンプ」なるものがありまして、その際にもテキストとして使用されたものです。岡太先生は、ベクトルの幾何学的意味をご説明される際に"粘土の塊"に"棒をぶっ刺しつつ"、「この時が1次独立で、この場合は1次従属になります」とニコニコしながら説明してくださりました。とても楽しい時間だったなぁ・・・。今年はコロナの影響で合宿が延期になったことが本当に悔やまれます。産総研の麻生先生の機械学習のお話を聞きたかったです。

日本行動計量学会　第22回春の合宿セミナー

そんな感傷に浸りつつ、ゆるーく説明していこうと思います。なんだか、今夜はそのような気分なのです。
(※ It's about 2500 words, so you'll be able to read it in 5 minutes. )

1. まずは改めて相関係数の式を見てみる

相関係数は、2つの変数間の直線的な関係の強さを表すものです。N個のデータにおける相関係数の式は下記のようになります。

rが1に近いほど、直線的であることを意味していることはご存知の方も多いはず。rの正負は分子で決まり(；分母は2乗しているので負にならない)、これにより点の分布の多い位置がわかります。これを図でイメージにすると下記のようになります。

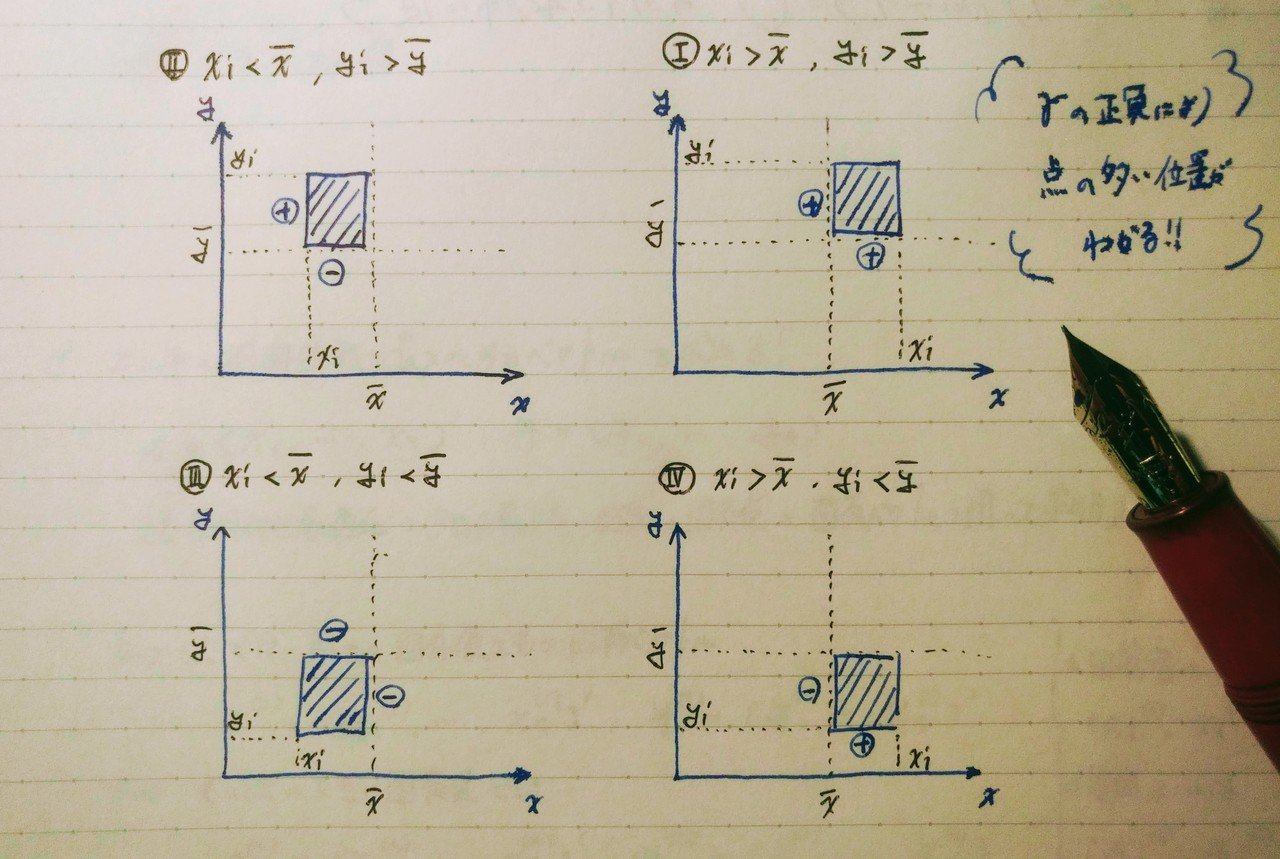
簡単にまとめると

xの平均とyの平均で4象限に仕切った時に・・・
→　rが「正」・・・右上Ⅰor左下Ⅲに点が多い
→　rが「負」・・・左上Ⅱor右下Ⅳに点が多い

ということになります。試しに少ない数のデータで相関係数を手計算してみます。

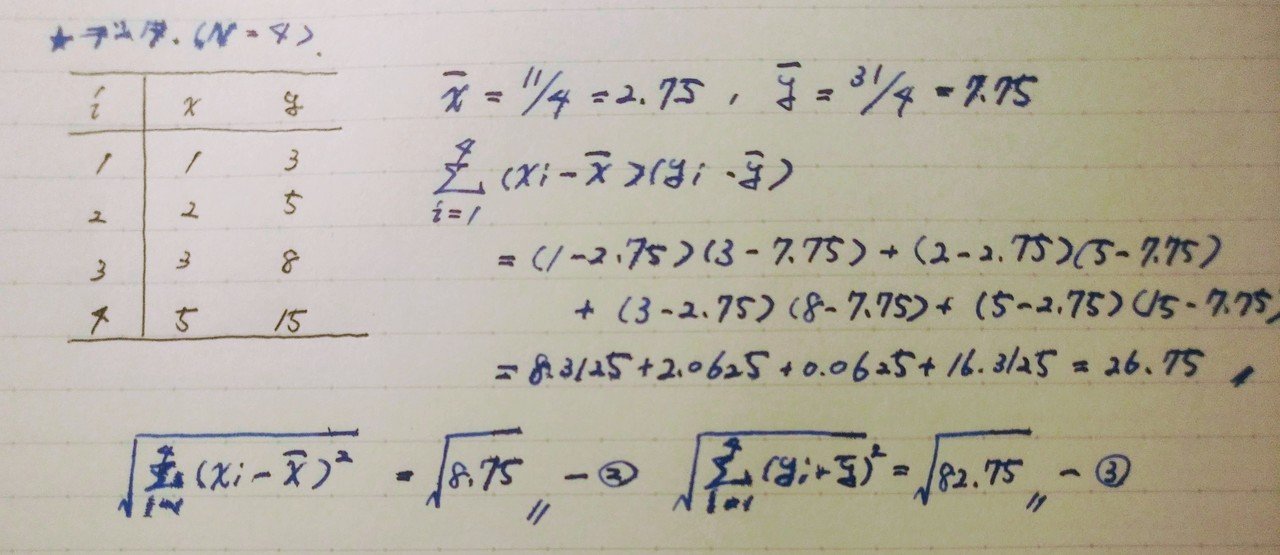
相関係数はr=0.994なので「正」かつ「1に近いので直線」であることがわかります。(手描きで)プロットして確認してみると・・・

確かにほぼ直線に並んでおり、平均で区切った時に第Ⅰ象限と第Ⅲ象限にプロットが集まっていますね。

ここまでで、相関係数の「正負」と「1に近いほど直線に並ぶ」ということについては、なんとなくわかった気がしますね。では相関係数の「値」ってどんな意味を持っているのでしょうか？この部分をベクトルを使って読み解いていきます。

2. ベクトルのおさらい

ご存知の方も多いかもしれませんが、念のためにベクトルのおさらいを簡単にしますね。エッセンスのみの線形代数スピードラーニング(？)です。

ちなみに、みなさんはベクトルを表す時はどのように記載していますか？矢印派？私は「アルファベットの中に棒を1本引いて、こいつぁ、太字だぜぃ！」派閥で10年近くお世話になっております。

(1) ベクトルの長さについて

(2) 2つのベクトルの内積について

内積については、グラフ上でベクトルを比較する(；幾何学的意味を考える)と少し面白いことがわかります。実はaに対して、近いもの(c、d、-aの順)ほど内積の値が大きく(5、-12、-13の順)なっています。すなわち、2つのベクトルの内積は、それらのベクトルがどの程度近いのかを表していると考えることができます。

しかし、これはベクトルの長さが同じ場合のみの話となります。例えば、上記のfは長さが5であり、aの√13と比べて長い場合においては、ベクトルの近さを表現できていないことがグラフよりもわかります。

そこで、ベクトルの近さを評価するには角度を見たほうがいいですね、となるわけです。

(3) 2つのベクトルのなす角度について

余弦定理を使うことで、2つのベクトルのなす角度を「ベクトルの長さ」と「ベクトルの内積」で表すことができましたね。θはアークコサインで求めてあげればわかるので、2つのベクトルのなす角度の求め方についても問題ないかと思います。

3. 相関係数の式と内積の式を見比べてみる

ここで、はじめに説明した相関係数の式と内積の式(；どちらかというと、ベクトルのなす角度の式)を見比べてみましょう。

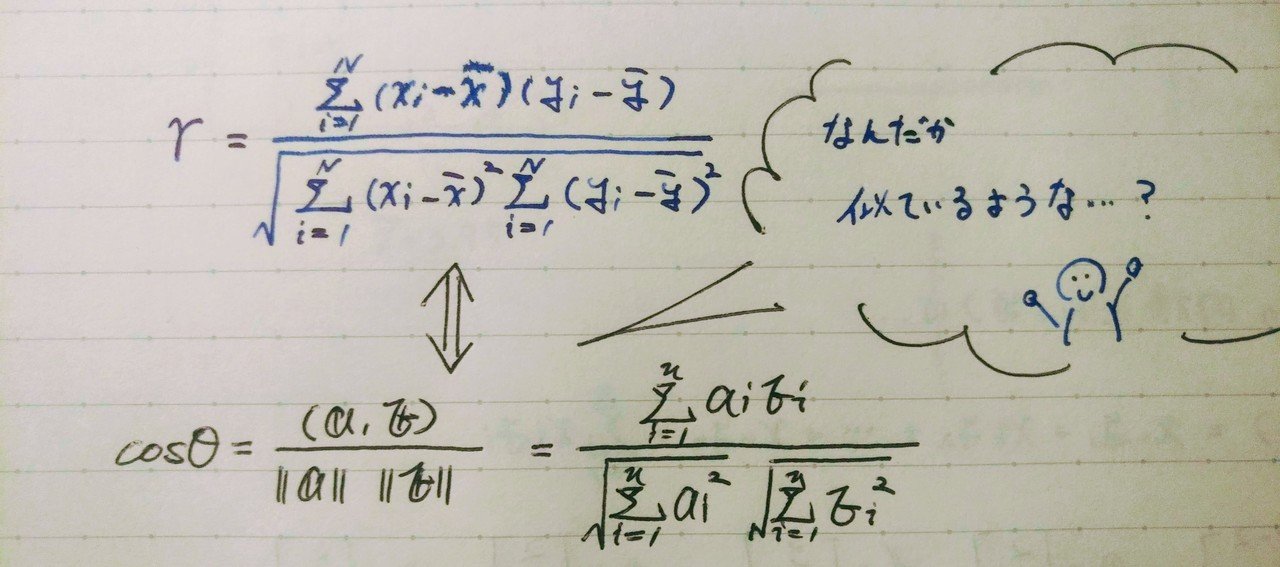
似ていますねぇ・・・。aiを(xi-x)、biを(yi-y)に置き換えたら同じになりますね。そうなんです、実は相関係数は内積の式のcosθとなっています。

この(xi-x)や(yi-y)は偏差行列と呼ばれ、平均からどの程度ズレているかを意味する行列です。従って、相関係数の正体は「平均からのズレを表した2つのベクトルのcosθ」となっているのです。

例えば、cosθは下記の表の値を取りますので、

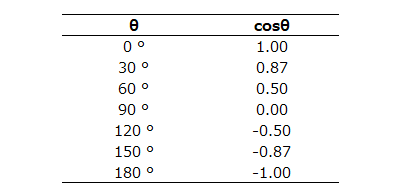
相関係数が1または-1の時というのは、2つのベクトルのなす角度が0°と180°の時を意味しており、一直線に並んでいることがわかります。一方で、2つのベクトルが最も離れている、すなわち直行している90°においては、cosθは0、つまり相関係数が0となるのです。

そのため、例えば「相関係数が0.25から0.50に2倍になった」というのは少し数字の捉え方としてはスジが悪い印象で、「相関係数が0.25はθ≒75°、0.50はθ=60°なので15°くらい近づいたんだな」と考える方が、数字を捉える感覚としては正しい気がします。

4. 結論

「今夜は、なぜか眠れないので線形代数な気分に・・・」(違うそうじゃない)

今回は相関係数の値のもつ意味をベクトルの内積の式を使って確認しました。偏差行列でできたベクトルの角度が相関係数ということでしたね。今後は「相関係数が○倍になった！？」というより、「あー、角度が近づいたんだなぁ」とひっそりと思うようにしてみてはいかがでしょうか。

以上、相関係数をベクトルで考えてみるお話でした。

----------------------------------------------------------

REFERENCE
[1] 岡太彬訓. データ分析のための線形代数. 共立出版, 2019, 26-54.

データ分析のための線形代数

「2019年の初版4刷」は合宿メンバー(100人くらい？)のための追加と聞いています。そのため、新品で手に入れた手元にあるこの本は、実は貴重な1冊なのかもしれません。