
信用創造という名の錬金術
みんなのやる気もあるしビジネス・チャンスもあるけれども、お金だけが無い町があります。その町に銀行はありますが、残念ながら預金はゼロです。預金さえあれば銀行はお金を貸し出せて、町にお金が回り始めます。ただし、銀行が貸し出せるのは、預金総額の90%までです。
そんな町の銀行にAさんが100万円預金したとしましょう。そうすると銀行は90万円をBさんに貸します。Bさんが90万円分の資材をCさんから購入して、Cさんは売って得た代金90万円を銀行に預けたとしましょう。そうすると銀行はその90%、すなわち81万円を新たに貸し出すことができます。
話はまだまだ続きます。銀行が誰かに81万円を貸し出せば、そのお金はやがて誰かが銀行に預けることになります。そうなると銀行はさらにその90%すなわち72万9千円を別の誰かに貸し出します。
実際には貸し出せる上限額を1人に貸し出すとは限りません。何人かに分けて貸し出す場合もあるでしょうけれど、需要が多ければ最終的には上限額の全額が貸し出されることになるでしょう。
また、現実には売って得たお金を全額預金するとも限りません。すぐに投資・消費することもあるでしょう。けれども中期的に見れば、お金は市中を回りながら、いずれかのタイミングで銀行に戻ってくると考えられます。
そう考えると、お金は銀行を経由しながら市中をぐるぐる回る間に、90%の90%の90%の・・・とだんだんと増えていくのです。
さて、ここで突然ですが、次の式を展開してください。
○ (1−r)(1+r+r²+…+rⁿ⁻¹) =[ ア ] (← r と n の式になりますね)
ここで 0<r<1 としましょう。そこで両辺を 1−r で割りましょう。
ところで、0<r<1 のとき rⁿ はどんどん小さくなって 0 に近づきますね。ということは、n を無限に大きくすると、
○ 1+r+r²+…+rⁿ+… =[ イ ] (← r だけの式です)
となるわけです。
はい、準備が整いました。では、ここで【問題】です。
○ 銀行が預金残高の90%を貸し出し続ける場合、銀行の預金総額は初めにAさんが預けた金額の何倍になるでしょうか?
◇ ◇ ◇
空欄[ア]と[イ]は高校数学で言うと数列の問題ですが、上のような【問題】の出し方もアリだと思うんですよ。つまり「公式を知らなかったらお手上げ」の形ばかりでなくて、問題に答えながら回答者が「なるほど、そういうことかっ!」と理解してくれるのも良いと思うのです。
では、《解説・解答》といきましょう。
最初の空欄[ア: 1−rⁿ ]は機械的に展開すれば出て来ます。
続いて問題文に書いてある通りに「両辺を 1−r で割って、さらに rⁿ=0 」とすれば空欄[イ: 1/(1−r) ]とわかります。もちろん公式を覚えていれば、そのまま書いてもOKです。
(1−r)(1+r+r²+…+rⁿ⁻¹) …
↓ この式を展開すると、
(1−r)(1+r+r²+…+rⁿ⁻¹) =1ーrⁿ
↓ 両辺を 1ーr で割って、
1+r+r²+…+rⁿ⁻¹=(1ーrⁿ)/(1ーr)
↓ 0<r<1 のとき rⁿ → 0 だから、
0<r<1 のとき 1+r+r²+…+rⁿ+… =1/(1ーr) が成り立ちます
そして最後に[ イ ]の式に r=0.9 を入れると・・・銀行の預金総額は初めにAさんが預けた金額の「 10倍 」になるんですね。
これが「信用創造 という名の錬金術」のカラクリです。いや、錬金術という言い方は不適切だったでしょうか。。。
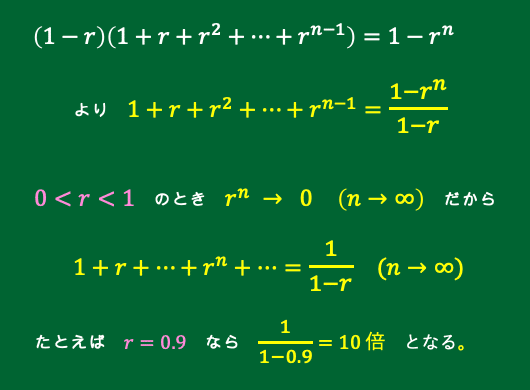
◇ ◇ ◇
〜 数学目線で社会を見る 〜
▷ 投票のパラドックス
▷ 信用創造という名の錬金術
▷ シェア・タクシーの割り勘定
